22. Децили и перцентили.

Децили – делят совокупность на 10 частей

D₁ = X_D1 + i *(∑f_i/10-∑f_D1-1)/f_D1

Перцентили – делят совокупность на 100 частей

P₁ = X_P1 + i *(∑f_i/100-∑f_P1-1)/f_P1

23. Основные показатели изменчивости.

I.Базовые показатели:

• Наименьшее значение

• 1-й квартиль

• Медиана

• 3-й квартиль

• Наибольшее значение

II. Абсолютные показатели:

1. Размах вариации

2. Среднее линейное отклонение

3. Среднее квадратическе отклонение

4. Дисперсия

24. Размах и среднее линейное отклонение.

Размах вариации – абсолютная разность между максимальным и минимальным значениями признака в изучаемой совокупности.

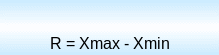
Среднее линейное отклонение

Простое:

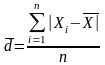
Взвешенное:

25. Простое и взвешенное стандартное отклонение (для выборки и гс).

Стандартное отклонение отражает типичное расстояние между средним значением и отдельным значением набора данных и показывает степень случайности в расположении отдельных значений относительно их среднего.

• Простое для выборки:

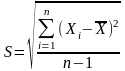
• Взвешенное для выборки:

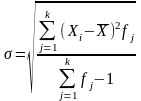
• Простое для генеральной совокупности:

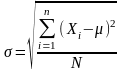
• Взвешенное для генеральной совокупности:

26. Дисперсия.

Дисперсия – мера рассеивания.

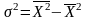
27. Относительные показатели изменчивости

• K оссилляции (относительный размах вариации)

V_r = R/(X|)*100%

• K вариации

V_s =S/(X|)*100% для выборки

V_ζ =ζ/(μ)*100% для генеральной совокупности

V_ζ<33% - совокупность однородная

• Стандартная ошибка среднего

S_x| =S/√n

Указывает, насколько среднее выборки X| отличается от среднего генеральной совокупности.

• Линейный коэффициент вариации

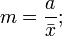
28. Основные параметры нормального распределения.

Нормальное распределение – теоретически гладкая гистограмма. Идеальный набор данных, в которых большинство чисел сконцентрировано в средней части диапазона значений.

Уравнение кривой, описывающей нормальное распределение

X| = Mo

2 основных параметра нормального распределения:

• Среднее анчение

• Стандартное отклонение

Вероятность того, что имеющее НР случайная величина принимает значение, лежащее в некотором интервале, равна площади под кривой НР между значениями, ограничивающими данный интервал.

Правило 3х сигма для нормального распределения:

29. Асимметрия.

Р азличают правостороннюю и левостороннюю асимметрии. Если As>0, то асимметрия правосторонняя, если As<0, то асимметрия левостороння.

30. Эксцесс.

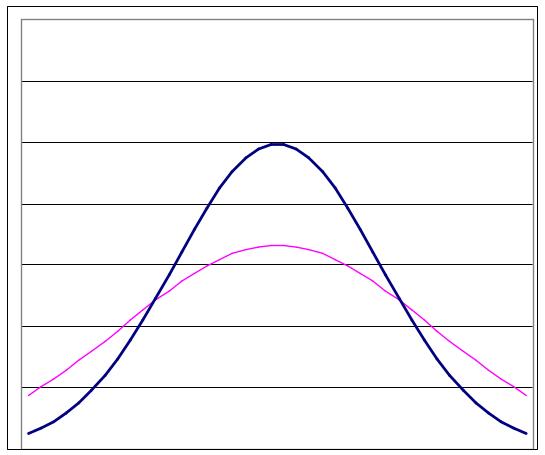
На графике верхний случай при Ex>0, средний при Ex=0, нижний при Ex<0.

Так же эксцесс называется моментом четвёртого порядка.

П ростая формула эксцесса:

В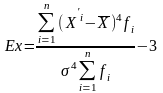 звешенная формула эксцесса:

31. Z-распределение.

Стандартизованная (Стандартная) теоретическая кривая НР.

X| = 0,

S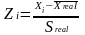 = 1.

Кривая НР симметрична относительно вертикальной оси

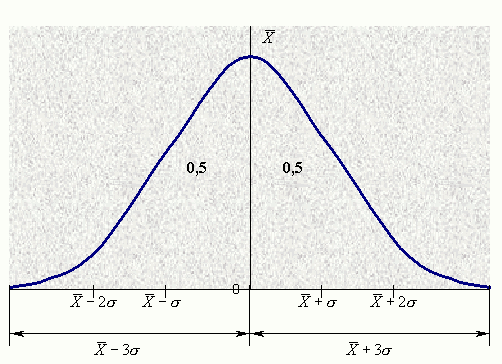
Таблица нормального распределения = таблица Z-значений

Значение z	Вероятность (того, что сл.вел.Z принимает значения < z
0,00 0,10 0,20 …	0,5000 0,5358 0,5793 …

Вероятность того, что сл.вел. Z принимает значения в интервале от 0 до z приведена в таблице Z-значений.

32. Стандартная ошибка среднего.

Стандартная ошибка среднего

S_x| =S/√n

Указывает, насколько среднее выборки X| отличается от среднего генеральной совокупности.