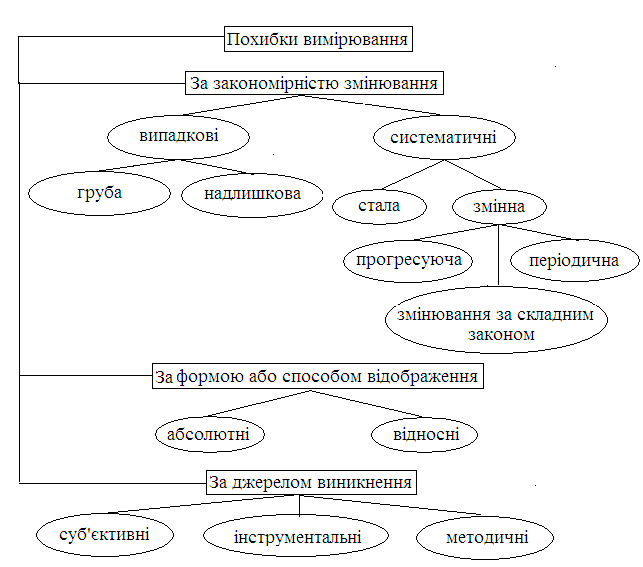
Різновиди похибок вимірювання

5 Частина

1. Випадкові похибки

2. випадкові похибки не піддаються виключенню з результатів вимірювань, то вплив на результат вимірювань з зводиться до вивчення властивостей сукупностей результатів окремих спостережень

3. Природа і фізичне суть випадкових і систематичних складових похибки вимірювань різна. Проте оцінки невиключених залишків систематичних похибок і випадкових похибок здійснюються на основі обробки статистичного матеріалу, що є сукупністю результатів вимірювань.

4. Для вивчення випадкових похибок використовуються методи теорії ймовірності і математичної статистики. Ці методи застосовні і для невиключених систематичних складових.

3. Дискретні і неперервні випадкові величини

4. Законом розподілу випадкової величини

5. Функція розподілу F(x)

6. Густиною імовірності безперервної випадкової величини

Функція розподілу F(x), як і ймовірність, є величина безрозмірна, а густина вірогідності має розмірність, зворотну розмірності випадкової величини.

Функція розподілу F(x) виражається через густину вірогідності φ(х)

7. Математичним очікуванням М (х) дискретної випадкової величини X

8. Математичним очікуванням М(х) безперервної випадкової величини X

Модою М_о(х) Одно- і двохмодальний розподіл ймовірності випадкової величини х

9. Для вивчення розподілу випадкових величин користуються рядом числових характеристик: міри положення і міри розсіювання.

10. До характеристик положення відносяться: математичне очікування, мода, медіана. Математичне очікування випадкової величини називають також середнім значенням випадкової величини.

11. Математичним очікуванням М (х) дискретної випадкової величини X називається сума добутків можливих значень її на відповідну ймовірність:

Математичним очікуванням М(х) безперервної випадкової величини X

11. Медіаною випадкової величини X

12. Геометрично медіана є абсцисою точки, яка ділить площу, обмежену кривою розподілу, пополам

13. Дисперсією D(x) дискретної випадкової величини Х

14. Середнєквадратичне відхилення випадкової величини

15. Середнєквадратичне відхилення вимірюється в тих же одиницях, що і сама величина Х і її середнє значення, тоді як дисперсія виражається в квадратах відповідної одиниці вимірювання

17. Четвертий центральний момент μ₃ визначає властивість гостроверхості кривої розподілу. За характеристику цієї властивості приймають безрозмірну величину τ, звану коефіцієнтом ексцесу

18. Міри розсіювання випадкової величини. дисперсія і середньоквадратичне відхилення.

19. Моментом ряду розподілу щодо початкового значення х = а називається сума добутків відхилень значень х_і від а в степені r на відповідну частоту:

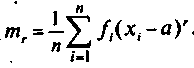
Розрізняють початкові(математичні очікування r –ї степені випадкової величини ) і центральні (математичні очікування r –ї степені відхилення випадкової величини від її математичного очікування) моменти r -го порядку.

21. Зa допомогою середнього квадратичного відхилення у можна оцінити ймовірність того, що при однократному спостереженні випадкова похибка Δ по абсолютному значенню не буде більшою від деякого наперед заданого значення ε . Це можна здійснити за допомогою нерівності П.Чебишева, яка має такий вигляд:

22. Перший центральний момент завжди =0, другий – дисперсія, третій – асиметрія, третій центральний момент μ₃ характеризує ступінь асиметрії кривої розподілу щодо математичного очікування, але для зручності за характеристику асиметрії приймають безрозмірну величину, звану коефіцієнтом асиметрії α: або _а=₃/ ³

асиметрія позитивна (α>0), якщо мода знаходиться ліворуч від середнього значення М(х), і негативна якщо мода знаходиться праворуч

23. Середнє квадратичне відхилення коефіцієнта асиметрії:

Розподіл можна вважати симетричним при виконанні умови:

24. аформула ексцесу Е=₄/ ^{4 .} Контр ексцес визначається:

При симетричному одномодальному розподілі ексцес звичайно позитивний (τ>0), якщо крива розподілу гостроверха, і негативний (τ<0), якщо крива розподілу плосковерха.