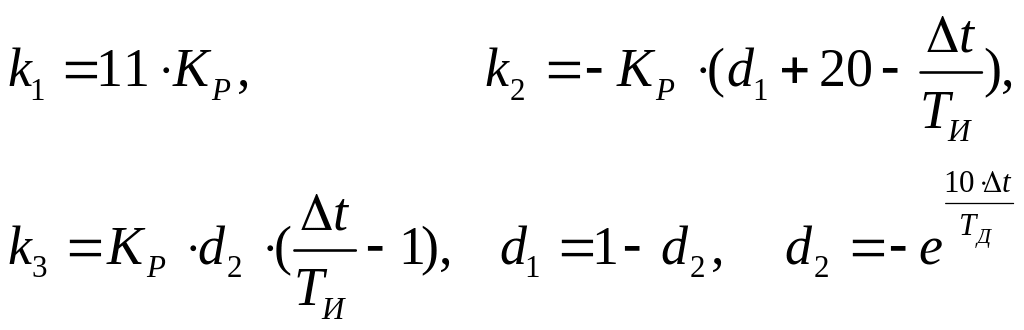- •Методические указания
- •Содержание
- •О дноконтурные системы регулирования
- •С истемы регулирования по инвариантной схеме
- •3. Системы регулирования по каскадной схеме
- •4. Системы многомерного управления. Общие сведения
- •6. Синтез системы управления для простейшего многомерного объекта
- •7. Синтез апериодического регулятора
- •8. Реализация управляющих воздействий
Министерство образования и науки Украины
Одесский национальный политехнический университет
Кафедра АТП
А.А.Стопакевич
Методические указания
по разработке систем управления промышленными технологическими процессами, заданными типовыми моделями
для подготовки к государственному экзамену по направлению
«Автоматизация и компьютерно – интегрированные технологии
Утверждены на заседании
кафедры АТП
7.11.2007, протокол №4
Одесса, 2008
Содержание
1. Одноконтурные системы регулирования 3
2. Системы регулирования по инвариантной схеме 4
3. Системы регулирования по каскадной схеме 6
4. Системы многомерного управления. Общие сведения 8
5. Синтез оптимального цифрового П-регулятора для
одномерного типового объекта 9
6. Синтез системы управления для простейшего многомерного объекта 10
7. Синтез апериодического регулятора 11
8. Реализация управляющих воздействий 11
О дноконтурные системы регулирования
Такие
системы проще всего проектируются по
методике Копеловича. Параметры настройки
регуляторов ПИД-семейства
![]() определяются
по типовой модели процесса и принятому
виду переходного процесса в соответствии
с таблицей, где
определяются
по типовой модели процесса и принятому
виду переходного процесса в соответствии
с таблицей, где
![]() – перерегулирование,
– перерегулирование,
![]() –
время регулирования,
–
время регулирования,
![]() ,
,
![]() ,
,
![]() .
.
Объект
|
, % |
П |
ПИ |
ПИД |
|||||
|
|
|
|
|
|
|
|
||
|
0 |
0.30 |
0.60 |
0.80 |
0.50 |
0.95 |
2.40 |
0 |
0.40 |
20 |
0.70 |
0.70 |
1.00 |
0.30 |
1.20 |
2.00 |
0 |
0.40 |
|
40 |
0.90 |
1.00 |
1.00 |
0.35 |
1.40 |
1.30 |
0 |
0.50 |
|
|
0 |
0.345 |
0.46 |
5.75 |
0 |
0.65 |
5.00 |
0 |
0.23 |
20 |
0.71 |
0.70 |
3.00 |
0 |
1.10 |
2.00 |
0 |
0.37 |
|
40 |
–– |
1.045 |
4.30 |
0 |
1.365 |
1.60 |
0 |
0.51 |
|
|
|
6Т |
4Т |
||||||
Параметры
настройки определяются,
если
![]() .
Если
.
Если
![]() ,
можно считать
,
можно считать
![]() и
определять настройки для безынерционного
объекта, основываясь непосредственно
на свойства типовых звеньев. Статическую
ошибку по заданию в П-регуляторе можно
убрать, введя компенсатор задания, т.е.
реализовав закон в виде
и
определять настройки для безынерционного
объекта, основываясь непосредственно
на свойства типовых звеньев. Статическую
ошибку по заданию в П-регуляторе можно
убрать, введя компенсатор задания, т.е.
реализовав закон в виде
![]() ,
,
![]() .
.
Уравнения регуляторов в цифровой форме имеют вид:
Закон |
Выражение в дискретном времени |
Пересчет коэффициентов |
П |
|
|
ПИ |
|
|
ПИД |
|
|
С истемы регулирования по инвариантной схеме
С истемы
проектируются на основе структурной
схемы, изображенной на рисунке. Для
разработки системы, обеспечивающей
независимость выхода объекта y
от возмущения f,
возмущение необходимо измерить и
пропустить через компенсатор с
передаточной функцией
истемы
проектируются на основе структурной
схемы, изображенной на рисунке. Для
разработки системы, обеспечивающей
независимость выхода объекта y
от возмущения f,
возмущение необходимо измерить и
пропустить через компенсатор с
передаточной функцией
![]() .
Используя известные правила
преобразования, получим вторую
структурную схему, откуда видно, что
условием инвариантности является
.
Используя известные правила
преобразования, получим вторую
структурную схему, откуда видно, что
условием инвариантности является
![]() ,
т.е.
,
т.е.
![]() .
.
Для типовых моделей, описываемых передаточными функциями инерционного (объект обозначен индексом 1) или интегрального (объект обозначен индексом 2) звена первого порядка с запаздыванием:
![]() ;
;
![]()
![]() ;
;
![]()
компенсатор
может быть описан передаточной функцией
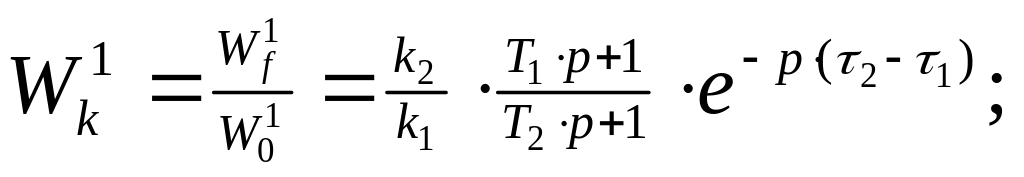
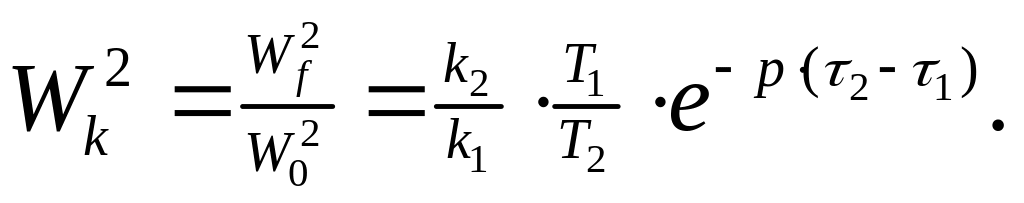
Ясно,
что компенсатор реализуем, если
![]()
Рассмотрим
вначале реализацию компенсатора
![]() .
Представив
в виде
.
Представив
в виде
![]()
![]() ,
можем записать.
,
можем записать.
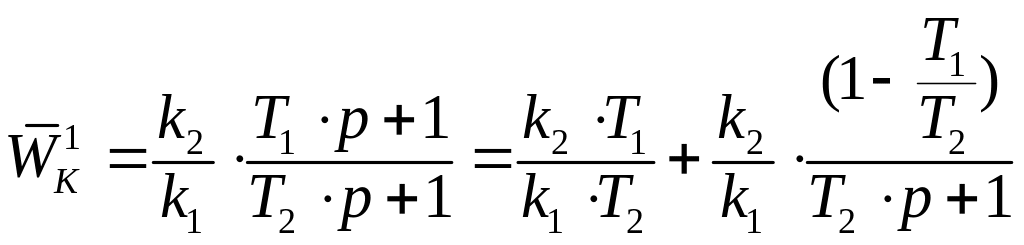 . Тогда, перейдя к дифференциальным
уравнениям,
. Тогда, перейдя к дифференциальным
уравнениям,
![]() ;
;
![]() ,
получим
,
получим
![]() ;
;
![]() ;
;![]() ;
;
![]() .
Выбрав период дискретизации
.
Выбрав период дискретизации
![]() таким
образом, чтобы
таким
образом, чтобы
![]() делилось
на
нацело,
делилось
на
нацело,
![]() (если
(если
![]() ,
то
,
то
![]() ),
перейдём к записи компенсатора в
дискретном времени
),
перейдём к записи компенсатора в
дискретном времени
![]() ;
;
![]() ,
где
,
где
![]() ;
;
![]() .
Для
упрощения реализации компенсатора
перейдём к матричной записи.
Нарисуем структурную схему
.
Для
упрощения реализации компенсатора
перейдём к матричной записи.
Нарисуем структурную схему
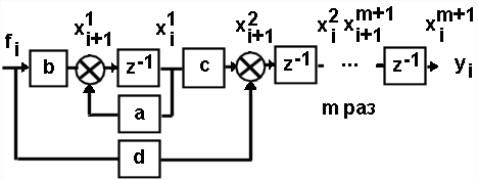
и по ней сразу запишем модель компенсатора в матричном виде
![]()
![]()
где
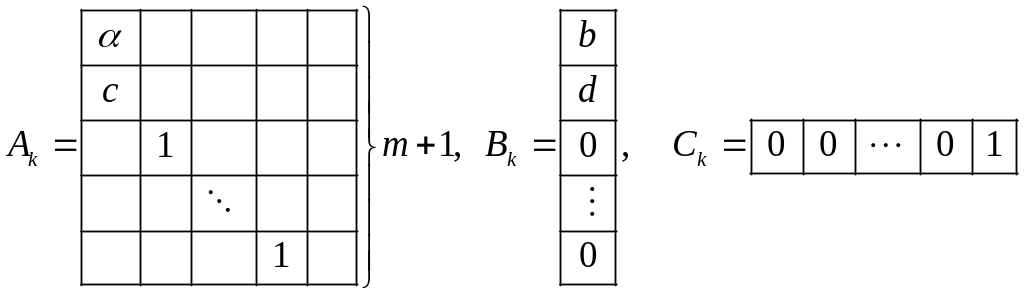 .
.
Предположив, что для стабилизации выбран ПИ-регулятор, программу реализации регулятора инвариантной системы с компенсатором измеряемых возмущений в случае пропорционального исполнительного механизма (пневматический, гидравлический, шаговый и т.д.) можно записать в виде
![]() ;
;
![]()
![]()
![]()
![]()
output(port,u–v);
Рассчитывая
компенсатор
![]() для
интегрального звена,
мы
можем записать систему в дискретном
времени
для
интегрального звена,
мы
можем записать систему в дискретном
времени
![]() ,
,
![]() ,
которой
соответствует структурная схема
,
которой
соответствует структурная схема
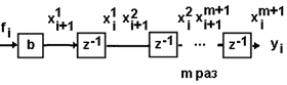
и матричная запись

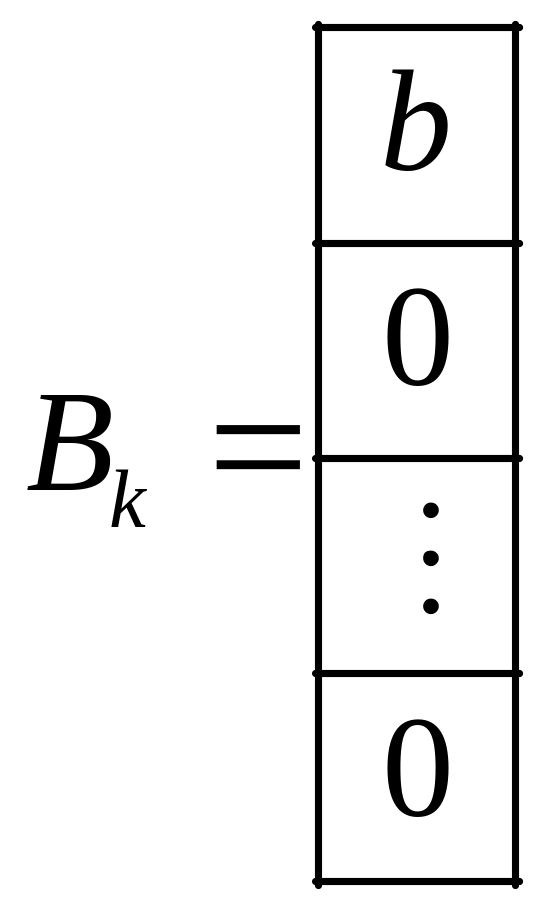
![]()
Выбрав для стабилизации П-регулятор, можем записать программу (для пропорционального ИМ)
![]()
![]() ;
;
![]() ;
;
![]() ;
;