Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский государственный энергетический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

vyshka.doc

Скачиваний:

Добавлен:

16.09.2019

Размер:

3.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

4.2.Производные первого порядка

Производная функции равна …

Функция задана в параметрическом виде Тогда производная первого порядка функции по переменной имеет вид …

Неявная функция определяется как решение уравнения . Тогда производная первого порядка при равна …

Функция задана в параметрическом виде Тогда производная первого порядка функции по переменной имеет вид …

Производная функции равна …

Функция задана в неявном виде Тогда производная первого порядка функции по переменной имеет вид …

Производная функции равна …

4.3.Асимптоты графика функции

Вертикальная асимптота графика функции задается уравнением вида …

Наклонная асимптота графика функции задается уравнением вида …

Вертикальная асимптота графика функции задается уравнением вида …

Наклонная асимптота графика функции задается уравнением вида …

, при

Вертикальная асимптота графика функции задается уравнением вида …

Горизонтальная асимптота графика функции задается уравнением вида …

Наклонная асимптота графика функции задается уравнением вида …

Горизонтальная асимптота графика функции задается уравнением вида …

4.4.Методы вычисления определенного интеграла

Определенный интеграл равен …

Несобственный интеграл …

равен

Несобственный интеграл …

равен

Определенный интеграл равен …

ДЕ 5. Функциональный анализ

5.1.Элементы теории множеств

Даны три множества: , и . Тогда число элементов множества равно …

Даны два множества: и . Тогда количество целых значений , принадлежащих пересечению множеств и , равно …

4 |

Даны множества: , . Тогда число целых чисел, принадлежащих их объединению равно …

Даны три множества: , и . Тогда число элементов множества равно …

Даны два множества: и . Тогда количество целых значений , принадлежащих объединению множеств и , равно …

8 |

Даны два множества: и . Тогда количество целых значений , принадлежащих разности множеств \ , равно …

Даны три множества: , и . Тогда число элементов множества равно …

Даны множества: и . Тогда число элементов, принадлежащих их пересечению равно …

3 |

5.2.Мера плоского множества

Плоская мера множества равна …

Мера плоского множества, изображенного на рисунке, равна …

Мера плоского множества равна …

Плоская мера множества равна …

Плоская мера отрезка [0; 1], лежащего на оси в плоскости равна …

Мера плоского множества равна …

Мера плоского множества , где А= и равна …

Мера плоского множества равна …

5.3.Отображение множеств

Биективное отображение отрезка на отрезок может быть задано функцией …

Отображение, действующее из отрезка на действительную числовую ось и имеющее обратное отображение, может быть задано функцией …

Пусть задано отображение . Тогда имеет вид …

Отображение действует по правилу: Тогда имеет вид …

Плоская мера множества равна …

Образом отрезка при отображении является отрезок …

Обратимым на является отображение …

Образом отрезка при отображении является отрезок …

Прообразом множества при отображении является …

Пусть задано отображение . Тогда представляет собой …

единичную окружность

Отображение действует по правилу: Тогда имеет вид …

Образом отрезка при отображении является отрезок …

5.4.Метрические пространства

Расстояние между точками и в метрике , где и , равно …

Функция , где – действительные числа, …

не удовлетворяет аксиоме симметрии

Функция заданная на множестве целых чисел …

удовлетворяет всем трем аксиомам метрического пространства

Расстояние между матрицами и в метрике равно …

Расстояние между функциями и пространства всех непрерывных действительных функций, определенных на отрезке , с метрикой , равно …

Функция , где и , …

не удовлетворяет аксиоме треугольника

Функция , заданная на множестве натуральных чисел …

удовлетворяет всем трем аксиомам метрического пространства

Расстояние между точками и в метрике , где и , равно …

Функция заданная на множестве целых чисел …

удовлетворяет всем трем аксиомам метрического пространства

Функция , где – действительные числа, …

удовлетворяет всем трем аксиомам метрического пространства

Функция , где – действительные числа, …

не удовлетворяет аксиоме симметрии

Не может служить метрикой пространства функция …

ДЕ 6. Комплексный анализ

6.1.Комплексные числа и их представление

Модуль комплексного числа равен …

Комплексное число задано в тригонометрической форме . Тогда его алгебраическая форма записи имеет вид …

Главное значение аргумента комплексного числа равно …

Комплексное число задано в показательной форме . Тогда его алгебраическая форма записи имеет вид …

Комплексное число задано в тригонометрической форме . Тогда его показательная форма записи имеет вид …

Тригонометрическая форма записи комплексного числа имеет вид …

Комплексное число задано в тригонометрической форме . Тогда его алгебраическая форма записи имеет вид …

Главное значение аргумента комплексного числа равно …

Комплексное число задано в показательной форме . Тогда его алгебраическая форма записи имеет вид …

Главное значение аргумента комплексного числа равно …

Показательная форма записи комплексного числа имеет вид …

6.2.Области на комплексной плоскости

Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: удовлетворяют условию …

Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …

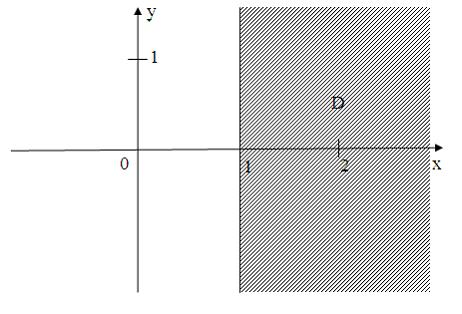Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке: Все точки комплексной плоскости, принадлежащие множеству , изображенному на рисунке, удовлетворяют условию …

6.3.Определение функции комплексного переменного

Если , то мнимая часть логарифма равна …

Дана функция . Тогда равно …

Если , то мнимая часть логарифма равна …

Дана функция . Тогда равно …

Если , то действительная часть логарифма равна …

Если , то мнимая часть логарифма равна …

Если и – комплексно-сопряженные числа, то мнимая часть функции при будет равна …

Если , то логарифм равен …

Если , то действительная часть логарифма равна …

Если и – комплексно-сопряженные числа, то мнимая часть функции , где , имеет вид …

Если и – комплексно-сопряженные числа, то действительная часть функции , при , будет равна …

Дана функция . Тогда равно …

Если , то действительная часть логарифма равна …

Если , то логарифм равен …

Если , то мнимая часть логарифма равна …

Если , то главное значение логарифма равно …

6.4.Особые точки функции комплексного переменного

Число особых точек функции равно …

Для функции точка является …

полюсом второго порядка

Для функции точка является …

полюсом второго порядка

Число особых точек функции равно …

Для функции точка является …

полюсом третьего порядка

Число особых точек функции равно …

Для функции точка является …

полюсом третьего порядка

Для функции точка является …

полюсом третьего порядка

ДЕ 7. Дифференциальные уравнения

Типы дифференциальных уравнений

Уравнение является …

линейным неоднородным дифференциальным уравнением первого порядка

Уравнение является …

уравнением с разделяющимися переменными

Уравнение является …

однородным относительно и дифференциальным уравнением первого порядка

Уравнение является …

уравнением с разделяющимися переменными

Уравнение является …

уравнением Бернулли

Уравнение является …

однородным относительно и дифференциальным уравнением первого порядка

Уравнение является …

линейным неоднородным дифференциальным уравнением первого порядка

Уравнение является …

уравнением в полных дифференциалах

Уравнение является …

дифференциальным уравнением первого порядка в полных дифференциалах

Уравнение является …

дифференциальным уравнением первого порядка в полных дифференциалах

Задача Коши для дифференциального уравнения первого порядка

Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …

Решение задачи Коши , имеет вид …

Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …

Функция является общим решением дифференциального уравнения 1-го порядка. Тогда для начального условия частное решение этого уравнения имеет вид …

Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …

Решение задачи Коши , имеет вид …

Частное решение дифференциального уравнения , удовлетворяющее условию , имеет вид …

Дифференциальные уравнения высших порядков, допускающие понижение

После понижения порядка дифференциальное уравнение приводится к виду …

Общий интеграл дифференциального уравнения при имеет вид …

Общее решение дифференциального уравнения имеет вид …

Частное решение дифференциального уравнения может иметь вид …

Общее решение дифференциального уравнения имеет вид …

Общее решение дифференциального уравнения при имеет вид …

Общее решение дифференциального уравнения имеет вид …

После понижения порядка дифференциальное уравнение приводится к виду …

Общее решение дифференциального уравнения имеет вид …

Системы двух линейных дифференциальных уравнений с постоянными коэффициентами

При решении системы дифференциальных уравнений можно получить уравнение второго порядка вида …

Общее решение системы дифференциальных уравнений имеет вид …

Решение задачи Коши , имеет вид …

Общее решение системы дифференциальных уравнений имеет вид …

Решение задачи Коши , имеет вид …

Общее решение системы дифференциальных уравнений имеет вид …

Решение задачи Коши , , имеет вид …

ДЕ 8. Теория вероятностей

Определение вероятности

Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – семь, а разность – три, равна …

В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет бракованных, равна …

Из урны, в которой находятся 6 черных шаров и 4 белых шара, вынимают одновременно 3 шара. Тогда вероятность того, что среди отобранных два шара будут черными, равна …

Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков – десять, равна …

Внутрь круга радиуса 4 наудачу брошена точка. Тогда вероятность того, что точка окажется вне вписанного в круг квадрата, равна …

Игральная кость бросается два раза. Тогда вероятность того, что сумма выпавших очков не меньше девяти, равна …

Из урны, в которой находятся 6 белых шаров и 4 черных шара, вынимают одновременно 4 шара. Тогда вероятность того, что среди отобранных 3 шара будут белыми, равна …

При наборе телефонного номера абонент забыл две последние цифры и набрал их наудачу, помня только, что эти цифры нечетные и разные. Тогда вероятность того, что номер набран правильно, равна …

В партии из 12 деталей имеется 5 бракованных. Наудачу отобраны три детали. Тогда вероятность того, что среди отобранных деталей нет годных, равна …

Полная вероятность. Формулы Байеса

В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 5 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет белым, равна …

0,47

Имеются четыре урны, содержащие по 3 белых и 7 черных шаров, и шесть урн, содержащих по 8 белых и 2 черных шара. Из наудачу взятой урны вытаскивается один шар, который оказался белым. Тогда вероятность того, что этот шар был вынут из первой серии урн, равна …

0,20

Банк выдает 70% всех кредитов юридическим лицам, а 30% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило юридическое лицо, равна …

0,875

Банк выдает 44% всех кредитов юридическим лицам, а 56% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,2; а для физического лица эта вероятность составляет 0,1. Тогда вероятность того, что очередной кредит будет погашен в срок, равна …

0,856

Банк выдает 40% всех кредитов юридическим лицам, а 60% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,1; а для физического лица эта вероятность составляет 0,05. Получено сообщение о невозврате кредита. Тогда вероятность того, что этот кредит не погасило физическое лицо, равна …

В первой урне 5 черных и 6 белых шаров. Во второй урне 3 белых шара и 6 черных шаров. Из первой урны переложили один шар во вторую урну. Тогда вероятность того, что шар, вынутый наудачу из второй урны, будет черным, равна …

В первой урне 3 черных шара и 7 белых шаров. Во второй урне 4 белых шара и 6 черных шаров. Из наудачу взятой урны вынули один шар, который оказался черным. Тогда вероятность того, что этот шар вынули из второй урны, равна …

Банк выдает 35% всех кредитов юридическим лицам, а 65% – физическим лицам. Вероятность того, что юридическое лицо не погасит в срок кредит, равна 0,15; а для физического лица эта вероятность составляет 0,1. Тогда вероятность непогашения в срок очередного кредита равна …

0,1175

Имеются три урны, содержащие по 5 белых и 5 черных шаров, и семь урн, содержащих по 6 белых и 4 черных шара. Из наудачу взятой урны вытаскивается один шар. Тогда вероятность того, что этот шар белый, равна …

0,57

Законы распределения вероятностей дискретных случайных величин

Дискретная случайная величина задана законом распределения вероятностей: Тогда ее функция распределения вероятностей имеет вид …

Банк выдал пять кредитов. Вероятность того, что кредит не будет погашен в срок, равна 0,1. Тогда вероятность того, что в срок не будут погашены три кредита, равна …

0,0081

Среднее число заявок, поступающих на предприятие бытового обслуживания за 1 час равно трем. Тогда вероятность того, что за два часа поступит пять заявок можно вычислить как …

Дискретная случайная величина задана законом распределения вероятностей: Тогда значения a и b могут быть равны …

Дискретная случайная величина задана функцией распределения вероятностей Тогда вероятность равна …

0,54

Для дискретной случайной величины : функция распределения вероятностей имеет вид: Тогда значение параметра может быть равно …

0,7

Дискретная случайная величина задана законом распределения вероятностей: Тогда вероятность равна …

0.5

0,655

Дискретная случайная величина задана законом распределения вероятностей: Тогда вероятность равна …

0,8

Числовые характеристики случайных величин

Дисперсия дискретной случайной величины , заданной законом распределения вероятностей: равна 0,06. Тогда значение равно …

1,5

Проводится n независимых испытаний, в каждом из которых вероятность появления события A постоянна и равна 0,6. Тогда математическое ожидание и дисперсия дискретной случайной величины X – числа появлений события A в проведенных испытаниях равны …

Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее дисперсия равна …

7,56

Непрерывная случайная величина задана плотностью распределения вероятностей . Тогда математическое ожидание a и среднее квадратическое отклонение этой случайной величины равны …

Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее математическое ожидание равно …

4,6

Дискретная случайная величина X задана законом распределения вероятностей: Тогда ее среднее квадратическое отклонение равно …

0,80

Математическое ожидание дискретной случайной величины , заданной законом распределения вероятностей: равно 4,4. Тогда значение вероятности равно …

0,7

Непрерывная случайная величина задана плотностью распределения вероятностей: Тогда ее дисперсия равна …

ДЕ 9. Математическая статистика

Статистическое распределение выборки

Из генеральной совокупности извлечена выборка объема , полигон относительных частот которой имеет вид: Тогда число вариант в выборке равно …

Из генеральной совокупности извлечена выборка объема , гистограмма частот которой имеет вид: Тогда значение a равно …

			38

Из генеральной совокупности извлечена выборка объема : Тогда значение равно …

Из генеральной совокупности извлечена выборка объема , полигон частот которой имеет вид: Тогда число вариант в выборке равно …

Из генеральной совокупности извлечена выборка объема , гистограмма относительных частот которой имеет вид Тогда значение a равно …

Из генеральной совокупности извлечена выборка объема : Тогда частота варианты в выборке равна …

Статистическое распределение выборки имеет вид Тогда значение относительной частоты равно …

0,25

Статистическое распределение выборки имеет вид Тогда объем выборки равен …

Точечные оценки параметров распределения

Если все варианты исходного вариационного ряда увеличить в два раза, то выборочная дисперсия …

увеличится в четыре раза

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 2,1; 2,3; ; 2,7; 2,9. Если несмещенная оценка математического ожидания равна 2,48, то равно …

2,4

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 15; 18; 21; 24. Тогда выборочная дисперсия равна …

11,25

В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты (в мм): 3,6; 3,8; 4,3. Тогда несмещенная оценка дисперсии равна …

0,13

Проведено пять измерений (без систематических ошибок) некоторой случайной величины (в мм): 4,5; 5,2; 6,1; 7,8, 8,3. Тогда несмещенная оценка математического ожидания равна …

6,38

Из генеральной совокупности извлечена выборка объема : Тогда выборочная дисперсия равна …

0,84

По выборке объема найдена выборочная дисперсия . Тогда исправленное среднее квадратическое отклонение равно …

2,0

Проведено четыре измерения (без систематических ошибок) некоторой случайной величины (в мм): 8, 9, , 12. Если несмещенная оценка математического ожидания равна 10, то выборочная дисперсия будет равна …

2,5

Из генеральной совокупности извлечена выборка объема : Тогда выборочное среднее квадратическое отклонение равно …

2,4

Интервальные оценки параметров распределения <

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении объема выборки этот доверительный интервал может принять вид …

Точечная оценка математического ожидания нормально распределенного количественного признака равна 12,04. Тогда его интервальная оценка с точностью 1,66 имеет вид …

Точечная оценка среднего квадратического отклонения нормально распределенного количественного признака равна 3,5. Тогда его интервальная оценка может иметь вид …

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении объема выборки этот доверительный интервал может принять вид …

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точность этой оценки равна …

1,12

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при увеличении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …

Точечная оценка вероятности биномиально распределенного количественного признака равна 0,38. Тогда его интервальная оценка может иметь вид …

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда при уменьшении надежности (доверительной вероятности) оценки доверительный интервал может принять вид …

Дан доверительный интервал для оценки математического ожидания нормально распределенного количественного признака. Тогда точечная оценка математического ожидания равна …

36,62

Точечная оценка математического ожидания нормально распределенного количественного признака равна 0,4. Тогда его интервальная оценка может иметь вид …

Проверка статистических гипотез

Двусторонняя критическая область может определяться из соотношения …

Правосторонняя критическая область может определяться из соотношения …

Основная гипотеза имеет вид . Тогда конкурирующей может являться гипотеза …

Соотношением вида можно определить …

правостороннюю критическую область

Для проверки нулевой гипотезы при заданном уровне значимости выдвинута конкурирующая гипотеза . Тогда область принятия гипотезы может иметь вид …

Соотношением вида можно определить …

левостороннюю критическую область

Соотношением вида можно определить …

двустороннюю критическую область

ДЕ 10

Отношения между множествами

Пусть некоторое бинарное отношение задается орграфом, изображенным на рисунке: Тогда это отношение является …

рефлексивным

Не является эквивалентным отношение …

включения множеств

Дано множество и бинарное отношение , и делит без остатка. Тогда количество элементов предикаты P равно …

Бинарное отношение задано на рисунке Тогда из трех матриц: ; ; соответствует матрице бинарного отношения матрица …

Даны множества и , тогда количество пар, удовлетворяющих бинарному отношению равно …

Бинарному отношению кратности элементов, заданному на множестве чисел соответствует орграф…

Бинарному отношению кратности элементов, заданному на множестве чисел соответствует матрица…

Симметричным бинарным отношением является отношение …

«слова x и y содержат одинаковое число букв»

Из трех предикатов отношений между множествами и : _,_,_, изображенным на рисунке является …

Операции над высказываниями

Отрицанием высказывания «Если я сдам зачет, то пойду в кафе с друзьями или на вечеринку» является высказывание:

«Я сдам зачет и не пойду ни в кафе с друзьями, ни на вечеринку»

Из трех логических выражений: эквивалентными являются …

На вопрос, кто из трех учащихся изучал логику, был получен правильный ответ: если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй. Тогда логику …

изучал третий учащийся

Для функции , заданной таблицей, СДНФ имеет вид …