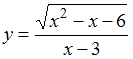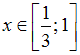3.3 Дифференциальная геометрия поверхностей

Первая квадратичная форма поверхности  имеет вид …

Точка с координатами  на поверхности  является …

гиперболической точкой

Уравнение касательной плоскости к прямому геликоиду  в точке  имеет вид …

Огибающая семейства сфер  имеет вид …

Вектор нормали  к поверхности гиперболического параболоида 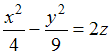 в точке  имеет координаты …

Точка с координатами  на поверхности  является …

гиперболической точкой

Вектор нормали  в точке  к поверхности тора 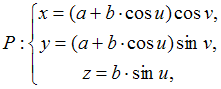 имеет координаты …

Вектор нормали  к прямому геликоиду  в точке  имеет вид …

Уравнение касательной плоскости к эллиптическому параболоиду  в точке  имеет вид …

Первая квадратичная форма поверхности 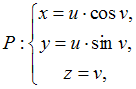 имеет вид …

3.4 Основные понятия топологии

Внешностью множества  в топологическом пространстве  с топологией  является …

пустое множество

Топологическая структура на множестве  задается множеством …

Внешностью множества  в топологическом пространстве  с топологией  является …

Внутренностью множества  в топологическом пространстве  с топологией  является …

Границей множества  в топологическом пространстве  с топологией  является …

Гомеоморфным к окружности является …

квадрат

Тривиальная топологическая структура на множестве  задается множеством …

Гомеоморфной к тору является …

«кружка с ручкой»

Внутренностью множества   в топологическом пространстве  с топологией  является …

пустое множество

ДЕ 4. Дифференциальное и интегральное исчисление

4.1 Область определения функции

Область определения вида  соответствует функции …

Область определения функции  имеет вид …

Область определения функции  имеет вид …

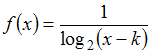Область определения функции  имеет вид . Тогда значение   равно …

5

Область определения функции  имеет вид …

Область определения функции  имеет вид …

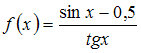Область определения функции  имеет вид …

Область определения функции  содержит интервал . Тогда значение параметра  может быть равно …

0,5

Область определения функции 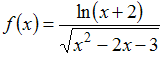 имеет вид …

Область определения функции 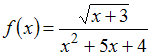 имеет вид …