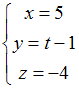2.2 Кривые второго порядка
Уравнением кривой
второго порядка
на
плоскости определяется …
|
|
|
эллипс |
Геометрическое
место точек, удаленных от плоскости
на
2 единицы, может иметь вид …
|
|
|
|
Мнимая полуось
гиперболы
равна
…
|
|
|
3 |
Расстояние между
фокусами гиперболы
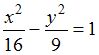равно
…
|
|
|
10 |
Центр окружности
имеет
координаты …
|
|
|
|
Соотношение
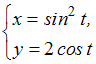в
прямоугольной декартовой системе
координат задает …
|
|
|
параболу |
Вершина параболы
имеет
координаты …
|
|
|
|
Уравнение директрисы
параболы, проходящей через точки
,
и
симметричной относительно оси
,
имеет вид …
|
|
|
|
Асимптоты гиперболы
задаются
уравнениями …
|
|
|
|
Радиус окружности
равен
…
|
|
|
2 |
2.3 Плоскость в пространстве
Плоскость, проходящая
через точки
и
параллельно
оси
,
задается уравнением …
|
|
|
|
Геометрическое место точек, удаленных от плоскости на 2 единицы, может иметь вид …
|
|
|
|
Общее уравнение
плоскости, проходящей через точку
параллельно
плоскости
,
имеет вид …
|
|
|
|
Уравнение плоскости,
проходящей через точку
параллельно
векторам
и
,
имеет вид …
|
|
|
|
Плоскость проходит
через точку
и
отсекает на осях абсцисс и ординат в
положительных направлениях отрезки
длины 3 и 5 соответственно. Тогда общее
уравнение плоскости имеет вид …
|
|
|
|
Нормальное уравнение
плоскости
имеет
вид …
|
|
|
|
Общее уравнение
плоскости, проходящей через точку
перпендикулярно
прямой
,
имеет вид …
|
|
|
|
Уравнение плоскости,
проходящей через точки
,
и
,
имеет вид …
|
|
|
|
Плоскости
и
перпендикулярны
при значении
,
равном …
|
|
|
|
2.4 Прямая линия в пространстве
Прямая
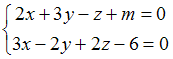пересекает
ось
при
значении параметра m,
равном …
|
|
|
– 4 |
Параметрические
уравнения прямой, параллельной оси
и
проходящей через точку
имеют
вид …
|
|
|
|
Даны прямая линия
,
заданная уравнением
,
и плоскость
,
заданная уравнением
.
Тогда прямая
…
|
|
|
параллельна
плоскости
|
Острый угол между
прямыми
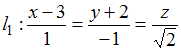и
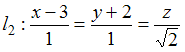равен
…
|
|
|
|
Точка пересечения
прямой
и
плоскости
имеет
координаты …
|
|
|
|
Прямая
параллельна
плоскости
,
если параметр
равен
…
|
|
|
– 11 |
Угол
между
прямой
и
плоскостью
равен
…
|
|
|
|
Каноническое
уравнение прямой, проходящей через
начало координат перпендикулярно прямым
и
,
имеет вид …
|
|
|
|
Каноническое
уравнение прямой
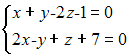может
иметь вид …
|
|
|
|
Расстояние между
прямой
и
плоскостью
равно
…
|
|
|
3 |
ДЕ 3. Дифференциальная геометрия