2. Общие требования к написанию расчетно-графической работы

Расчетно-графическая работа оформляется в соответствии с требованиями ГОСТов, ЕСКД и других стандартов и нормативных документов к текстовым документам и должно состоять из титульного листа, содержания, введения, последующих листов пояснительной записки и заканчиваться списком литературы, использованной студентом при выполнении работы. Все таблицы, схемы, рисунки, формулы и эскизы должны иметь наименование и нумерацию. При использовании справочной литературы необходима ссылка на нее.

3. Рекомендации по организации выполнения расчетно-графической работы

3.1 Рассмотрим пример выполнения расчетно-графической работы при следующей заданной выборке: 3,36; 3,38; 3,39; 3,39; 3,40; 3,40; 3,40; 3,42; 3,42; 3,42; 3,42; 3,42; 3,44; 3,44; 3,44; 3,46; 3,46; 3,47; 3,48; 3,50.

Разобьем выборку на 5 интервалов и определим величину интервала:

.

Занесем данные в таблицу 2.

Таблица 2 – Результаты наблюдений

х	3,36 – 3,388	3,388 – 3,416	3,416 – 3,444	3,444 – 3,472	3,472 – 3,50
Середина интервала	3,374	3,402	3,430	3,458	3,486
Частота	2	5	8	3	2

Вычисляем оценки и :

;

,

где коэффициент смещения (таблица 3).

Для графического определения вида закона распределения построим гистограмму. При построении разбиение на интервалы осуществляем таким образом, чтобы измеренные значения оказались серединами интервалов, что показано на рисунке 1.

Таблица 3 – Значения коэффициента в зависимости от количества наблюдений n

n	Mk	n	Mk	n	Mk
1	1,253	10	1,025	19	1,013
2	1,128	11	1,023	20	1,012
3	1,085	12	1,021	25	1,010
4	1,064	13	1,019	30	1,008
5	1,051	14	1,018	35	1,007
6	1,042	15	1,017	40	1,006
7	1,036	16	1,016	45	1,006
8	1,032	17	1,015	50	1,005
9	1,028	18	1,014	60	1,004

Рисунок 1 – Общий вид гистограммы

По виду гистограммы предположительно идентифицируем опытное распределение нормальным.

3.2 Определим содержит ли результат наблюдения х=3,50 грубую погрешность. Решим задачу с помощью критериев, установленных для нормального распределения.

1. Проверка по критерию "3σ". Вычислим удаленность подозрительного результата от центра распределения: .

Определим границу погрешности: .

Поскольку , то можно сделать вывод, что результат не содержит грубой погрешности.

2. Проверка по критерию Смирнова . Из таблицы 4 для принятого уровня значимости q =0,05 и объема выборки n=20 находим . Наличие грубой погрешности в результате х=3,50 не подтверждается, так как:

.

Таблица 4 – Квантили распределения β_k

Объем выборки	Предельное значение βk при уровне значимости q
	0,100	0,050	0,0010	0,005	0,001
1	1,282	1,645	2,326	2,576	3,090
2	1,632	1,955	2,575	2,807	3,290
3	1,818	2,121	2,712	2,935	3,403
4	1,943	2,234	2,806	3,023	3,481
5	2,036	2,319	2,877	3,090	3,540
6	2,111	2,386	2,934	3,143	3,588
7	2,172	2,442	2,981	3,188	3,628
8	2,224	2,490	3,022	3,227	3,662
9	2,269	2,531	3,057	3,260	3,692
10	2,309	2,568	3,089	3,290	3,719
15	2,457	2,705	3,207	3,402	3,820
20	2,559	2,799	3,289	3,480	3,890
25	2,635	2,870	3,351	3,539	3,944
30	2,696	2,928	3,402	3,587	3,988
40	2,792	3,015	3,480	3,662	4,054
50	2,860	3,082	3,541	3,716	4,108
100	3,076	3,285	3,723	3,892	4,263
250	3,339	3,534	3,946	3,946	4,465
500	3,528	3,703	4,108	4,263	4,607

3. Проверка по критерию Романовского. Определяем характеристики распределения без учета подозрительного результата ( ):

.

По таблице 5 находим коэффициент Стьюдента при объеме выборки и доверительной вероятности P = 0,95; . Наличие грубой погрешности подтверждается, т. к.:

.

Таблица 5 – Критерий Стьюдента (квантили Стьюдента)

Довери- тельная вероят- ность Р	Число степеней свободы k
	3	4	5	6	8	10	12	18	22	30	40	60	120
0,90	2,35	2,13	2,01	1,94	1,86	1,81	1,78	1,73	1,72	1,70	1,68	1,67	1,66	1,64
0,95	3,18	2,78	2,57	2,45	2,31	2,23	2,18	2,10	2,07	2,04	2,02	2,00	1,98	1,96
0,99	5,84	4,60	4,03	3,71	3,36	3,17	3,06	2,98	2,82	2,75	2,70	2,86	2,62	2,58

4. Проверка по критерию Шовене. При нахождении характеристик распределения участвуют все наблюдения и поэтому ; . Вычисляем квантиль z по формуле:

.

По таблице значений функции Лапласа [1] определяем вероятность выхода результатов за квантиль :

.

Тогда ожидаемое число наблюдений с результатом Ом:

.

Так как , то приходим к выводу об отсутствии грубой погрешности в результате наблюдения Ом.

5. Проверка по критерию Ирвина. Для полученных экспериментальных данных определяют коэффициент по формуле:

.

Затем этот коэффициент сравнивается с табличным значением , значения которого приведены в таблице 6. Т. к. , то нулевая гипотеза не подтверждается, т. е. результат не содержит грубой погрешности.

Таблица 6 – Критерий Ирвина

Число измерений n	Уровень значимости
2	2,8	3,7
3	2,2	2,9
10	1,5	2,0
20	1,3	1,8
30	1,2	1,7
50	1,1	1,6

6. Проверка по критерию вариационного размаха. Для его использования определяют размах вариационного ряда упорядоченной совокупности наблюдений :

.

Выполняем проверку по следующему неравентсву:

, (1)

где выборочное среднее арифметическое значение, вычисленное после исключения предполагаемого промаха (для );

критериальное значение (таблица 7).

Таблица 7 – Критерий вариационного размаха

	5	6	7	8 –9	10 –11	12 – 15	16 – 22	23 – 25	26 – 63
	1,7	1,6	1,5	1,4	1,3	1,2	1,1	1,0		0,9

Неравенство 1 выполняется: .

Таким образом, результат не содержит грубой погрешности.

7. Проверка по критерию Диксона. При использовании критерия вычисляют коэффициент Диксона (наблюдаемое значение критерия) для проверки наибольшего или наименьшего экстремального значения в зависимости от числа измерений. В таблице 8 приведены формулы для вычисления коэффициентов.

Для нашего случая: .

Таблица 8 – Формулы коэффициентов Диксона

Объем выборки	Коэффициент Диксона	Для наименьшего экстремального значения параметра	Для наибольшего экспериментального параметра
3 – 7
8 – 10
11 – 13
14 – 25

Таблица 9 – Критериальные значения коэффициентов Диксона (при принятом уровне значимости q)

Коэффициент Диксона	Число измерений	при уровне значимости
		0,1	0,05	0,02	0,01
	3 4 5 6 7	0,886 0,679 0,557 0,482 0,434	0,941 0,765 0,642 0,560 0,507	0,976 0,846 0,729 0,644 0,586	0,988 0,899 0,780 0,698 0,637
	8 9 10	0,479 0,441 0,409	0,554 0,512 0,477	0,631 0,587 0,551	0,683 0,636 0,597
	11 12 13	0,517 0,490 0,467	0,576 0,546 0,521	0,538 0,605 0,578	0,679 0,642 0,615
	14 15 16 17 18 19 20 21 22 23 24 25	0,462 0,472 0,452 0,438 0,424 0,412 0,401 0,391 0,382 0,374 0,367 0,360	0,546 0,525 0,507 0,490 0,475 0,462 0,450 0,440 0,430 0,421 0,413 0,406	0,602 0,579 0,559 0,542 0,527 0,514 0,502 0,491 0,481 0,472 0,464 0,457	0,641 0,616 0,595 0,577 0,561 0,547 0,535 0,524 0,514 0,505 0,497 0,489

Вычисленные для выборки по формулам значения коэффициентов Диксона сравнивают с принятым (табличным) значением критерия Диксона (таблица 9). Нулевая гипотеза об отсутствии грубой погрешности выполняется, если выполняется неравенство .

Если , то результат признается грубой погрешностью и исключается из дальнейшей обработки. В нашем случае: , т.е. грубая погрешность отсутствует.

Поскольку большинство критериев (6 из 7) показали отсутствие грубой погрешности, то результат наблюдения можно оставить в выборке.

3.3 Исключение систематических погрешностей измерений.

Если приведенные результаты представить графически, то можно увидеть на графике прогрессирующую, линейно возрастающую по модулю погрешность. График показан на рисунке 2.

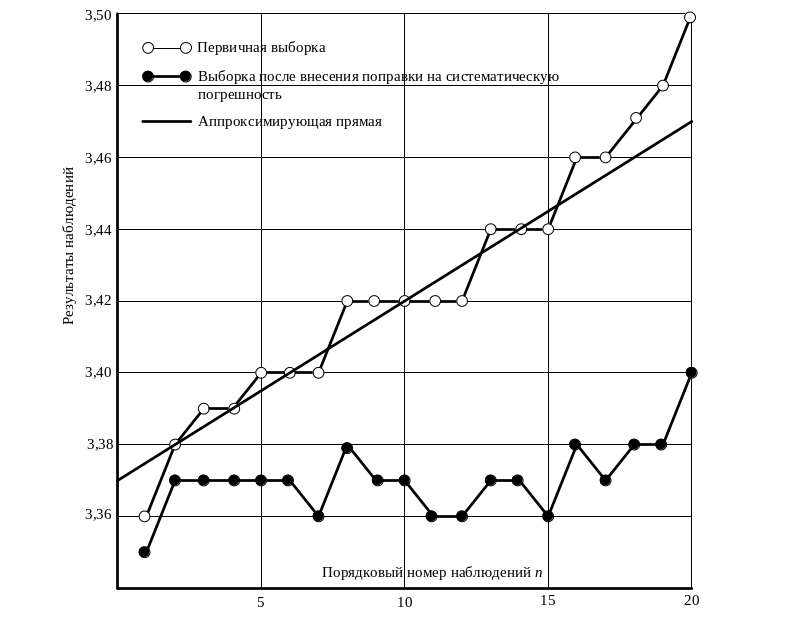
Рисунок 2 – Графическое представление результатов наблюдений

Модуль переменной составляющей систематической погрешности определяется по формуле:

, (2)

где разность между наибольшими и наименьшими значениями результатов наблюдений (по аппроксимирующей прямой);

общее число результатов;

порядковый номер измерения.

Разность определяется по аппроксимирующей прямой.

В данном примере , тогда .

Округлив значение до сотых долей (точность получения результатов), её исключают из результатов измерений, т. е.:

, (3)

где поправка, вносимая в каждый результат.

Как видно, поправка представляет собой погрешность, взятую с обратным знаком.

Систематическая погрешность, определенная по формуле 2 примет значения:

; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; .

Внеся исправления, получаем новую последовательность результатов: 3,35; 3,37; 3,37; 3,37; 3,37; 3,37; 3,36; 3,38; 3,37; 3,37; 3,36; 3,36; 3,37; 3,37; 3,36; 3,38; 3,37; 3,38; 3,38; 3,40.

3.4 Определения статистических функций распределения. Результаты (без исключения грубых и систематических погрешностей, после упорядочения и разбиения выборки на интервалы) представлены таблицей 10.

Таблица 10 – Промежуточные значения интервального ряда

Границы интервалов	Середины интервалов	Частота попадания в интервалы	Статистическая вероятность (частость)
3,36 – 3,388	3,374	2	0,10
3,388 – 3,416	3,402	5	0,25
3,416 – 3,444	3,430	8	0,40
3,444 – 3,472	3,458	3	0,15
3,472 – 3,50	3,486	2	0,10
		20	1,0

Представим заданный статистический ряд в виде гистограммы, показанной на рисунке 3.

Рисунок 3 – Гистограмма результатов измерений

Определенные ранее среднеарифметическое и среднеквадратическое отклонения равны:

; .

Вычислим дифференциальную функцию распределения для середин интервалов. Для этого вычислим значение нормированного аргумента по формуле для каждого интервала и занесем в таблицу 11:

. (4)

А затем, пользуясь статистической таблицей [1], определим дифференциальную функцию .

Таблица 11 – Вероятностные параметры распределения

Середины интервалов	,
3,374	-1,392;1,392	0,1415	0,1071	0,0823	0,10
3,402	-0,635;0,635	0,3156	0,2388	0,2628	0,35
3,430	0,122	0,3924	0,2970	0,5478	0,75
3,458	0,878	0,2636	0,1995	0,8106	0,90
3,486	1,635	0,1002	0,0758	0,9489	1,0

Используя свойство нормального распределения , находим значения дифференциальной функции в выбранных единицах. В случае использования интервалов применяют зависимость:

, (5)

где h – ширина интервала, в нашем случае она равна 0,028.

Значения нормальной функции распределения находятся по таблице [2] или по формуле:

.

Для построения статистической функции распределения можно воспользоваться формулой для дополнительных вычислений:

. (6)

;

;

;

;

;

.

Графики экспериментальной и теоретической функции интегрального вида показаны на рисунке 4.

По виду статистических кривых можно также сделать заключение о нормальности распределения экспериментальных данных, хотя для окончательного заключения требуется проверка по критериям согласия (или приближенная идентификация по точечным числовым характеристикам).

Рисунок 4 – Кривые интегральной функции распределений

3.5 При малых объемах выборки для проверки согласия опытного распределения с нормальным применяется составной критерий d. По заданным условиям уровень значимости .

Вычисляем выборочное среднее арифметическое X, несмещенную и смещенную оценки СКО:

Ом;

Ом;

Ом.

Проверяем согласие по критерию 1. Для этого определяем значение d:

Ом.

При n =20; ; из таблицы 12 находим квантили распределения d (после интерполяции):

; .

Гипотеза о нормальности распределения по критерию 1, при выбранном уровне значимости подтверждается, так как:

;

или

.

Проверка по критерию 2. По таблицам 13, 14 находим значения ; ; , т. е. находим произведение и сравниваем его с максимальным отклонением. Гипотеза о нормальности распределения по критерию 2 справедлива, так как в выборке нет ни одной разницы, превышающей значение:

.

Таким образом, гипотеза о нормальности закона опытного распределения по обоим критериям подтверждается при принятом уровне значимости .

Таблица 12 – Квантили распределения статистики d

11	0,9359	0,9073	0,8899	0,7409	0,7153	0,6675
16	0,9137	0,8884	0,8733	0,7452	0,7236	0,6829
21	0,9001	0,8768	0,8631	0,7495	0,7304	0,6950
26	0,8901	0,8625	0,8570	0,7530	0,7360	0,7040
31	0,8827	0,8625	0,8511	0,7559	0,7404	0,7110
36	0,8769	0,8578	0,8468	0,7583	0,7440	0,7167
41	0,8722	0,8540	0,8436	0,7604	0,7470	0,7216
46	0,8682	0,8508	0,8409	0,7621	0,7496	0,7256
51	0,8648	0,8481	0,8385	0,7636	0,7518	0,7291

Таблица 13 – Квантили интегральной функции Лапласа

Р	0,90	0,95	0,96	0,97	0,98	0,99
	1,65	1,96	2,06	2,17	2,33	2,58

Таблица 14 – Значения и , соответствующие различным и

		при уровне значимости равном
		0,01	0,02	0,05
10	1	0,98	0,98	0,96
11 – 14	1	0,99	0,98	0,97
15 – 20	1	0,99	0,99	0,98
21 – 22	2	0,98	0,97	0,96
23 – 27	2	0,98	0,98	0,97
28 – 32	2	0,99	0,98	0,97
33 – 35	2	0,99	0,98	0,98
36 – 49	2	0,99	0,99	0,98

3.6 Проверим с помощью критерия гипотезу о нормальном законе распределения погрешностей в указанном эксперименте.

Расположим экспериментальные данные в порядке возрастания: 3,36; 3,38; 3,39; 3,39; 3,40; 3,40; 3,40; 3,42; 3,42; 3,42; 3,42; 3,42; 3,44; 3,44; 3,44; 3,46; 3,46; 3,47; 3,48; 3,50.

Вычисляем значение величины :

.

3. Вычисляют значение величины :

, (7)

где значения коэффициентов берутся из таблицы 15.

Т. к. формула 7 примет следующий вид:

.

Коэффициенты , взятые из таблицы 15, имеют следующие значения:

; ; ; ; ; ; ; ; .

.

Находим расчетное значение критерия:

.

При определенном уровне значимости q (q=0,05) проверяем выполнение условия:

, (8)

где критическое значение критерия, взятое из таблицы 16.

.

По критерию условие (8) выполнено. Следовательно, гипотеза о нормальном распределении подтвердилась.

Таблица 15 – Значение коэффициентов

	3	4		5		6		7		8		9		10		11
k k-1 k-2 k-3 k-4	0,7071	0,6872 0,1677		0,6646 0,2413		0,6431 0,2806 0,0875		0,6233 0,3031 0,1401		0,6052 0,3164 0,1743 0,0561		0,5888 0,3244 0,1976 0,0947		0,5739 0,3291 0,2141 0,1224 0,0399		0,5601 0,3315 0,2260 0,1429 0,0695
	12		13		14		15		16		17		18		19		20
k k-1 k-2 k-3 k-4 k-5 k-6 k-7 k-8 k-9	0,5475 0,3325 0,2347 0,1586 0,0922 0,0303		0,5359 0,3325 0,2412 0,1707 0,1099 0,0539		0,5251 0,3318 0,2460 0,1802 0,1240 0,0727 0,0240		0,5150 0,3306 0,2495 0,1878 0,1353 0,0880 0,0433		0,5056 0,3290 0,2521 0,1939 0,1447 0,1005 0,0593 0,0196		0,4996 0,3234 0,2498 0,1902 0,1402 0,0987 0,0545 0,0182		0,4982 0,3206 0,2456 0,1876 0,1378 0,0954 0,0516 0,0174 0,0054		0,4964 0,3178 0,2412 0,1851 0,1336 0,0911 0,0476 0,0168 0,0034		0,4942 0,3154 0,2387 0,1828 0,1304 0,0876 0,0436 0,0152 0,0022 0,0008

Таблица 16 – Критические значения критерия

	Уровень значимости
	0,01	0,02	0,05
3	0,753	0,756	0,767
4	0,687	0,707	0,748
5	0,686	0,715	0,762
6	0,713	0,743	0,788
7	0,730	0,760	0,803
8	0,749	0,778	0,818
9	0,764	0,791	0,829
10	0,781	0,806	0,842
11	0,792	0,817	0.850
12	0,805	0,828	0,859
13	0,814	0.837	0,866
14	0,825	0,846	0,874
15	0.835	0,855	0,881
16	0,844	0,863	0,887
17	0,853	0,870	0,893
18	0,862	0,878	0,899
19	0,874	0,885	0,906
20	0,881	0,894	0,911

Таблица 17 – Календарный план выполнения расчетно-графической работы

Номер этапа	Содержание этапов работы	Процент выполнения	Срок выполнения, неделя семестра
1	Выдача задания	-	1
2	Анализ исходных данных задания. Подбор литературы.	5	3
3	Расчет характеристик выборки	30	4
4	Определение грубых погрешностей	40	5
5	Заключение о влиянии грубых погрешностей	45	6
6	Исключение систематических погрешностей измерений	50	7
7	Статистический анализ	60	8
8	Построение зависимостей	80	9
9	Проверка статистических расчетов при помощи критерия d.	90	10
10	Сдача расчетно-графической работы на проверку	100	11
11	Защита.		12