
- •1. Системи лінійних алгебраїчних рівнянь, сумісні і несумісні.
- •3. Матричний метод розв`язання.
- •2. Метод Крамера.
- •4. Метод Гауса.
- •5. Системи m лінійних рівнянь з n невідомими. Критерій сумісності системи. Теорема Кронекера-Капеллі.
- •6. Поняття функції. Області визначення і значення. Способи завдання функції.
- •7. Деякі властивості функції (монотонність, парність, періодичність), приклади.
- •8. Елементарні функції та їх класифікація.
- •9. Основні елементарні функції. Їх властивості, графіки.
- •10. Границя функції при х прямує до нескінченності.
- •11. Означення границя функції на мові "ε-δ". Геометричний зміст границі.
- •12. Означення границі функції на мові "послідовностей".
- •31. Вгнутість (випуклість) графіка функції. Геометричне пояснення. Необхідна і достатня умова вгнутості (випуклості) графіка функції.
- •32. Точки перегину. Необхідна і достатня умови перегину.
- •33. Асимптоти графіка функції. Приклади.
- •34. Повна схема дослідження функції.
31. Вгнутість (випуклість) графіка функції. Геометричне пояснення. Необхідна і достатня умова вгнутості (випуклості) графіка функції.
Крива у = f(х) називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.
Крива у = f(х) називається вгнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.
Н а
рис. крива у
— f(х)
опукла
на інтервалі (а;
b),
вгнута
на інтервалі (b;
с) і точка
В—
точка перегину.
а
рис. крива у
— f(х)
опукла
на інтервалі (а;
b),
вгнута
на інтервалі (b;
с) і точка
В—
точка перегину.
Теорема: Нехай функція у = f(х) є двічі диференційованою на (а; b), тоді:
1) якщо f" (х) < 0, х є (а; b), то крива у = f (х) опукла на (а; b);
2) якщо f" (х) > 0, х є (а; b), то крива у = f(х) вгнута на (а; b);
32. Точки перегину. Необхідна і достатня умови перегину.
Точкою перегину називається така точка кривої, яка відділяє її опуклу частину від вгнутої.
Необхідна умова існування точки перегину: якщо М0(х0; f(x0))— точка перегину графіка функції y=fx, то x0 — критична точка 2-го порядку.
Достатня умова існування точки перегину: якщо для функції fx точка x0 є критичною точкою 2-го порядку, і, переходячи через цю точку, друга похідна fx міняє знак, то точка x0 є точкою перегину функції f x.
33. Асимптоти графіка функції. Приклади.
Пряма називається асимптотою кривої, якщо відстань б від змінної точки М кривої до цієї прямої прямує до нуля, коли точка М, рухаючись по кривій, віддаляється на нескінченність.
Н а
рис. показано вертикальну (а), горизонтальну
(б)
і похилу
(в) асимптоти.
а
рис. показано вертикальну (а), горизонтальну
(б)
і похилу
(в) асимптоти.
З означення
асимптоти випливає, що для існування
вертикальної асимптоти х
= х0
необхідно
і достатньо, щоб
![]() .
.
Рівняння
похилої асимптоти будемо шукати у
вигляді у
= kх
+ b.
![]() ,
,
![]() Якщо
хоча б одна з границь не існує, або
дорівнює нескінченності, то крива
похилої асимптоти не має.
Якщо
хоча б одна з границь не існує, або
дорівнює нескінченності, то крива
похилої асимптоти не має.
34. Повна схема дослідження функції.
План цього дослідження наступний:
1) знаходять область визначення функції;
2) визначають точки розривів функції та їх характер;
3) знаходять корені функції;
4) визначають парність або непарність функції;
5) перевіряють функцію на періодичність;
6) обчислюють похідну функції, знаходять її критичні точки, знаходять інтервали монотонності і екстремуми;
7) обчислюють другу похідну функції і по ній визначають інтервали опуклості, угнутості і точки перегину;
8) знаходять асимптоти функції;
9) за отриманими даними будують якісний графік досліджуваної функції.
35. Поняття первісної. Приклади. Теорема про множину первісних для однієї функції.

36. Поняття невизначеного інтеграла та його властивості.
Множина всіх первісних заданої функції на заданому проміжку називається невизначеним інтегралом. Функція називається підінтегральною функцією, аргумент функції називається змінною інтегрування.
Властивості:


3 7.
Основні методи інтегрування. Приклади.
7.
Основні методи інтегрування. Приклади.
1. Безпосереднє інтегрування. Для розв’язання наступних прикладів будемо користуватись таблицею інтегралів, властивостями інтегралів і формулами з елементарної математики.


38. Визначений інтеграл. Інтегральна сума. Властивості.
Визначений інтеграл —це інтеграл функції з вказаною областю інтегрування.








72-2




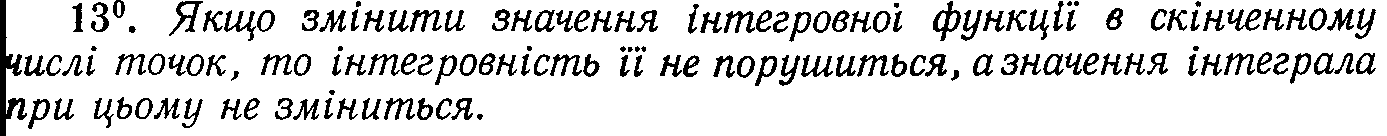
39. Інтеграл із змінною верхньою границею. Похідна інтеграла по верхній границі. Формула Ньютона-Лейбніца.


40. Формули інтегрування частинами та заміни змінної у визначеному інтегралі..





41. Геометричне застосування визначеного інтеграла. Приклади



Невласні інтеграли. Приклади



