1. Системи лінійних алгебраїчних рівнянь, сумісні і несумісні.

Систему m рівнянь з n невідомими вигляду

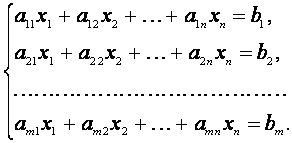
називають системою лінійних алгебраїчних рівнянь (СЛАР). Тут x 1 , x 2 , …, x n – невідомі; a ij – задані коефіцієнти (i=1, 2, …, m, j=1, 2, …, n); b 1 ,b 2 , …, b n – вільні члени системи.

Розв’язати систему (3.1) – значить знайти такі значення невідомих …, при підстановці яких у систему (3.1) усі її рівняння обертаються у тотожність.

Систему рівнянь називають сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку. Сумісну систему називають визначеною, якщо вона має один-єдиний розв’язок, і невизначеною, якщо вона має більше одного розв’язку.

3. Матричний метод розв`язання.

Використовуючи поняття добутку матриці на матрицю, систему можна записати у вигляді:

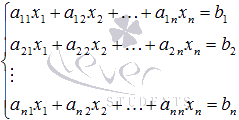
Які в матричній формі записуються так де,

основна матриця системи, 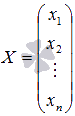матриця стовбець невідомих

матриця вільних членів.

2. Метод Крамера.

Для системи лінійних рівнянь з невідомими (над довільним полем)

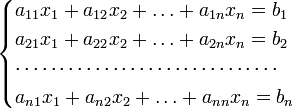
з визначником матриці системи , що не рівний нулю, розв'язок записується у такому вигляді:

(i-й стовпчик матриці системи замінюється стовпчиком вільних членів).

Іншим чином правило Крамера формулюється так: для будь-яких коефіцієнтів c1, c2, …, cn виконується рівність:

У такій формі формула Крамера справедлива без припущення, що не рівне нулю, не треба навіть, аби коефіцієнти системи були елементами цілісного кільця (визначник системи навіть може бути дільником нуля у кільці коефіцієнтів). Також можна вважати, що або набори та , або набір складаються не з елементів кільця коефіциєнтів системи, а деякого модуля над цим кільцем.

4. Метод Гауса.

Процес рішення за методом Гауса складається з двох етапів. На першому етапі (прямий хід) система приводиться до східчастого увазі:

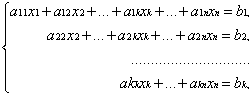де k n, aii 0, i = , АII - головний елемент системи.

На другому етапі (зворотний хід) йде послідовне визначення невідомих з цієї ступеневої системи.

Прямий хід: Покладемо А11 0, якщо А11 = 0, то першим в системі запишемо рівняння, в якому А11 0.

Розставимо рівняння системи таким чином, щоб коефіцієнт при х1 мав найбільше значення (іншими словами відсортуємо систему за спаданням).

Перетворимо систему, виключивши невідоме х1 у всіх рівняннях, крім першого (використовуючи елементарні перетворення системи). Для цього помножимо обидві частини першого рівняння на і складемо почленно до другого рівняння системи. Потім помножимо обидві частини першого рівняння на і складемо з третім рівнянням системи. Продовжуючи цей процес, отримуємо систему:

Тут (I, j = ) - Нові значення коефіцієнтів і правих частин, які виходять після першого кроку.

Аналогічним чином, вважаючи головним елементом 0, виключимо невідоме х2 із усіх рівнянь системи, крім першого і другого, і т.д. Продовжуємо цей процес поки це можливо.

Якщо в процесі приведення системи (1) до ступінчастого вигляду з'являться нульові рішення (рівності виду 0 = 0) їх відкидають. Якщо ж з'явиться рівняння виду 0 = bi, а bi 0, то це говорить про несумісність системи.

Другий етап (зворотний хід) полягає у вирішенні ступеневої системи. В останньому рівнянні цієї системи висловлюємо першого невідоме xk через інші невідомі (xk +1, ..., xn). Потім підставляємо значення xk в передостаннє рівняння системи і висловлюємо xk-1 через (xk +1, ..., xn), потім знаходимо xk-2, ..., x1.