
Билет №10
1.F(x)><0 F(x)-многочлен любой степени.Методинтервалов:свойство1:Если при решении неравенства F(x)><0 многочлен F(x) может быть представлен в виде(x-x1) (x-x2)… (x-xn) где x-переменная а x1,x2,…xn – некоторые числа(корни многочлена не равные друг другу), то можно пользоваться методом интервалов. Свойство 2:в каждом из промежутков ограниченными корнями многочлена данный многочлен сохраняет свой знак, а при пережоде через корень знак меняется. 1)Представит многочлен в виде (x-x1) (x-x2)… (x-xn) где x-переменная а x1,x2,…xn – некоторые числа(корни многочлена) любым методом 2) Найти корни многочлена на числовой оси 3)Найти знаки промежутков используя предыдущее свойство 4)Записать ответ IIсвойство)Если многочлен представлен в виде (x-x1)к1 (x-x2)к2… (x-xn)кn где х- переменная ,а x1,x2,…xn –различные корни многочлена, а К1, К2… Кn- различные натуральные числа, то при переходе через корень четной степени знак не меняется, а при переходе через корень нечетной степени знак меняется на противоположный.
2. 1)ООФ - те значения аргумента при которых функция имеет смысл 2)МЗФ— множество значений, которые может принимать функция 3)Корни -те значения аргумента при которых функция равна 0 4)Промежутки знакопостоянства - это те значения аргумента при которых функция не меняет знак( Непрерывная функция – функция график которой можно начертить не отрывая руки) 5)Монотонность: Если функция или возрастает или убывает то функция монотонная. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции. 6)Четность: Функция называется четной, если выполняется два условия:
1.ООФ симметрична относительно начала отсчета 2.Для любого значения аргумента из области определения выполняется условие ∫(-х)= ∫(х)
Функция называется не четной, если выполняется два условия:
1.ООФ симметрична относительно начала отсчета
2.для любого значения аргумента из области определения выполняется условие ∫(-х)= - ∫(х) (Если не выполнено хотя бы одно условие то функция относится к функциям общего вида). 7)График - множество точек координатной плоскости, где абсцисса соответствует значению аргумента функции, а ордината соответствует значению самой функции. Способы построения: по точкам; с помощью использования параллельного переноса и симметрии.
Билет №11
1.Этапы
метода интервалов:1)Перенести слагаемые
в одну часть и разложить на множители
2)добиться равносильными преобразованиями
знака + перед старшим коэффициентом в
каждой скобке 3) отбросить скобки, которые
не меняют свой знак и не обращаются в
0. Одинаковые скобки не сокращать ,так
как можем изменить область определения
4)Отметить на оси все точки, в которых
хотя бы одна из скобок обращается в
0.Например,
![]() 5)Выколоть нули знаменателя . Например,
5)Выколоть нули знаменателя . Например,
![]() 6)Если неравенство строгое то выколоть
все нули числителя. Если неравенство
строгое, то жирно обводим все нули
числителя. Например,
6)Если неравенство строгое то выколоть
все нули числителя. Если неравенство
строгое, то жирно обводим все нули
числителя. Например,
![]() 7)Построить волну, начиная со знака +.
Помним что (x-a)2n
знака не меняет 8)Записать ответ не
забывая про изолированные решения
нестрогих неравенств.
7)Построить волну, начиная со знака +.
Помним что (x-a)2n
знака не меняет 8)Записать ответ не
забывая про изолированные решения
нестрогих неравенств.
2.
Арифметический квадратный корень из
числа a называют не отрицательное число
b квадрат которого равен a(
- радикал)
= b ↔ b≥0 b2=a
ООВ(область определения выражения
) т.к. b2=a
b2≥0
a≥0 a- подкоренное выражение Основные
тождества квадратного корня :1)
)2=a
a≥0 2)√a2
=|a| Свойства квадратного корня : I)
Квадратный корень из произведения двух
не отрицательных чисел равен произведению
корней из этих чисел. Доказательство:
Докажем по определению квадратного
корня т. е. докажем что
∙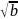 ≥0 (
∙
)2=ab
1)Докажем
∙
>0 т.к. a≥0,
b≥0
то выражения
,
имеют смысл и по определению
≥0
и
≥0 (
∙
)2=ab
1)Докажем
∙
>0 т.к. a≥0,
b≥0
то выражения
,
имеют смысл и по определению
≥0
и
 следовательно
∙
≥0 2)Докажем по свойству степени (
∙
)2=(
)2∙(
)2=ab
II)Арифметический
корень из частного , где делимое не
отрицательное число, а делитель
положительное, равен частному корня из
делимого накорень из делителя.
Доказательство:1) Докажем по определению
квадратного корня т. е. докажем что:1)
>0 2) (
следовательно
∙
≥0 2)Докажем по свойству степени (
∙
)2=(
)2∙(
)2=ab
II)Арифметический
корень из частного , где делимое не
отрицательное число, а делитель
положительное, равен частному корня из
делимого накорень из делителя.
Доказательство:1) Докажем по определению
квадратного корня т. е. докажем что:1)
>0 2) ( )2=
1)Т. к. a≥0,
b≥0
то выражения
,
имеют смысл следовательно
≥0 2) (
)2=
по свойству степени (
)2=
)2=
1)Т. к. a≥0,
b≥0
то выражения
,
имеют смысл следовательно
≥0 2) (
)2=
по свойству степени (
)2= =
Доказано! Для того чтобы освободится
от иррациональности надо и числитель
и знаменатель домножить на сопряженную
величину.
=
Доказано! Для того чтобы освободится
от иррациональности надо и числитель
и знаменатель домножить на сопряженную
величину.
Сложный радикал-
выражение вида
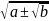 называют двойным или сложным радикалом
1)выделение полного квадрата 2)метод
неопределенных коэффициентов Билет
№12
называют двойным или сложным радикалом
1)выделение полного квадрата 2)метод
неопределенных коэффициентов Билет
№12
1
 .|F(x)|<a
F(x)<a .|F(x)|>a F(x)>a
F(x)-линейный
многочлен
a-число
.|F(x)|<a
F(x)<a .|F(x)|>a F(x)>a
F(x)-линейный
многочлен
a-число
F(x)>-a F(x)<-a
a>0 есть решения есть решения
a=0 F(x)≤a F(x)=0 F(x)=0 x- любое
a<0
нет решений x-
любое
x-
любое
|F(x)|≤ Q(x) |F(x)|≥ Q(x)
Q

 (x)≥0 Q(x)≤0
(x)≥0 Q(x)≤0
F(x)≤Q(x) Q(x)≥0
F (x)≥
-Q(x)
F(x)
≥Q(x)
(x)≥
-Q(x)
F(x)
≥Q(x)
F(x)≤-Q(x)
2.смотри билет №10 вопрос 2
Билет №13
–(не надо)
Сначала строим график у=f(х) , затем симметрично переносим часть графика оказавшегося в IIIи IVк. у. вверх. Получаем график функции у=|f(х)|.
Для того чтобы построить график функции y=∫(|x|) из графика у=∫(х) надо:
1)построить график функции у=∫(х) 2) часть графика оказавшегося в IIи III к. у. исчезает
Билет №14 ≥
Для того чтобы построить график функции y=f(x)+a надо: 1)построить функцию y=f(x) 2)сдвинуть по оси ОУ на |a| единиц если a>0 то ↑ если a<0 то ↓.
Построение графика y=f(x+l) из графика y=f(x) надо: 1)построить график y=f(x) 2)сдвигаем по оси ОХ на |l| единиц l>0 ← l<0→
Для того чтобы построить график функции y=bf(x) где b≠0 из графика y=f(x) надо:
Для того чтобы построить график функции y=f(x∙b) где b≠0 из графика y=f(x) надо:
2 .Решение
уравнений с модулем: 1.|P(x)|=a
,где а- некоторое число 1)a<0
нет корней 2) a=0
|P(x)|=a
P(x)=0
3) a>0
|P(x)|=a
P(x)=a
P(x)=-a
P(x)=-a
.Решение
уравнений с модулем: 1.|P(x)|=a
,где а- некоторое число 1)a<0
нет корней 2) a=0
|P(x)|=a
P(x)=0
3) a>0
|P(x)|=a
P(x)=a
P(x)=-a
P(x)=-a
2

 .
|P(x)|=D(x),
где P(x)
и D(x)
многочлены
|P(x)|=D(x)
↔ D(x)≥0
P(x)=D(x)
P(x)=D(x)
D(x)≥0
P(x)=-D(x)
.
|P(x)|=D(x),
где P(x)
и D(x)
многочлены
|P(x)|=D(x)
↔ D(x)≥0
P(x)=D(x)
P(x)=D(x)
D(x)≥0
P(x)=-D(x)
3 .|P(x)|=|D(x)|
↔ P(x)=D(x)
P(x)=-D(x)
.|P(x)|=|D(x)|
↔ P(x)=D(x)
P(x)=-D(x)
Билет №15
Рациональное уравнение- уравнение вида F(x) = Q(x) называется рациональным, при F(x) и Q(x) -рациональные выражения. При этом если F(x) и Q(x) - целые выражения, то уравнение называют целым; если же хотя бы одно из выражений F(x), Q(x) является дробным, то рациональное уравнение F(x) = Q(x) называется дробно рациональным.
Решение
рациональных уравнений: 1) методом
введения новой переменной Например:
![]()
![]() ]
] ![]() ↔
↔
![]()
![]()
![]()
 Ответ: -6; -2; -4
Ответ: -6; -2; -4![]()
2.Задачи, связанные с расположением корней квадратного трехчлена: 1) Найти параметр a-? если корни квадратного трехчлена принадлежат промежутку (k; m)



2)Найти значение параметра a-? При которых корни квадратного трехчлена меньше некоторого числа(k)
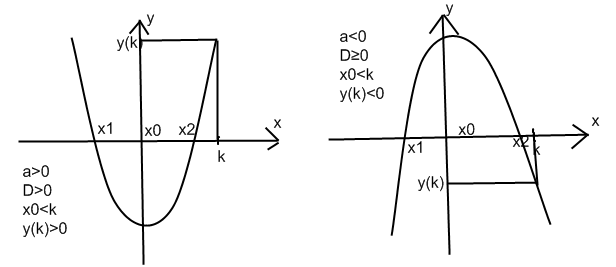


3) Найти значение параметра a-? При которых корни квадратного трехчлена больше некоторого числа(k)

Билет №16
1.смотрибилет №17 вопрос 1
2.смотри билет №14 вопрос 2
Билет №17
1. y= – обратная функция
K<0
1)ООФ - те значения аргумента при которых функция имеет смысл D(y)= (-∞;0) U (0;+∞) т. к. знаменатель не равен 0
2)МЗФ— множество значений, которые может принимать функция E(y)= (-∞;0) U (0;+∞) т. к.
k<0
3)Корни: =0 т. k≠0 то корней нет График не пересекает ос абсцис
4) Промежутки знакопостоянства- это те значения аргумента при которых функция не меняет знак( Непрерывная функция – функция график которой можно начертить не отрывая руки)
У>0 >0 х (-∞;0) т. к. k<0
У>0 на промежутке (-∞;0) график попадает в II к.у.
У<0 <0 х (0;+∞) т. к. k<0
У<0 на промежутке (0;+∞) график попадает в IV к.у.
График имеет две различные ветки т. к. с осью абсцисс не пересекается
5)Монотонность: Если функция или возрастает или убывает то функция монотонная. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
[ x1,x2 €D(y)= (-∞;0)x1 > x2
y(x1) –y(x2)= - = >0 т.к. k<0 и x1 > x2 Значит y(x1)> y(x2)
[ x1,x2 €D(y)= (0;+∞) x1 > x2
y(x1) –y(x2)= - = >0 т.к. k<0 и x1 > x2 Значит y(x1)> y(x2)
Следовательно функция монотонно возрастает
6)Четность: Функция называется четной, если выполняется два условия:
1.ООФ симметрична относительно начала отсчета
2.Для любого значения аргумента из области определения выполняется условие ∫(-х)= ∫(х)
Функция называется не четной, если выполняется два условия:
1.ООФ симметрична относительно начала отсчета
2.для любого значения аргумента из области определения выполняется условие ∫(-х)= -∫(х) (Если не выполнено хотя бы одно условие то функция относится к функциям общего вида).
1.ООФ: D(у)= (-∞;0) U (0;+∞) симметрична относительно начала отсчета
2.у(-х)= =у(х)≠- у(х) т. к. k<0 следовательно функция четная
График симметричен относительно начала отсчета
7)График-множество точек координатной плоскости, где абсцисса соответствует значению аргумента функции, а ордината соответствует значению самой функции. Значит строим только одну часть графика от (0;+∞), а вторую часть строим зеркально. Графиком этой функции является гипербола.
2.Задачи связанные с расположением корней квадратного трехчлена
Корни одного знака(+;+)или(-;-)

1)Корни положительны 2)Корни отрицательны
x


 1+x2>0
x0>0 x
1+x2Б0
x0>0
1+x2>0
x0>0 x
1+x2Б0
x0>0
x1∙x2>0 y(0)>0 x1∙x2>0 y(0)>0
D≥0 D≥0
3)Корни разных знаков
x 1∙
x2<0
y(0)<0
1∙
x2<0
y(0)<0
D≥0

4)Корни, удовлетворяющие условию x1<A<x2
