Билет №5

1. 1. Арифметический квадратный корень из числа a называют не отрицательное число b квадрат которого равен a( 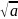- радикал) = b ↔ b≥0

b²=a

ООВ(область определения выражения ) т.к. b²=a b²≥0 a≥0 a- подкоренное выражение Основные тождества квадратного корня :1) )²=a a≥0 2)√a² =|a|

2. у=кх+b к>0

1) D(у)=(- :+ ) т.к. нет ограничений

2) E(y)=(- :+ )

3) корни kx+b=0x=- точка пересечения с осью ОХ

4) Знакопостоянство y>0 kx+b>0 kx>bт.к. k>0 знак не изменится х>-

y>0 x график в 1 углу.

y<0x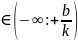 график в 3и 4 улу.

5 Монотонность

y( )-y( )=k +b-k -b=k( )>0

y( )>y( ) y(x)

6) Чётность D(y)-симметрична

Функция общего вида

7) График-прямая.

Билет №6

1. Уравнение вида ax²+bx+c=0 где х-неизвестное, а а,b,c-некоторые числа а≠0 называется квадратным уравнением(а- старший коэффициент, b-второй коэффициент, c- свободный член ) Ели в квадратном уравнении ax²+bx+c=0 хотя бы один из коэффициентов равен 0, b или c, то такое уравнение называют неполным квадратным уравнением.

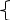1. c=0 x(ax+b)=0

a ≠0 b≠0 x=0

ax²+bx=0 ax+b=0 т.к. a≠0 то x=

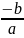
2. b 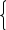=0 x²+ =0 x²-(- )=0 <0 - >0 - =-( )²

a≠0 c≠0 x²-( )²=0 a) (x- )( x+ )=0

a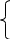 x²+c=0|:a x€(± ) b) >0 нет корней

3. a 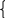≠0 x²=0 x₁=0

b=0 x₂=0

c=0

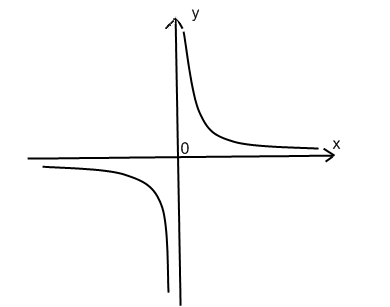
2. y= 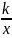– функция обратной пропорциональности где х-аргумент а к-некоторое число

k≥0

1)ООФ - те значения аргумента при которых функция имеет смысл D(y)= (-∞;0) U (0;+∞) т. к. знаменатель не равен 0

2)МЗФ— множество значений, которые может принимать функция E(y)= (-∞;+∞)

3)Корни: =0 х≠0 нет корней

4)Промежутки знакопостоянства-  это те значения аргумента при которых функция не меняет знак( Непрерывная функция – функция график которой можно начертить не отрывая руки)

У>0 >0 х (0;+∞) т. к. k≥0

У>0 на промежутке (0;+∞) график попадает в I к.у.

У<0 <0 х (-∞;0) т. к. k≥0

У<0 на промежутке (-∞;0) график попадает в III к.у.

График имеет две различные ветки т. к. с осью абсцисс непересекается

5)Монотонность: Если функция или возрастает или убывает то функция монотонная. Функция возрастает, если большему значению аргумента соответствует большее значение функции. Функция убывает, если большему значению аргумента соответствует меньшее значение функции.

[ x₁,x₂ €D(y)= (-∞;0)x₁ > x₂

y(x₁) –y(x₂)= - = 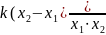<0 Значит y(x₁)< y(x₂) у(х)↓

[ x₁,x₂ €D(y)= (0;+∞) x₁ > x₂

y(x₁) –y(x₂)= - = <0 Значит y(x₁)< y(x₂) у(х)↓

Следовательно функция монотонно убывает

6)Четность: Функция называется четной, если выполняется два условия:

1.ООФ симметрична относительно начала отсчета

2.Для любого значения аргумента из области определения выполняется условие ∫(-х)= ∫(х)

Функция называется не четной, если выполняется два условия:

1.ООФ симметрична относительно начала отсчета

2.для любого значения аргумента из области определения выполняется условие ∫(-х)= -∫(х) (Если не выполнено хотя бы одно условие то функция относится к функциям общего вида).

1.ООФ: D(у)= (-∞;0) U (0;+∞) симметрична относительно начала отсчета

2.у(-х)= ≠у(х)=- у(х) т. к. k≥0 следовательно функция нечетная

График симметричен относительно начала отсчета

7)График-множество точек координатной плоскости, где абсцисса соответствует значению аргумента функции, а ордината соответствует значению самой функции. Значит строим только одну часть графика( от 0;+∞) .А вторую часть строим зеркально. Графиком этой функции является гипербола.