Курсовая работа по информатике

Сравнение методов приближенного решения уравнений

Цель: нахождение оптимального метода приближенного решения уравнения.

Задачи:

1. Изучить методы приближенного решения уравнения:

   • метод половинного деления

   • метод хорд

   • метод Ньютона

   • комбинированный метод

2. Создать компьютерные модели приближенного решения уравнений с помощью всех методов на языке программирования Pascal.

3. Провести сравнительный анализ методов.

Метод половинного деления

Алгоритм метода половинного деления основан на теореме Больцано - Коши о промежуточных значениях непрерывной функции и следствии из неё.

Теорема Больцано - Коши: если непрерывная функция принимает два значения, то она принимает любое значение между ними.

Следствие (теорема о нуле непрерывной функции): если непрерывная функция принимает на концах отрезка положительное и отрицательное значения, то существует точка, в которой она равна 0.

Алгоритм:

1. Задать отрезок [a,b] и погрешность .

2. Вычислить c=(a+b)/2

3. Определить интервал дальнейшего поиска: если f(a) и f(c) имеют разные знаки, т.е. f(a)*f(c)<0, то b:=c, в противном случае a:=c.

   f(a)*f(c)<0 (да)	f(a)*f(c)<0 (нет)

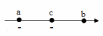
4. Если длина нового отрезка , то вычислить значение корня c=(a+b)/2 и остановиться, в противном случае перейти к шагу 2.

5. Блок-схема метода половинного деления

начало

конец

да

нет

А, В, Е

С:=(А+В)/2

(B-A)/2<=E

X:=(А-В)/2

X

нет

да

F(A)*F(C)<0

B:=C

A:=C

Метод хорд

При решении уравнения методом хорд нелинейная функция f(x) на отделенном интервале [a, b] заменяется линейной, в качестве которой берется хорда – прямая, стягивающая концы нелинейной функции. Вычисляются значения функции на концах отрезка, и строится "хорда", соединяющая точки (a, f(a)) и (b, f(b)).

При решении нелинейного уравнения методом хорд задаются интервал [a,b] на котором существует только одно решение, и точность ε. Затем через две точки с координатами (a, f(a)) и (b, f(b)) проводим отрезок прямой линии (хорду) и определяем точку пересечения этой линии с осью абсцисс, точка c. Если при этом f(a)∙f(c)<0, то правую границу интервала переносим в точку с (b=c). Если указанное условие не выполняется, то в точку c переносится левая граница интервала (а=с). Поиск решения прекращается при достижении заданной точности |f(c)|< ε.

f(a)∙f(c)<0 (да)	f(a)∙f(c)<0 (нет)

Запишем уравнение прямой, проходящей через точки с координатами (a, f(a)) и (b, f(b)):

Прямая заданная полученным уравнением пересекает ось абсцисс при условии у=0. Найдем точку пересечения хорды с осью Х.

Итак,

Далее необходимо вычислить значение функции в точке с. Если | f(c) | < 0, то полученное число и есть корень уравнения с выбранной точностью, иначе необходимо построить следующую хорду и выполнить все рассмотренные ранее действия.

Блок-схема метода хорд

начало

А, В, Е

C

конец

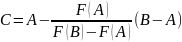
нет

да

нет

да

F(A)*F(C)>0

А:=С

В:=С

| F(C) | < E

Метод касательных

Метод касательных, иначе метод Ньютона впервые был предложен английским физиком, математиком и астрономом Исааком Ньютоном, под именем которого и обрел свою известность.

Идея, на которой основан метод касательных, аналогична той, которая реализована в методе хорд, только в качестве прямой берется касательная, проводимая в текущей точке данной функции f(x).

В одной из точек промежутка [a;b], в котором находится корень уравнения, например с, проведем касательную.

y = f(x)

Уравнение этой прямой y=kx + m.

Так как данная прямая является касательной и проходит через точку , то .

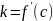Отсюда следует:

Найдем точку пересечения касательной с осью Х:

Если , то требуемая точность достигнута и x – корень уравнения; иначе, переменной с необходимо присвоить x, провести касательную через новую точку с и так продолжать до тех пор, пока .

Осталось решить, что выбрать в качестве начального приближения с.

В этой точке должны совпадать знаки функции и её второй производной. А так как нами сделано допущение, что вторая и первая производные не меняют знак, то можно проверить условие 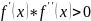на обоих концах интервала и в качестве начального приближения взять ту точку, где оно выполняется.

Блок-схема метода касательных

начало

конец

А, В, Е

C

нет

да

F (A)*F ’’(A) > 0

C:=A

C:=B

нет

| F (C) | < E

да

Комбинированный метод хорд и касательных

Если выполняются условия:

1. ,

2. сохраняют знак на отрезке .

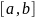то приближения корня уравнения по методу хорд и по методу касательных подходят к значению этого корня с противоположных сторон. Поэтому для быстроты нахождения корня удобно применять оба метода одновременно. Т.к. один метод даёт значение корня с недостатком, а другой – с избытком, то достаточно легко получить заданную степень точности корня.

Алгоритм решения уравнения комбинированным методом:

1. Вычислить значения функции и .

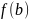2. Найти производные .

3. Для метода касательных выбирается в качестве первого приближения выбирается тот из концов отрезка , в котором выполняется условие , т.е. и одного знака.

4. Приближения корней находятся:

а) по методу касательных: ,

б) по методу хорд: .

5. Вычисляется первое приближение корня: .

6. Проверяется выполнение условия: , где - заданная точность.

Если условие не выполняется, то нужно продолжить применение метода по предыдущей схеме.

В этом случае отрезок, на котором расположен корень, сужается и имеет вид .

Вычисления продолжаются до тех пор, пока не будет найдено такое значение , при котором и совпадут с точность .