Лачх для дальнейшего удобно представить в следующем виде

,

что позволяет найти асимптотические составляющие этой характеристики:

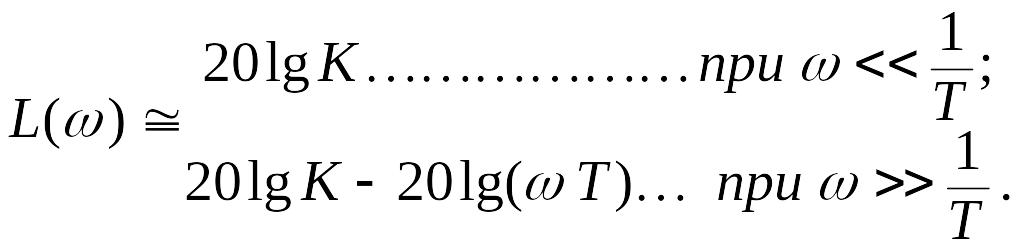
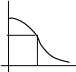
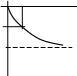
Основные виды характеристик инерционного звена приведены на рис.2.6.

Переходная и весовая характеристики, как и любая экспонента, обладают следующим важным свойством: подкасательная равна постоянной времени T. Переходная характеристика за время t=T достигает значения 0,632 , а за t=3T - значения около 0,95 , т.е. переходный процесс практически заканчивается.

Анализ АЧХ показывает, что инерционное звено по своим частотным свойствам является фильтром низкой частоты: при малых частотах ( ) отношение амплитуд выходной и входной величин близко к передаточному коэффициенту . Чем больше постоянная времени, тем меньше собственная частота (уже полоса пропускания частот).

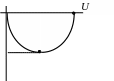
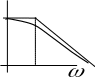
Из ФЧХ следует, что при частоте сдвиг по фазе выходного сигнала от входного равен – 45⁰, а максимально возможное отставание равно 90⁰. В практических расчетах обычно используют не фактическую, а асимптотическую ЛАЧХ. Для инерционного звена, как это следует из проведенного анализа, асимптотическая представляет собой ломаную линию в виде д вух асимптот: в области низких частот , а в области высоких частот . Обе асимптоты сопрягаются при частоте , которая называется собственной частотой апериодического звена. Наибольшая ошибка, получающаяся от приближенной замены точной ЛАЧХ двумя асимптотическими линиями, не превышает 3 при = _с.

h T A

K K А( )

0,63K h(t)

0 t

L W

20lgK

L( ) -20 W(t)

T

jV K

=0

-45

W(j )

- 90

Рис.2.6 Характеристики инерционного звена

Инерционными звеньями описываются элементы, которые способны передавать и накапливать энергию или вещество. Накопителем электрической энергии может служить конденсатор, магнитной – индуктивность, механической – упругие элементы, кинетической – движущиеся массы.

Простейшими примерами апериодического звена первого порядка являются четырехполюсники (рис.2.7.), состоящие из резистора сопротивлением r (Ом) и конденсатора емкостью C (Ф) или индуктивности L (Гн). Используя закон Ома и заменяя на получим для первого четырехполюсника (рис.2.7,а):

.

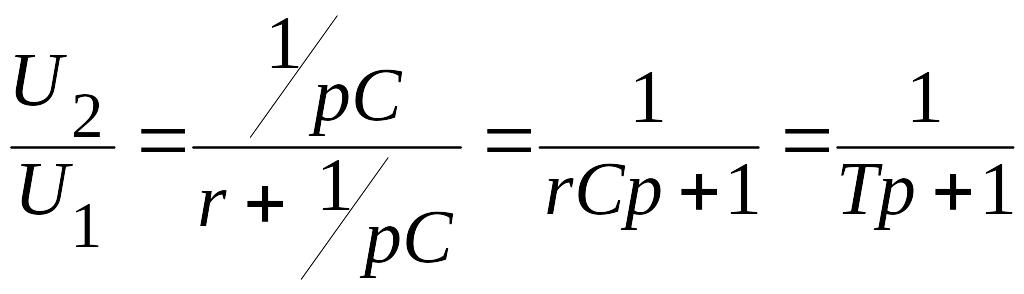Аналогично для второго четырехполюсника (рис.2.7, б)

.

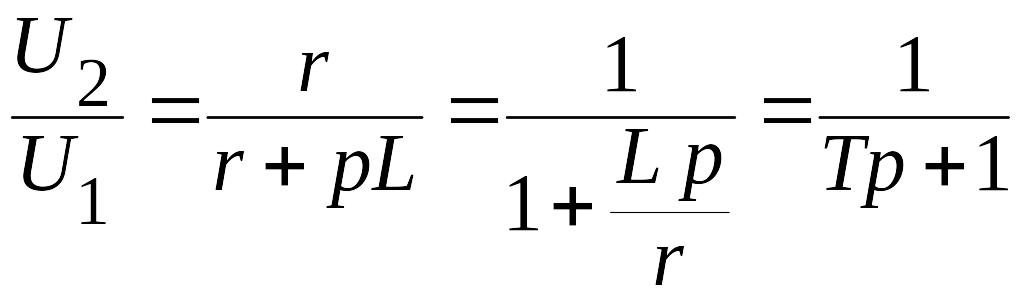Постоянные времени и измеряются в секундах.

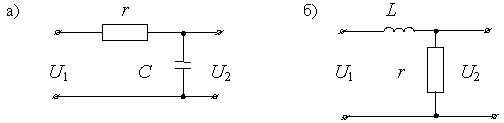
Рис.2.7 Примеры апериодического звена первого порядка

В качестве третьего примера рассмотрим сосуд, в который поступает нерегулируемый расход , а расход вытекает из сосуда через регулируемый вентиль. Расход зависит от уровня жидкости в сосуде и положения вентиля , т.е. .

Составим уравнение баланса жидкости в сосуде:

– ,

где – поверхность зеркала жидкости в сосуде.