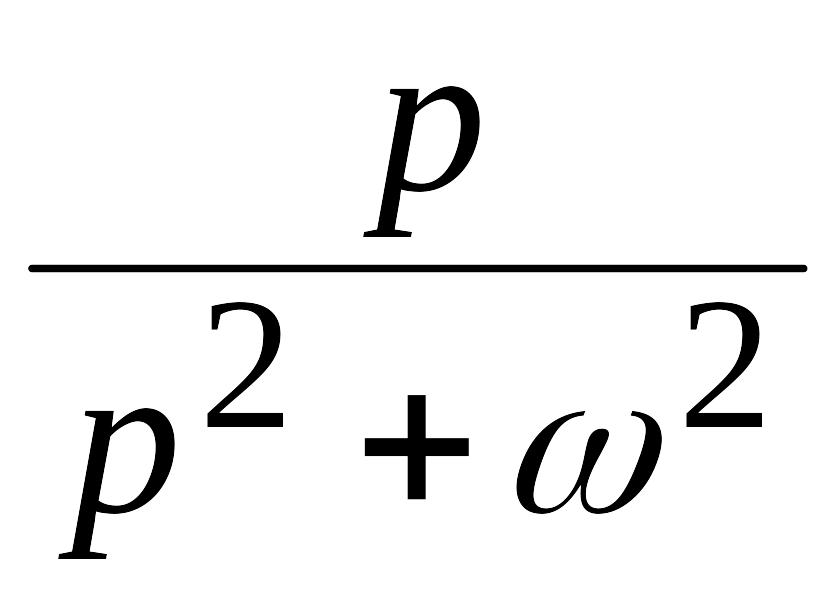- •Издательство кгту
- •Введение
- •§1.1 Принципы управления
- •§1.2 Классификация систем управления
- •Глава 2 математическое описание элементов и систем управления
- •§2.1 Назначение, особенности и методы получения моделей систем управления
- •§2.2 Операторная форма записи линейных моделей
- •§2.3 Типовые звенья и их характеристики
- •Исходя из определения передаточной функции
- •Лачх для дальнейшего удобно представить в следующем виде
- •Линеаризуем полученное уравнение
- •§2.4 Соединение звеньев и преобразование структурных схем
- •Правила преобразования структурных схем
- •Глава 3 устойчивость и качество процесса управления линейных непрерывных систем
- •§3.1 Точность систем управления при типовых воздействиях
- •§3.2 Условия и критерии устойчивости
- •Система неустойчива, если свободная составляющая неограниченно возрастает:
- •Используя (2.15) и (2.16), составим характеристическое уравнение системы
- •§3.3 Методы оценки качества переходного процесса
- •Если реальная система имеет разомкнутый контур вида
- •Для колебательных переходных процессов применяют простые
§2.2 Операторная форма записи линейных моделей
Понятие о статических и динамических характеристиках элементов и систем. Термины система, подсистема, звено можно рассматривать как синонимы, если их математические модели однотипны. В данной главе рассматриваются одноканальные объекты (звенья), в которых есть только одна выходная переменная. По характеру реакции на входное воздействие звенья могут быть разделены на статические (безынерционные) и динамические (инерционные). В статической системе выход y(t) для каждого момента времени t однозначно определяется по значениям входного воздействия U(t) в тот же момент. В динамических системах y(t) зависит не только от U(t) в тот же момент времени, но и от предыстории изменения входа в некотором интервале U[t0, t1] и совокупности величин x(t0), определяющих начальное состояние системы.
В ТАУ основное внимание уделяют динамическим САУ, в которых выделяют неустановившийся (переходной), установившийся и статический режимы работы. Переходной режим является реакцией системы (элемента) на вновь появившееся воздействие. Характер переходного процесса зависит от типа воздействия и собственных свойств системы. Установившийся (вынужденный) режим – это режим, в котором выходная величина изменяется по закону, определяемому входным воздействием. Установившийся режим имеет место после окончания переходного процесса. Статический режим – это установившийся режим при постоянном входном воздействии. Зависимость выходной величины элемента или системы от входных переменных в установившимся режиме называется статической характеристикой.
Примером
статической характеристики генератора
постоянного тока независимого возбуждения
может служить внешняя характеристика
(рис.2.1б), представляющая собой зависимость
напряжения U
на клеммах генератора от тока
![]() нагрузки при постоянных токе
нагрузки при постоянных токе
![]() возбуждения и скорости вращения
возбуждения и скорости вращения
![]() якоря. Режим, на который, как правило,
рассчитана работа генератора или другого
технического устройства, будем называть
базовым или номинальным (обозначен
индексом О). В общем случае статические
характеристики являются нелинейными.
якоря. Режим, на который, как правило,
рассчитана работа генератора или другого
технического устройства, будем называть
базовым или номинальным (обозначен
индексом О). В общем случае статические
характеристики являются нелинейными.

Рис.2.1 Принципиальная схема генератора постоянного тока (а)
и его внешняя характеристика (б)
Линеаризация. Переходные (неустановившиеся) режимы в большинстве случаев описываются нелинейными дифференциальными уравнениями. Обычно стремятся заменить исходные нелинейные уравнения линейными, приближенно описывающими процессы в системе (элементе). Процесс преобразования нелинейных уравнений в линейные называют линеаризацией. Переход к линейным уравнениям существенно упрощает моделирование, анализ и синтез САУ.
В нормально функционирующей САУ фактический режим обычно незначительно отличается от номинального режима. Это позволяет произвести линеаризацию, раскладывая нелинейные функции в ряд Тейлора и ограничиваясь линейными членами, если линеаризуемая функция обладает непрерывными частными производными по всем аргументам в окрестности базового режима.
Геометрически
линеаризация означает (рис.2.2) замену
исходной кривой АВ отрезком ее касательной
![]() в точке 0, соответствующей базовому
режиму.
в точке 0, соответствующей базовому
режиму.

Рис.2.2 Линеаризация кривой АВ
Линеаризованное уравнение удобно записывать в отклонениях от базового режима, что равносильно переносу начала координат в точку 0. Уравнение касательной в отклонениях имеет вид:
![]() ,
,
где
![]() –
коэффициент передачи;
–
коэффициент передачи;
![]() ,
,
![]() .
.
Значение
![]() является мерой статизма элемента или
системы. Если
является мерой статизма элемента или
системы. Если
![]() =0
(выходная координата не зависит от
входной), то элемент (система) является
астатическим относительно рассматриваемой
входной координаты.
=0
(выходная координата не зависит от
входной), то элемент (система) является
астатическим относительно рассматриваемой
входной координаты.
Рассмотренный прием можно применить и для линеаризации дифференциального уравнения. Для примера рассмотрим уравнение второго порядка
![]() ,
,
где
![]() и
и
![]() – первые производные по времени;
– первые производные по времени;
![]() – вторая
производная по времени.
– вторая
производная по времени.
Линеаризуя это уравнение, получим:
 .
.
Таким образом, линеаризация функции (уравнения) сводится к составлению суммы произведений частных производных линеаризуемой функции (уравнения) по каждому аргументу, вычисленных в точке, соответствующей базовому режиму функционирования объекта (системы), на отклонение аргумента, по которому выполнялось дифференцирование.
Система (элемент), процессы в которой описываются линейными (линеаризованными) уравнениями, является линейной.
Линейные операторы обладают свойствами однородности и аддитивности. Это означает, что в линейной системе выходная переменная изменяется пропорционально усилению (ослаблению) входного воздействия, а реакция на сумму любых воздействий равна сумме реакций на эти воздействия. Иными словами реакция линейной системы на линейную комбинацию воздействий равна той же линейной комбинации реакций системы на каждое воздействие в отдельности. Это свойство, называемое принципом суперпозиции, в частности, позволяет исследовать СУ относительно каждого внешнего воздействия без учета остальных воздействий, что существенно упрощает решение задач анализа и синтеза.
Рассмотренная методика линеаризации применима для функций, которые можно разложить в ряд Тейлора, т.е. когда функция является аналитической в рабочей области.
Форма
записи дифференциальных уравнений.
Математические
модели элементов и системы в целом в
ТАУ часто представляют обыкновенными
дифференциальными уравнениями записанными
в операторной (символической) форме,
основанное на использовании условного
(символического) обозначения производных
и интеграла:  ,
где
,
где
![]() =1,2,3…;
=1,2,3…;
![]() .
.
При
записи дифференциальных уравнений в
операторной форме оператор
![]() следует
рассматривать как алгебраический
сомножитель, а выражение
следует
рассматривать как алгебраический
сомножитель, а выражение
![]() – как
произведение, не обладающее свойством
коммутативности: нельзя вместо рy
писать
– как
произведение, не обладающее свойством
коммутативности: нельзя вместо рy
писать
![]() .
.
Дифференциальные уравнения в ТАУ обычно приводят к стандартной форме, для чего делят все члены уравнения на коэффициент слагаемого при выходной координате, не содержащего оператор . Если коэффициент равен нулю, деление выполняют на первый, отличный от нуля, коэффициент при самой младшей производной от выходной координаты.
При записи линейных уравнений в ТАУ принято выходную величину и ее производные записывать в левой части уравнения, а все остальные члены переносить в правую часть. Все перечисленные правила делают запись дифференциальных уравнений более компактной и удобной для практического применения.
Пусть объект описывается следующим уравнением
![]() .
.
Вводя
оператор (символ) дифференцирования
![]() ,
получим:
,
получим:
![]() ,
,
или в более компактной форме
![]() .
.
Запишем последнее уравнение в стандартной форме:
![]() .
.
Широко
пользуются следующими обозначениями:
![]()
![]()
![]() .
.
Коэффициенты
![]() и
и
![]() имеют размерность времени и называются
постоянными времени. Коэффициент
передачи
характеризует передаточное отношение
элемента (системы) в установившемся
режиме. Размерность
определяется размерностями переменных
имеют размерность времени и называются
постоянными времени. Коэффициент
передачи
характеризует передаточное отношение
элемента (системы) в установившемся
режиме. Размерность
определяется размерностями переменных
![]() и
и
![]() .
.
С учетом принятых обозначений исходное дифференциальное уравнение приводим к стандартной форме:
![]()
Решить
уравнение, т.е. найти реакцию элемента
![]() на изменение
на изменение
![]() ,
можно, если задан закон изменения
и определены начальные условия
,
можно, если задан закон изменения
и определены начальные условия
![]() ;
;
![]() ;
;
![]() .
.
В ТАУ широко пользуются нулевыми начальными условиями, полагая:
![]()
![]()
![]() .
.
В
более общем случае модель вида «вход–выход»
описывается скалярным обыкновенным
линейным дифференциальным уравнением
![]() –порядка
с постоянными коэффициентами, которые,
используя операторные полиномы
–порядка
с постоянными коэффициентами, которые,
используя операторные полиномы
![]() и
и
![]() или А(р) и В(р), можно записать в компактной
форме
или А(р) и В(р), можно записать в компактной
форме
![]() ,
(2.1)
,
(2.1)
где
![]() – собственный оператор;
– собственный оператор;
![]() – оператор
воздействия.
– оператор
воздействия.
Понятие о передаточной функции. Уравнение (2.1) часто представляют в следующем виде
![]() .
(2.2)
.
(2.2)
Отношение оператора воздействия к собственному оператору звена называют операторной передаточной функцией W(p), которую записывают не производя возможных сокращений. Запись (2.2) является чисто символической и не дает решения уравнения (2.1).
Для рассматриваемого примера:
![]() .
.
Передаточная
функция не зависит от закона изменения
внешнего воздействия и определяется
только свойствами элемента относительно
выбранного воздействия. При одной
выходной координате число
![]() ,
характеризующих динамику элемента,
определяется числом входных переменных.
,
характеризующих динамику элемента,
определяется числом входных переменных.
Более
строгое определение передаточной
функции как наиболее компактной формы
описания динамических свойств элементов
и систем основано на применении
преобразования Лапласа. При этом
считается, что рассматриваемой функции
времени
,
которую называют оригиналом, можно
найти «лапласово изображение»
![]() :
:
![]() ,
,
где – комплексная переменная.
Преобразование
Лапласа возможно, если:
![]() при
при
![]() ;
при
;
при
![]() растет не быстрее некоторой показательной
функции
растет не быстрее некоторой показательной
функции
![]() ,
где
,
где
![]() и
и
![]()
![]() постоянные;
на любом конечном отрезке времени
однозначна, конечна и кусочно–непрерывна.
постоянные;
на любом конечном отрезке времени
однозначна, конечна и кусочно–непрерывна.
Составлены таблицы (примеры даны в табл.2.1), позволяющие определять изображение по оригиналу и выполнять обратное преобразование Лапласа, т.е. находить оригинал по изображению.
В основе этого способа перехода от дифференциальных уравнений к передаточным функциям лежат следующие правила:
![]() ;
;
![]() ,
,
справедливые
при нулевых начальных условиях. Здесь
![]() – символ интеграла Лапласа (читается
Лапласиан). Обратное преобразование
Лапласа, позволяющее найти оригинал по
изображению, обозначают
– символ интеграла Лапласа (читается
Лапласиан). Обратное преобразование
Лапласа, позволяющее найти оригинал по
изображению, обозначают
![]() .
.
Применим приведенные правила к дифференциальному уравнению второго порядка
 ,
,
получим алгебраическое уравнение
![]() ,
,
где – комплексная переменная.
Отношение изображения по Лапласу выходной величины к изображению входной величины при нулевых начальных условиях называют передаточной функцией
 .
.
Совпадение по форме выражений для передаточных функций, полученных с использованием операционного исчисления (преобразования Лапласа) и символической (операторной) записи дифференциального уравнения, позволяет определять по дифференциальному уравнению без преобразования его по Лапласу. Следует подчеркнуть, что сходство между этими чисто внешнее и имеет место лишь для стационарных систем, т.е. для случая, когда коэффициенты уравнения постоянны.
Таблица 2.1
Изображение простейших функций времени по Лапласу
Наименование функции |
X(t) |
X(p) |
Дельта-функция |
|
1 |
Ступенчатая функция |
|
|
Степенная функция |
|
|
Экспонента |
|
|
Синусоида |
|
|
Косинусоида |
|
|
Таким образом, передаточную функцию формально можно получить из линейного дифференциального уравнения при нулевых начальных условиях, путем замены в нем символа дифференцирования оператором и деления образующегося при этом коэффициента или многочлена правой части (оператора воздействия) уравнения на многочлен левой части (собственный оператор). При таком переходе следует избегать сокращения общих делителей полиномов числителей и знаменателей (диполей рациональных функций). Такое сокращение приводит к потере составляющих свободных движений, вызванных ненулевыми предначальными условиями.
Оператор W(p), связывающий вход звена с выходом, характеризуется структурой и параметрами. Параметрами оператора являются коэффициенты полиномов А(р) и В(р), а структура определяется заданием степеней n и m (2.1), где n – определяет порядок дифференциального уравнения.
Наряду с полиноминальной формой (2.2) передаточная функция может быть задана в факторизованном виде
 ,
(2.3)
,
(2.3)
где
![]() – множество нулей, т.е. корней уравнения
В(р)=0;
– множество нулей, т.е. корней уравнения
В(р)=0;
![]() – множество
полюсов, т.е. корней уравнения А(р)=0.
– множество
полюсов, т.е. корней уравнения А(р)=0.
Передаточные функции, все нули и полюсы которых находятся в левой полуплоскости, называют минимально-фазовыми.
Понятие о временных и частотных характеристиках звеньев и систем. Наглядное представление о свойствах элемента (системы) дает решение дифференциального уравнения, описывающего его динамику при типовых (регулярных) внешних воздействиях и нулевых начальных условиях.
В
качестве типовых воздействий обычно
используют единичную ступенчатую
функцию (функцию Хевисайда)
![]() ;
единичную импульсную функцию
(дельта-функцию)
;
единичную импульсную функцию
(дельта-функцию)
![]() ;
гармоническую функцию
;
гармоническую функцию
![]() .
.
Аналитическое
представление единичной ступенчатой
функции имеет вид
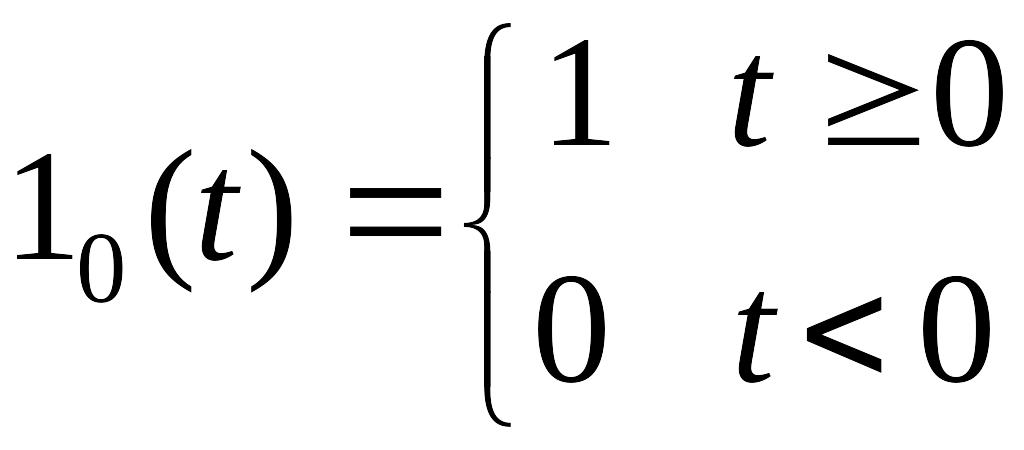 .
.
Реакцию
элемента (системы) при подаче на его
вход единичного ступенчатого воздействия
и нулевых начальных условиях называют
переходной функцией и обозначают
![]() .
График зависимости
от времени
.
График зависимости
от времени
![]() называется переходной характеристикой
(рис.2.3).
называется переходной характеристикой
(рис.2.3).

Рис.2.3 Графики и
Дельта-функция аналитически определяется следующим образом:
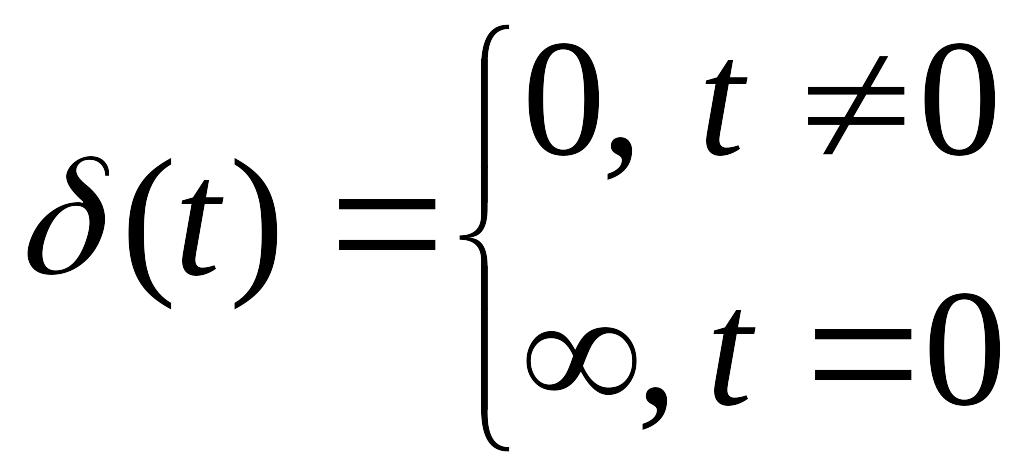 ;
;
![]() .
.
Реакцию
элемента (системы) при подаче на его
вход сигнала в форме дельта–функции и
нулевых начальных условиях называют
импульсной переходной функцией (функцией
веса); обозначают эту функцию
![]() .
График
называют импульсной переходной
характеристикой. Рис.2.4а поясняет
определение
,
а на рис.2.4б приведены график, упрощенно
трактующий понятие дельта–функции, и
пример характеристики
.
.
График
называют импульсной переходной
характеристикой. Рис.2.4а поясняет
определение
,
а на рис.2.4б приведены график, упрощенно
трактующий понятие дельта–функции, и
пример характеристики
.
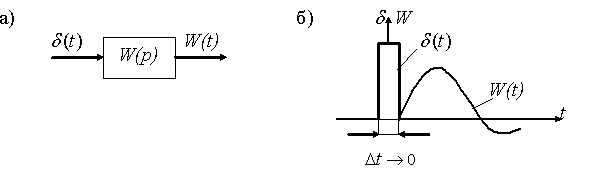
Рис.2.4 Наглядное
представление определения
![]() (рис.а)
(рис.а)
и графики и (рис.б)
Дельта–функция обладает следующими важными свойствами.
![]() ;
;
![]() ;
;
![]() .
.
Передаточная, переходная и весовая функции связаны между собой следующими соотношениями:
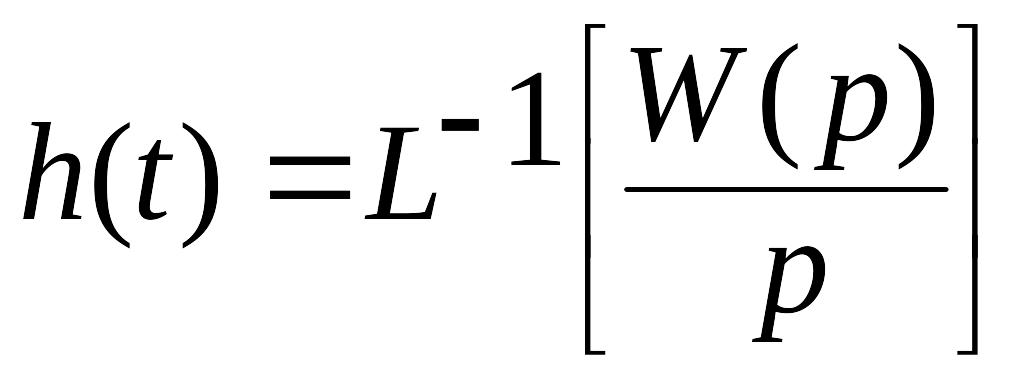 ;
;
![]() ;
;
![]() .
.
Если
известна функция веса W(t),
то реакция элемента (системы) y(t)
на переменную x(t)
определяется интегралом свертки
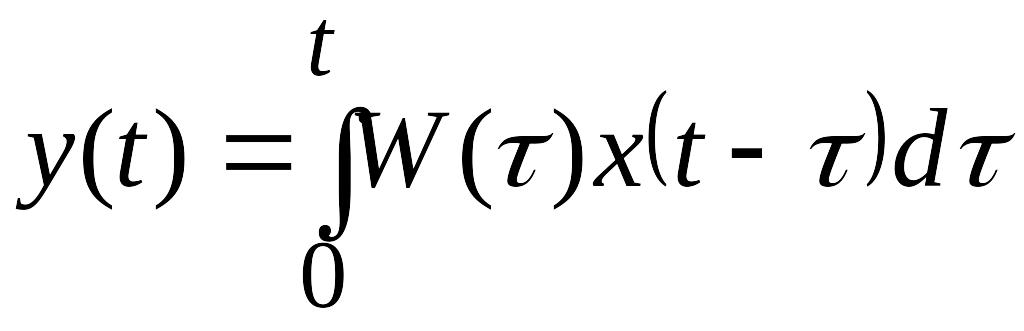 ,
т.е. оператор преобразования имеет форму
интегрального уравнения.
,
т.е. оператор преобразования имеет форму
интегрального уравнения.
Частотные характеристики, определяющие взаимосвязь между параметрами установившихся периодических входных и выходных сигналов, является важной формой представления динамических характеристик объектов и систем управления. С математической точки зрения гармоническое воздействие может рассматриваться как сумма двух экспоненциальных воздействий

Использование экспоненциальных функций удобно, так как производная и интеграл от таких функций представляет собой экспоненциальные функции.
К линейным системам применим принцип суперпозиции, поэтому при решении конкретных задач ищется эффект, создаваемый каждым из экспоненциальных воздействий в отдельности.
Вынужденные колебания, вызываемые в линейной динамической системе гармоническим воздействием, представляют собой также гармоническую функцию времени, имеющую ту же угловую частоту ω, что и воздействие, но отличающееся от последнего по амплитуде и по фазе.
Частотная
передаточная функция
![]() ,
которую часто называют комплексным
коэффициентом передачи, получается
заменой
на
,
которую часто называют комплексным
коэффициентом передачи, получается
заменой
на
![]() в передаточной
функции
,
т.е.
в передаточной
функции
,
т.е.
![]()

![]()
Функцию можно представить в виде
![]() ,
,
где
![]() ;
;
![]() ;
;
![]() ,
,
![]() ,
,
![]() и
и
![]() (
(![]() )
– соответственно вещественная, мнимая,
амплитудная и фазовая частотные функции.
Графики зависимости
)
– соответственно вещественная, мнимая,
амплитудная и фазовая частотные функции.
Графики зависимости
![]() ,
,
![]() ,
,
![]() и
и
![]() называют амплитудной, фазовой, вещественной
и мнимой частотными характеристиками,
а годограф вектора
при изменении частоты от 0 до
называют амплитудной, фазовой, вещественной
и мнимой частотными характеристиками,
а годограф вектора
при изменении частоты от 0 до
![]() (или от –
до
)
– амплитудно-фазовой характеристикой
(АФХ).
(или от –
до
)
– амплитудно-фазовой характеристикой
(АФХ).
Минимально–фазовым передаточным функциям соответствуют меньшие по модулю фазовые сдвиги в сравнении с другими W(p), имеющими ту же АЧХ, но часть нулей и/или полюсов которых расположена справа от мнимой оси. Для минимально-фазовых систем характерно наличие однозначной связи A(ω) с φ(ω), что существенно упрощает анализ и синтез таких систем.
Функцию
![]() называют логарифмической амплитудной
частотной функцией, а график зависимости
называют логарифмической амплитудной
частотной функцией, а график зависимости
![]() от логарифма частоты
от логарифма частоты
![]() – логарифмической амплитудной частотной
характеристикой (ЛАЧХ). При построении
ЛАЧХ по оси абсцисс откладывают частоту
в логарифмическом масштабе, но на
отметках, соответствующих
– логарифмической амплитудной частотной
характеристикой (ЛАЧХ). При построении
ЛАЧХ по оси абсцисс откладывают частоту
в логарифмическом масштабе, но на
отметках, соответствующих
![]() ,
пишут значение
,
а не
.
Единицей
является децибел. Интервал, на котором
изменяется частота в 10 раз, называется
декадой.
,
пишут значение
,
а не
.
Единицей
является децибел. Интервал, на котором
изменяется частота в 10 раз, называется
декадой.
Логарифмической фазовой частотной характеристикой (ЛФЧХ) называют график зависимости фазовой частотной функции ( ) от логарифма частоты .
Расчет временных характеристик. В ТАУ для решения дифференциальных уравнений широко используют операционный метод, позволяющий учесть и ненулевые начальные условия.
Для обыкновенных дифференциальных уравнений (2.1) и типовых воздействий y(p) является дробно-рациональной функцией.
 ,
(2.4)
,
(2.4)
причем m<n и коэффициенты аi и bi действительные. Если известны полюсы, то указанную зависимость можно переписать в виде
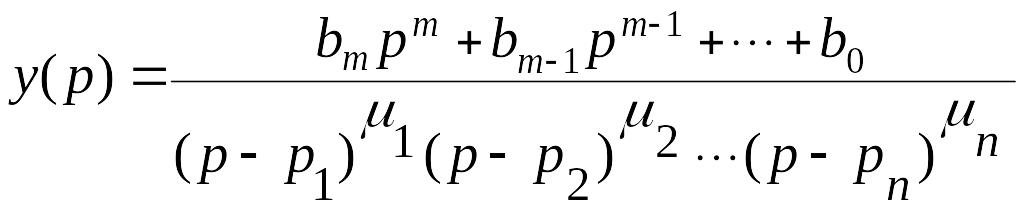 ,
(2.5)
,
(2.5)
где
![]() – кратность корня pi.
– кратность корня pi.
При различных вещественных или комплексных корнях оригинал определяется формулой
![]() ,
(2.6)
,
(2.6)
где
 ;
;
![]() – производная
– производная
![]() по р.
по р.
Если один из корней изображения равен нулю, т.е.
![]() ,то
,то
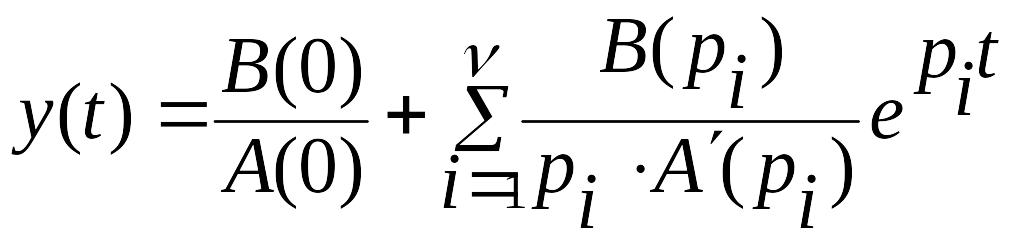 .
(2.7)
.
(2.7)
В практических расчетах при вычислении временных характеристик находит применение метод неопределенных коэффициентов, в соответствии с которым y(p) представляют в виде суммы простых дробей с последующим определением оригинала для каждого слагаемого.
Поясним этот метод на примере
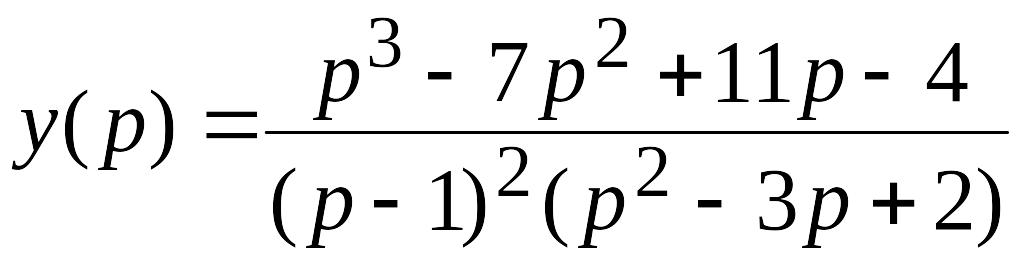 .
.
Разложив y(p) на сумму простых дробей

и приведя к общему знаменателю, получим
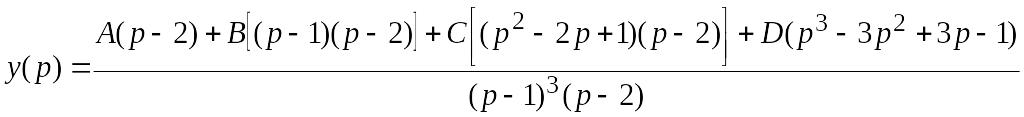 .
.
Приравнивая коэффициенты числителей при одинаковых степенях р, имеем систему уравнений, решая которую находим А= –1, В= –1, С=3, D= –2.
Поскольку
 ;
;
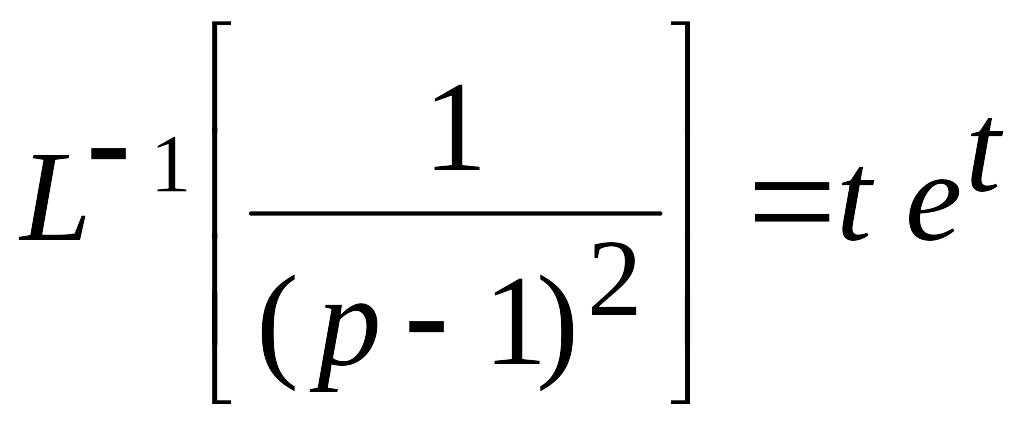 ;
;
 ,
получим искомую зависимость
,
получим искомую зависимость
![]() .
.
Упростить вычисление переходной функции h(t) по изображению y(p) вида (2.4) при
![]()
можно, если вначале определить переходную функцию h0(t) при В(р)=1. Затем вычисляется переходная функция h(t), соответствующая заданному оператору В(р) по формуле
![]() .
.
В общем случае система, описываемая уравнением (2.1), в момент подачи входного сигнала х(t) может иметь ненулевые начальные условия
![]() .
.
Учитывая следующее свойство изображений
 ,
,
преобразуем уравнение (2.1) по Лапласу:

Используя ранее принятые (2.1) обозначения А(р) и В(р), запишем зависимость, определяющую изображение выходного сигнала[1]
![]() ,
(2.8)
,
(2.8)
где
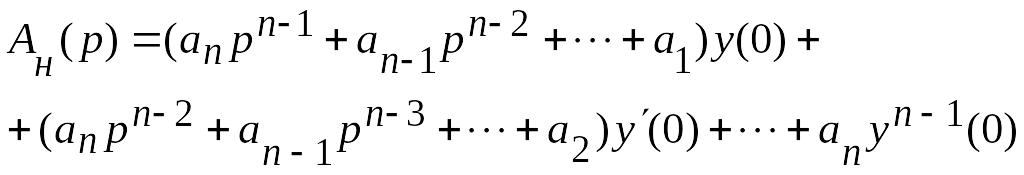
полином,
определяемый ненулевым состоянием
системы в момент, предшествующий
воздействию х(t),
т.е. предначальными условиями. Ненулевое
предначальное состояние может быть
порождено воздействием, поступившим
на систему на промежутке
![]() .
.
Если
х(р) представить в виде
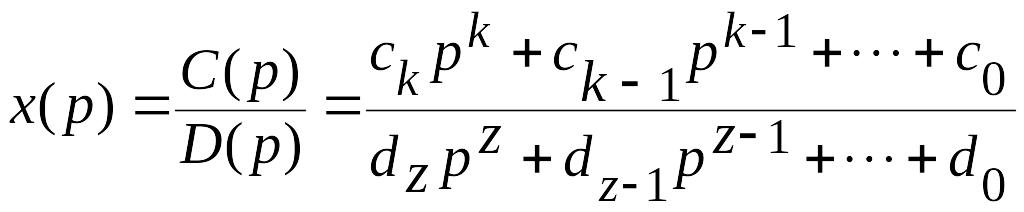 ,
(2.9)
,
(2.9)
то
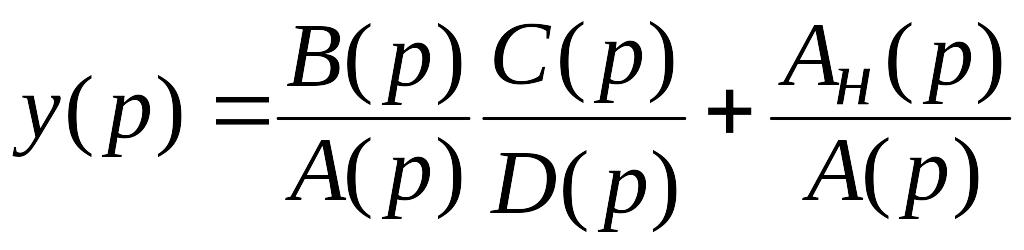 .
(2.10)
.
(2.10)
Выходной сигнал, соответствующий изображению y(p), равен
![]() ,
(2.11)
,
(2.11)
где
 ;
;
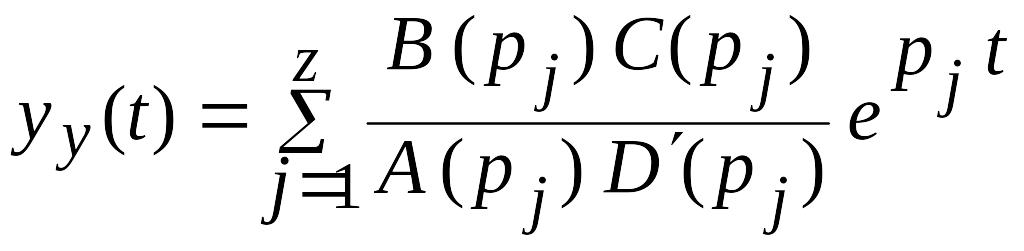 ;
;
 ,
,
![]() – полюсы
передаточной функции В(р)/A(p);
– полюсы
передаточной функции В(р)/A(p);
![]() –
полюсы
изображения воздействия С(р)/D(p);
–
полюсы
изображения воздействия С(р)/D(p);
![]() ,
т.е. полюсы воздействия не равны полюсам
передаточной функции.
,
т.е. полюсы воздействия не равны полюсам
передаточной функции.
Установившееся
вынужденное движение
![]() при обработке воздействия х(t) порождается
его полюсами.
при обработке воздействия х(t) порождается
его полюсами.
Переходная
составляющая вынужденного движения
![]() ,
характеризующая динамические (инерционные)
свойства системы, образуется из-за
изменения начальных условий внешним
воздействием в начальный момент времени
(t=0).
,
характеризующая динамические (инерционные)
свойства системы, образуется из-за
изменения начальных условий внешним
воздействием в начальный момент времени
(t=0).
Свободное
движение
![]() вызвано ненулевыми предначальными
условиями. Закономерности изменений
и
определяются полюсами передаточной
функции.
вызвано ненулевыми предначальными
условиями. Закономерности изменений
и
определяются полюсами передаточной
функции.
Если
полиномы А(р) и В(р) не являются взаимно
простыми, т.е. имеют диполи – нетривиальные
общие делители
![]() ,
то система называется неполной, а
передаточная функция вырожденной.
Реакция такой системы на типовые
воздействия, т.е. временные характеристики
h(t)
и W(t),
не отражают полностью собственные
свойства системы. Сокращать диполи
вырожденной W(р)
не рекомендуется, а в случае правого
полюса – недопустимо. Поэтому анализу
систем должно предшествовать определение
возможности наличия общих делителей в
операторных полиномах передаточной
функции.
,
то система называется неполной, а
передаточная функция вырожденной.
Реакция такой системы на типовые
воздействия, т.е. временные характеристики
h(t)
и W(t),
не отражают полностью собственные
свойства системы. Сокращать диполи
вырожденной W(р)
не рекомендуется, а в случае правого
полюса – недопустимо. Поэтому анализу
систем должно предшествовать определение
возможности наличия общих делителей в
операторных полиномах передаточной
функции.
Если
предначальные условия, вызванные
воздействием, приложенным к любому из
входов, таковы, что
![]() ,
то
содержит составляющую (моду), соответствующую
полюсу
,
то
содержит составляющую (моду), соответствующую
полюсу
![]() .
.
Анализ зависимости (2.11) позволяет найти и условия удовлетворительного воспроизведения входного воздействия.
Заключение. Динамические свойства одномерных (одноканальных) линейных звеньев и систем могут быть представлены дифференциальными уравнениями, передаточными, переходными, весовыми и частотными функциями. Перечисленные преобразования входных переменных в выходные являются основными формами представления конечномерных линейных стационарных детерминированных операторов. Следует подчеркнуть, что частотные характеристики определяются в установившемся (вынужденном) режиме работы элемента (системы), но характеризуют и динамические свойства исследуемого объекта.
Амплитудно–частотная характеристика имеет размерность, равную отношению размерности выходной величины к размерности входной, и определяет зависимость коэффициента передачи звена от частоты. Фазо–частотная характеристика показывает, какое отставание или опережение выходного сигнала по фазе создает звено при различных частотах. Реальные технологические объекты с повышением частоты хуже пропускают сигналы, т.е. ослабляют амплитуду и вносят отрицательный фазовый сдвиг.
Амплитудно-частотные характеристики в логарифмических координатах можно аппроксимировать отрезками прямых линий и строить без громоздких вычислений. ЛАЧХ – удобная для практических расчетов форма представления частотных характеристик.
Все перечисленные функции (характеристики) однозначно связаны с уравнением звена (системы). Временные и частотные характеристики могут быть сняты экспериментально или построены по уравнению звена. Переходу от экспериментально полученных временных или частотных характеристик к передаточной функции обычно предшествует выбор структуры оператора. Результаты такого перехода неоднозначны, т.к. зависят от выбора структуры W(p) оператора и алгоритма обработки данных. Реакция неполной системы, т.е. системы с вырожденной передаточной функцией, на типовые воздействия не отражает полностью собственные свойства системы.