Дополнительная

1. Борытко, Н.М. Методология и методы психолого-педагогических исследований: учеб. пособие / Н.М. Борытко, А.В. Моложавенко, И.А. Соловцова; под ред. Н.М. Борытко. – 2-е изд., стер. – М.: Академия, 2009. – 320 с.

2. Загвязинский, В.И. Как учителю подготовить и провести эксперимент: метод. пособие / В.И. Загвязинский, М.М. Поташник. – М.: Педагогическое общество России, 2006. – 142 с.

3. Маслак, А.А. Основы планирования и анализа сравнительного эксперимента в педагогике и психологии / А.А. Маслак. – Курск: РОССИ, 1998. – 167 с.

4. Методы системного педагогического исследования: учеб. пособие / Н.В. Кузьмина, Е.А. Григорьева, В.А. Якунин и др. – М.: Нар. образование, 2002. – 208 с.

5. Сидоренко, Е.В. Методы математической обработки в психологии / Е.В. Сидоренко. – СПб.: Речь, 2001. – 349 с.

6. Фомичева И.Г. Модели педагогической деятельности: опыт систематизации / И.Г. Фомичева. – Тюмень: Изд-во Тюмен. гос. ун-та, 1997. – 254 с.

Приложение 2

Задания для самостоятельной работы слушателям специальности «Информатика» по дисциплине «Технологии программирования и методы алгоритмизации»

1. В конце XIX века в Европе появилась игра под названием «Ханойские башни». Реквизит игры состоит из 3 игл, на которых размещается башня из колец.

Цель игры – перенести башню с левой иглы (1) на правую (3).

Правила игры: за один раз можно переносить только одно кольцо; запрещается помещать большее кольцо над меньшим.

Составить алгоритм решения данной задачи (количества колец – N<10).

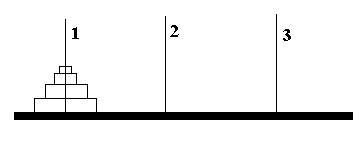
2. Составить алгоритм подсчета количества способов, которыми можно разменять рубль монетами достоинством 1; 2; 3; 5 копеек.

3. Экран компьютера представляет точечный растр, произвольная прямая линия на экране состоит из некоторого множества горизонтальных отрезков – штрихов. Составьте алгоритм (программу) для построения на экране произвольного отрезка прямой с координатами: X0, Y0 – координаты первой точки отрезка; X1, Y1 – координаты последней точки отрезка. Внимание: ваш компьютер имеет команды только для построения точек или горизонтальных и вертикальных штрихов.

4. Написать программу расшифровки сообщения, закодированного по описанному ниже принципу. Пусть дан шифр (набор цифр 432513) и текст – « настоящий виновник кражи алмазов». Записываем текст без пробелов и под ним цифры шифра:

настоящийвиновниккражиалмазов

43251343251343251343251343251

сгучпвэллжйртепнлнфгинборгйуг

Каждая буква алфавита заменяется на букву, номер которой равен номеру исходной буквы в алфавите плюс цифра, стоящая под ней. При этом буква с номером 33+К есть буква с номером К.

5. Новобранцы выстроились в ряд, и старшина скомандовал: «Направо!», после чего каждый повернулся в произвольном направлении на 90 градусов, но, увидев лицо соседа, тут же повернулся на 180 градусов. Перестанут ли они когда-нибудь вертеться? Результат обосновать. Составить программу, иллюстрирующую эту ситуацию.

6. Черепашка находится в городе, все кварталы которого имеют прямоугольную форму и ей необходимо попасть с крайнего северо-западного перекрестка на крайний юго-восточный. Пример:

Н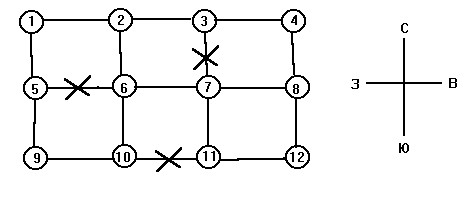 а некоторых улицах проводится ремонт и по ним запрещено движение (например, между 3 и 7 перекрестками, 5 и 6, 10 и 11), длина, а значит и стоимость проезда, по остальным улицам задается. Кроме того, для каждого перекрестка определена стоимость поворота. Так, если Черепашка пришла на 7-й перекресток и поворачивает к 11-му, то она платит штраф, а если идет в направлении 8-го, то платить ей не приходится. Найти для Черепашки маршрут минимальной стоимости.

Исходные данные:

N – количество перекрестков, определяется через два числа k,m и N=k*m (1<k,m<11);

Длина улиц (стоимость проезда) и стоимость поворота на перекрестках – целые числа.

7. В организации N рабочих (2<N<31). Каждый из них оказывает влияние на некоторое количество других рабочих (не обязательно всех). Влияние оценивается некоторым положительным числом. Так, если рабочий с номером i влияет на рабочего с номером j, то степень влияния это число C[i,j]. Итак, совокупность влияний можно описать матрицей N*N. Нулевой элемент матрицы – нет влияния.

Руководитель организации решил упорядочить влияния, считая, что тем самым он повысит производительность труда. Для исследования того, как это сделать, он пригласил социолога.

Первое предложение социолога заключалось в том, чтобы выделить совокупность связей (влияний) максимального веса, при этом на каждого рабочего должен влиять только один человек, все рабочие должны быть охвачены связями, а остальные связи (влияния) запрещаются в директивном порядке на время работы. Пример работы социолога.

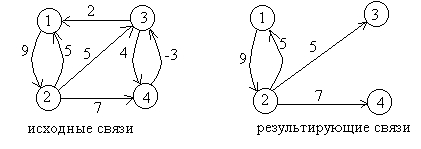
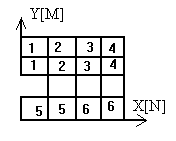
Второе предложение социолога заключалось в поиске лидера и организации связей так, как это показано на следующем рисунке (если это можно сделать). На лидера не влияет никто. На каждого рабочего может влиять только один человек, в то время как он может влиять на любое количество рабочих. Если рабочий с номером i оказывает влияние на рабочего с номером j, то ни один рабочий с номером j и ни один из его «СЫНОВЕЙ» не может оказывать влияния на рабочего с номером i и на всех его «ПРЕДКОВ». При этом следует выбирать вариант с максимальным суммарным весом связей.

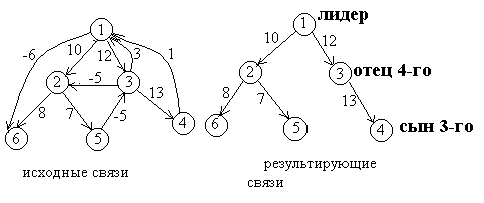
Разработать программу, которая должна обеспечивать помощь социологу в том и другом случаях.

8. Автостоянка имеет форму клеточного поля N*M. Одна клетка на границе является выездом с автостоянки. Любой автомобиль занимает две соседние клетки (по горизонтали или по вертикали, но не по диагонали!).

Написать программу поиска размещения максимального количества автомобилей, такого, что любой из автомобилей имеет возможность выезда.

Автомобиль может выехать, если у его «границ» есть хотя бы одна свободная клетка и, перемещаясь по свободным клеткам, он может «добраться» до выезда.

Входные данные. Натуральные числа N и M(N, M100) и координаты клетки выезда.

Выходные данные. Число размещенных автомобилей.

Пример.

N, M  4, 4

клетка выезда  1, 2

Количество автомобилей  6

9. Часы древних марсиан устроены следующим образом: из большой корзины каждую секунду выкатывается шарик и попадает в первую корзину. Как только в ней накапливается пять шариков, корзина переворачивается и четыре шарика возвращаются в большую корзину, а пятый шарик попадает во вторую корзину. Как только во второй корзине накапливается шесть шариков, пять из них возвращаются в большую корзину, а шестой – в третью корзину и так далее (в третьей корзине накапливается 7 шариков, в четвертой 8 ...).

Часы проработали T секунд. Они должны работать еще P секунд. Требуется определить минимальное количество шариков в большой корзине в момент времени Т, необходимое для успешной работы часов в течение этих P секунд.

Входные данные: T и P (T0, P0, T+P<=1 000 000 000).

Выходные данные: количество шаров.

Пример:

Входные данные: 0 32

Ответ: 10

10. Есть N лампочек и M переключателей, каждый из которых какие-то лампочки переключает, а какие-то нет. Сначала часть лампочек включена. Договоримся горящие лампочки обозначать 1, а выключенные – 0. Для переключателей будем писать 1, если переключатель меняет состояние данной лампочки, и 0, если не меняет. Тогда любой переключатель можно представить строкой из N нолей и единиц. Начальное и конечное состояние лампочек также закодируем строкой из 0 и 1. «Применение» переключателя к лампочкам приводит к тому, что включенные лампочки становятся выключенными, а выключенные – включенными (естественно, это справедливо только для лампочек, к которым есть доступ от этого переключателя). Напишите программу, которая определяет, какие переключатели нужно применить, чтобы лампочки перешли в конечное состояние.

Входные данные:

Вводятся числа N и M (1<=N<=50, 1<=M<=50).

Вводится строка, характеризующая начальное состояние лампочек.

Вводится строка, характеризующая конечное состояние лампочек.

Вводится M строк, характеризующих переключатели.

Выходные данные: Номера переключателей, которые нужно применить, причем каждый переключатель можно применить не более 1 раза, либо сообщение «Нет решения».

Пример:

Входные данные:

5 3

10010

11000

11100

10001

10110

Выходные данные:

1 3

СОДЕРЖАНИЕ

ПРЕДИСЛОВИЕ 3

1. ОБЩАЯ ХАРАКТЕРИСТИКА НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЙ РАБОТЫ СЛУШАТЕЛЕЙ ПЕРЕПОДГОТОВКИ ПЕДАГОГИЧЕСКИХ КАДРОВ 4

2. РЕКОМЕНДАЦИИ ПО РАБОТЕ С ЛИТЕРАТУРНЫМИ ИСТОЧНИКАМИ 7

3. НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СЛУШАТЕЛЕЙ В ПЕРИОД СЕССИИ 10

4. НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА СЛУШАТЕЛЕЙ В МЕЖСЕССИОННЫЕ ПЕРИОДЫ

4.1. Методика подготовки и оформления контрольной работы 15

4.2. Методика подготовки и оформления реферата 17

4.3. Методика подготовки и оформления курсовой и дипломной работы 21

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА 34

ПРИЛОЖЕНИЯ

Приложение 1. Учебная программа по дисциплине «Методология научного исследования» 36

Приложение 2. Задания на межсессионный период для слушателей

специальности «Информатика» 40

Учебное издание

Андарало Александр Иванович

Климович Анна Федоровна

Логинова Инна Николаевна и др.

НАУЧНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА

СЛУШАТЕЛЯ ПЕРЕПОДГОТОВКИ

ПЕДАГОГИЧЕСКИХ КАДРОВ

Учебно-методическое пособие

48