8.5.3 Идентификация закона распределения при помощи критерия согласия

T_j=

Определяем теоретическую дифференциальную функцию распределения для каждого класса по формуле

Нормальное распределение

P*( )=

Распределение Лапласа

P*( )=

Определение дифференециальных функций для экспоненциальных

распределений.

P_j(X_j)=P_j(t_j)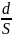

Для закона распределения Симпсона

За и примем точки пересечения с осью абсцисс полигона,

т.е =48,21мА, мА

После расчета функции P_j(X_j) для всех законов распределения определяем теоретическую частоту для всех классов и заполняем таблицу 8.3

E_j= P_j(X_j)n.

Определяем величину χ²

χ²=

Для удобства расчета сводим все в таблицу 8.3. Находим что для нормального распределения χ²=5,6548, распределения Лапласа χ²=16,0615 ,а для распределения Симпсона χ²=22,5304 .Чем меньше χ², тем больше подходит распределение.

Далее определяем число степеней свободы эмпирического ряда

v=m-1-r,

v=7-3=4

По таблице П5, в соответствии с значением v, определяем строку и по строке смотрим , какая из цифр vнаиболее близко к значению χ², определяем столбец и вероятность согласия эмпирического и теоритического распределений. Таким образом, вероятность согласия для нормального закона распределения Р 0,95; Лапласа Р=0;Симпсона Р=0. Наиболее подходящим из анализируемых распределений является нормальное распределение (ЗНР).

8.6.Определение погрешности измерений

Определяем границы доверительного интервала случайной погрешности измерений:

=±t_p

где t_p – квантиль распределения

Для нормального распределения, если n 30 при Р=0,9 t_0,9=1,64,при Р=0,95 t_0,95=1,96, при Р=0,99 t_0,99=2,58. Для распределения Лапласа при Р=0,99 t_0,9=1,38, при Р=0,95 t_0,95=1,87. Для распределения Симпсона - =±2,4S ,

В нашем примере

=±1,96* =± 0,14112 мА

Далее определяем доверительные границы не исключённой систематической погрешности .

В качестве границ не исключенной систематической погрешности принимаем погрешности изготовления меры =±0,9мА.

Определяем доверительные границы суммарной погрешности результата измерения зависят от соотношения

Если 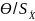<8, то границы погрешности результата измерения принимаются равными случайной погрешности, _∑=

Если , то границы погрешности результата измерения принимаются равными случайной погрешности, _∑= ϴ

Если0,8 , то границы погрешности результата измерения определяют по формуле _∑=KS_∑

K

Для нашего примера

_∑= ϴ=0,9мА

Результат измерения записываем в виде

Q= ± , при P=0,9% ,n=100

A= (100,0±0,9) , при P=0.9% ,n=100

8.7. Определение числа измерений для частичного и полного исключения случайной погрешности

При использования однократного наблюдения (n=1) =0,75 Н ,тогда =0,9/0,75=1,2 т.е на результат однократного измерения оказывает влияние случайная погрешность . Число измерений для исключения определяем следующим образом.

Для частичного исключения

n_ч=

n_ч= (0,8*0,75)²/0,9=0,44

Для полного

n_п=

n_п= (8*0,75)²/0,9=44,44

Для нашего примера при n_ч≥1,47 , принимаем 2 ; при n_п≥ 147,5, принимаем 150