2.3.Проектный расчет передачи

Межосевое расстояние определяем из условия контактной прочности:

= (u + 1) ,

где - коэффициент вида передачи, = 410

K_Н - коэффициент контактной нагрузки, предварительно примем K_Н =1.2.

Коэффициент ширины зубчатого венца = 0.4 (ряд на с. 11 [1]).

Расчетное межосевое расстояние

= 410(4 + 1) = 120 мм

Округлим до ближайшего большего стандартного значения (табл. 6.1 [1]).

= 125 мм

Модуль выберем из диапазона (для непрямозубых передач стандартизован нормальный модуль m_n)

m = = = 1.25…2.5 мм

Округлим m до стандартного значения (табл. 5.1 [1]): m = 2 мм

Суммарное число зубьев

Z = ,

где = для шевронных передач.

Z = = 122.25

Значение Z округлим до ближайшего целого числа Z = 122

Уточним для косозубых и шевронных передач делительный угол наклона зуба

β= arccos = arccos = 11º6’46”

Число зубьев шестерни

Z₁= = = 24.4

Округлим до ближайшего целого числа Z₁ =24

Число зубьев колеса

Z₂= Z – Z₁ = 122-24 = 98

Фактическое передаточное число

u_ф = = = 4.08

Значение u_ф не должно отличаться от номинального более чем на 2.5 % при u 4.5 и более чем на 4 % при u > 4.5.

u = 100 = 100 = 2 %

Коэффициенты смещения шестерни и колеса: x₁= 0 x₂= 0

Ширина венца колеса

b_w2= = 0.4∙125 = 50 мм

Округлим b_w2 до ближайшего числа из ряда на с. 14 [1].

Ширину венца шестерни b_w1 примем на 3 мм больше чем b_w2:

b_w1= 50 + 3 = 53 мм

Определим диаметры окружностей зубчатых колес, принимая далее для непрямозубых колес m = m_n.

Диаметры делительных окружностей для косозубых колес :

d₁ = 49.1 мм d₂ = 200 мм

Диаметры окружностей вершин при x = 0: d_aj = d_j + 2m(1 + x_j):

d_a1 = 53.1 мм d_a2= 200.4 мм

Диаметры окружностей впадин d_fj = d_j – 2m(1.25 – x_j):

d_f1 = 44.1 мм d_f2 = 195 мм

Вычислим окружную скорость в зацеплении

V = = = 3.09 м/с

Степень точности передачи выбираем по табл. 8.1 [1] в зависимости от окружной скорости в зацеплении: n_ст= 8

2.4. Проверочный расчет передачи

Условие контактной прочности передачи имеет вид _.

Контактные напряжения равны

= ,

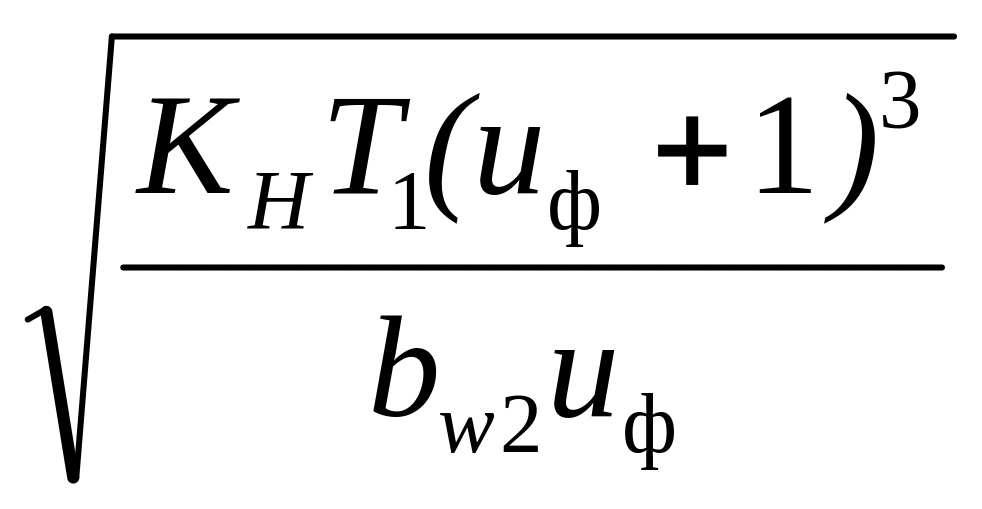где Z_σ- коэффициент вида передачи, Z_σ = 8400

K_Н - коэффициент контактной нагрузки,

K_Н = K_Hα K_Hβ K_НV.

Коэффициент неравномерности распределения нагрузки между зубьями

K_Hα =1+ A (n_ст – 5) K_w = 1.13

где А = 0.15 для косозубых передач;

K_w - коэффициент, учитывающий приработку зубьев.

При НВ₂ < 350

K_w = 0.002НВ₂ + 0.036(V – 9) = 0.002∙248.5+0.036(3.09-9) = 0,289

Коэффициент неравномерности распределения нагрузки по ширине колеса

K_Hβ =1+ (K – 1) K_w,

где K - коэффициент распределения нагрузки в начальный период работы, определяемый по табл. 9.1 [1] в зависимости от коэффициента ширины венца по диаметру.

= 0.5 (u + 1)= 0.5∙0.4(4+1) = 1

K = 1.05 K_Hβ = 1.014

Динамический коэффициент определим по табл. 10.1 [1]

K_НV=1.065

Окончательно получим

K_H=1.3∙1.014∙1.065=1.22

Расчетные контактные напряжения

= = = 481 МПа

Допускается перегрузка по контактным напряжениям не более 5%, рекомендуемая недогрузка до 15%. Расчет перегрузки или недогрузки выполним по формуле

=100 = 100 = -2.6 %

Условия изгибной прочности передачи имеют вид _Fj _FPj.

Напряжение изгиба в зубьях шестерни

,

где Y_Fj  коэффициенты формы зуба;

K_F - коэффициент нагрузки при изгибе;

Y_  коэффициент, учитывающий влияние угла наклона зуба на его прочность: Y_= 1- = 0.889

Напряжение изгиба в зубьях колеса

.

Коэффициенты формы зуба

Y_Fj=3.47 + + 0.092 ,

где Z_Vj - эквивалентное число зубьев, для непрямозубых передач Z_Vj = .

Z_V1 = = = 25,8 Z_V2 = = = 105,3

Y_F1 = 3.47 + = 3.98 Y_F2 = 3.47 + = 3.6

Коэффициент торцевого перекрытия

Ɛα=[1.88-3.2(1/Z1 + 1/Z2)]·cosβ= [1.88-3.2(1/24 +1/98)]·cos11º6’46”=1.672

Коэффициент, учитывающий перекрытие зубьев

ҮƐ=1/Ɛα= 1/1.672=0.6

Коэффициент нагрузки при изгибе

K_F = K_Fα K_Fβ K_FV.

Коэффициент неравномерности распределения нагрузки между зубьями

K_Fα =1+0.15(nст -5)=1.45

Коэффициент неравномерности распределения нагрузки по ширине колеса

K_Fβ = 0.18 + 0.82K = 0.18 + 0.82∙1.05 = 1.041

Динамический коэффициент при НВ₂ < 350

K_FV = 1+ 3(K_HV – 1) = 1 + 3(1.065-1) = 1.195

K_F = K_Fα K_Fβ K_FV = 1.45∙1.041∙1.195 = 1.8

Напряжения изгиба

_F1= = 77.2 МПа

_F2= = 74 МПа

2.5. Силы в зацеплении

Окружная сила F_t = = = 2674.3 Н

Распорная сила F_r = F_t = 2674.3 = 997.2 Н

Осевая сила F_а = tgβ· F_t = 2674.3 · 0.196=524 Н