Закон збереження енергії в механіці.

Розглянемо систему, що складається із N матеріальних точок масами m_i, які рухаються відповідно з швидкостями 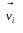, де і=1,2,...,N. У загальному випадку на кожну матеріальну точку системи діють як внутрішні консервативні та неконсервативні сили, так і зовнішні консервативні та неконсервативні сили. 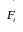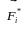Позначимо через рівнодійну всіх консервативних (внутрішніх і зовнішніх) сил, які діють на i-ту точку, а через рівнодійну всіх неконсервативних (внутрішніх і зовнішніх) сил. Запишемо рівняння другого закону Ньютона для і-ї матеріальної точки: 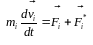(3.29)

Під дією сил кожна із матеріальних точок за проміжок часу dt здійснює переміщення і змінює свою швидкість. Рівняння (3.29) помножимо скалярно на відповідне переміщення :

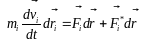
Записавши це рівняння для кожної з матеріальних точок і почленно додавши ці рівняння, отримаємо

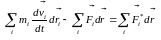(3.30) Перетворимо ліву частину цієї рівності. Враховуючи, що 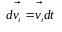і скалярний добуток колінеарних векторів 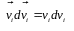, знаходимо, що перша сума дорівнює зміні кінетичної енергії всієї системи за проміжок часу dt:

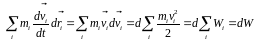
Друга сума, як взята з оберненим знаком сумарна робота всіх діючих в системі консервативних сил за цей час, дорівнює зміні потенціальної енергії взаємодії матеріальних точок між собою і з зовнішнім полем консервативних сил:

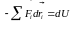
Тоді dW + dU=dE і рівняння (3.30) набуває вигляду 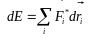(3.31)

Таким чином, зміна повної механічної енергії системи дорівнює сумарній роботі всіх діючих на матеріальні точки неконсервативних внутрішніх і зовнішніх сил.

Якщо система рухається в полі тільки консервативних сил, то 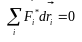і з виразу (3.31) випливає, що dE=0, або E=W + U=const (3.32)

Повна механічна енергія системи, на яку діють тільки консервативні (і гіроскопічні) сили, зберігається, тобто не змінюється з часом.

Це положення називається законом збереження, механічної енергії. У консервативній системі потенціальна і кінетична енергії можуть перетворюватись одна в одну, але в будь-який момент часу їхня сума залишається сталою.

Закон збереження моменту імпульсу

Закон збереження моменту імпульсу справджується в системах, які рухаються під дією центральних зовнішніх сил. Центральними називаються сили, лінії дії яких виходять з однієї точки О. Цю точку називають силовим центром. У будь-якій точці центрального силового поля момент сили відносно силового центра дорівнює нулю, оскільки сила напрямлена вздовж радіуса-вектора, проведеного в цю точку із центра поля. Тому головний вектор моментів зовнішніх центральних сил відносно центра поля також дорівнює нулю. Отже, повний момент імпульсу системи матеріальних точок, яка рухається в центральному силовому полі, відносно силового центра залишається сталим.

Розглянемо рух окремої матеріальної точки масою m у полі центральних сил. Нехай у момент часу t радіус-вектор матеріальної точки, проведений із силового центра, дорівнює 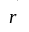, а її швидкість 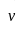. За наступний проміжок часу dt радіус-вектор зміниться на 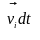і опише нескінченно малу площу dS трикутника (на рис. 2.7 заштрихований).

В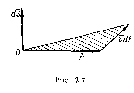 изначимо цю площу як модуль осьового вектора 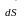, перпендикулярного до площини трикутника:

Похідну 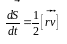(2.54) називають секторною швидкістю, її числове значення дорівнює площі, описаній радіусом-вектором за одиницю часу. За означенням момент імпульсу матеріальної точки відносно центра поля , або з врахуванням (2.54) 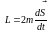(2.55)

Оскільки момент центральної сили відносно силового центра дорівнює нулю, то момент імпульсу 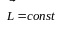. При повільних (нерелятивістських) рухах маса матеріальної точки не змінюється з часом і вираз (2.55) перетворюється в закон площ: 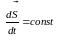(2.56)

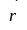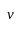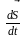Із формули (2.54) випливає, що площина, в якій лежать вектори і , завжди перпендикулярна до вектора . Іншими словами, траєкторією матеріальної точки в полі центральних сил є плоска крива. Закон площ (2.56) стверджує, що радіус-вектор матеріальної точки за однакові проміжки часу описує рівні за розміром площі.

Закон збереження моменту імпульсу в замкнених механічних системах с окремим випадком фундаментального закону збереження моменту імпульсу. У фізиці поняття моменту імпульсу розширюється, ця характеристика властива не тільки частинкам речовини, а й силовим полям. Узагальнений закон збереження моменту імпульсу постулюється на всі фізичні процеси.