3 Питання

7 білет

1 Питання

Вивчення явища електромагнітної індукції показало, що зміна магнітного поля, в якому знаходиться провідний контур, викликає появу в цьому контурі індукційного (вихрового) електричного поля. Максвелл розвинув уявлення Фарадея про електромагнітну індукцію, довівши, що вихрове електричне поле з'являється в довільній частині простору, де існує змінне магнітне поле (незалежно від того, чи є там провідники, чи немає). А в середині 60-х років ХІХ ст. Максвелл дійшов висновку, що існує і зворотний процес: змінне електричне поле викликає появу змінного магнітного поля (вихрового). Отже, магнітне поле може створюватися не тільки електричним струмом (тобто рухомими електричними зарядами), але і змінним електричним полем (рис.5.2.15).

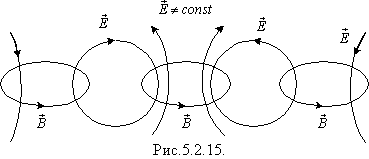
Сукупність нерозривно взаємопов'язаних змінних вихрових електричного і магнітного полів називають електромагнітним полем. У природі взагалі немає відокремлених одне від одного електричних і магнітних полів, а існують електромагнітні поля як особливий вид матерії, через який відбувається електромагнітна взаємодія.

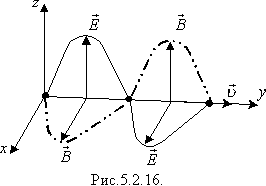
Процес поширення змінного електромагнітного поля в просторі з плином часу називають електромагнітною хвилею. Максвелл показав, що швидкість поширення електромагнітної хвилі є величиною скінченною і у вакуумі дорівнює швидкості світла (тобто c   3·10⁸ м/с). Електромагнітні хвилі є поперечними, оскільки в кожній точці простору електрична напруженість , магнітна індукція і швидкість поширення цих хвиль взаємно перпендикулярні (рис.5.2.16). Із теорії Максвелла випливає, що швидкість поширення електромагнітної хвилі у речовині визначається за формулою

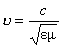,                    (5.2.7)

де c - швидкість електромагнітних хвиль у вакуумі; e - діелектрична проникність; m - магнітна проникність середовища. Із формули (5.2.7) видно, що швидкість поширення електромагнітної хвилі в середовищі залежить від електричних і магнітних властивостей цього середовища.

Відстань, на яку поширюється електромагнітна хвиля за один період, тобто найкоротша відстань між таким двома точками хвилі, в яких і коливаються в однакових фазах, називають довжиною електромагнітної хвилі і позначають через l. За аналогією з механічними хвилями:  = ln = l /  T, де T - період, n - частота електромагнітних коливань. Із теорії Максвелла випливає, що довільний заряд, що рухається із прискоренням або коливається, випромінює електромагнітні хвилі.

Електромагнітна хвиля поширюється в діелектрику, але ще краще у вакуумі. Наявність прискорення - головна умова випромінювання електромагнітної хвилі.

У вакуумі електромагнітні хвилі досягають найбільшої швидкості - швидкості світла (c = 3·10⁸ м/с). Властивості електромагнітних хвиль найлегше вивчати, використовуючи передавач і приймач, які працюють на сантиметровому діапазоні. Випромінювання і приймання таких хвиль можна зробити спрямованими. Досліди Герца і пізніше проведені експерименти показали, що електромагнітні хвилі мають такі властивості:

1) в однорідному середовищі поширюються рівномірно і прямолінійно;

2) відбиваються діелектриками, а ще краще провідниками, при цьому виконуються закони відбивання хвиль;

3) заломлюються;

4) фокусуються;

5) дають явища дифракції і інтерференції;

6) поляризуються.

Хвильове рівняння

Хвильове́ рівня́ння — рівняння, яке описує розповсюдження хвиль у просторі.

Хвильове рівняння є зазвичай рівняння другого порядку у часткових похідних гіперболічного типу, хоча існують хвильові рівняння інших порядків та інших типів.

У одномірному випадку хвильове рівняння записується.

,

де u — невідома функція, яка описує хвилю, x — просторова координата, t — час, s — фазова швидкість поширення хвилі.

Розв'язки

Хвильові рівняння мають багато можливих розв'язків. Реалізація того чи іншого із них залежить від граничних та початкових умов: від того, як хвиля народилася, які перешкоди зустрічає на своєму шляху, тощо.

Загальний розв'язок хвильового рівняння подається суперпозицією функцій типу

,

де u₀ — амплітуда хвилі, k — хвильове число, ω — циклічна частота,  — фаза хвилі.

Хвильове число та частота зв'язані між собою дисперсійним співвідношенням

Ефект Доплера — явище зміни частоти хвилі, яка випромінюється рухомим джерелом.

,

де ν частота хвилі, яку фіксує нерухомий спостерігач, ν₀ — частота коливань у рухомому джерелі, s — швидкість розповсюдження хвилі, v — швидкість джерела. Знак залежить від напрямку руху джерела відносно спостерігача.

Частота хвилі, яку фіксує спостерігач зростає, якщо джерело рухається до нього, й зменшується, якщо джерело рухається від спостерігача.

Використання

Ефект Доплера використовується в радіолокації для розпізнавання рухомих об'єктів, наприклад, літаків, на фоні нерухомих (гір, хмар). За червоним зміщенням світла від астрономічних об'єктів, вимірюється їхня швидкість і розраховується віддаль до них. Ефект Доплера широко використовується в медицині. На базі ефекту створені компютерні комплекси ультразвукової доплелографії. Зміна характеристик ультразвуку при проходженні через судини дозволяє визначати стан кровотоку, як в поверхневих так і у внутрішніх судинах.

Шкала електромагнітних хвиль

Довжина, м	Частота, Гц	Найменування
106-104	3∙102-3∙104	Наддовгі
104-103	3∙104-3∙105	Довгі (радіохвилі)
103-102	3∙105-3∙106	Середні (радіохвилі)
102-101	3∙106-3∙107	Короткі (радіохвилі)
101-10-1	3∙107-3∙109	Ультракороткі
10-1-10-2	3∙109-3∙1010	Телебачення (НВЧ)
10-2-10-3	3∙1010-3∙1011	Радіолокація (НВЧ)
10-3-10-6	3∙1011-3∙1014	Інфрачервоне випромінювання
10-6-10-7	3∙1014-3∙1015	Видиме світло
10-7-10-9	3∙1015-3∙1017	Ультрафіолетове випромінювання
10-9-10-12	3∙1017-3∙1020	Рентгенівське випромінювання (м'яке)
10-12-10-14	3∙1020-3∙1022	Гамма-випромінювання (жорстке)
≤10-14	≥3∙1022	Космічні промені

Теорія Максвелла розглядає поля, що створюються макроскопічними зарядами та струмами, рівномірно розподіленими в об'ємах, що є значно більшими від характерних об'ємів атомів і молекул речовини, на відстанях від джерел значно більших за атомні розміри. Зміни полів розглядаються в часових інтервалах, значно більших від характерних часових інтервалів атомних процесів (наприклад, періоду обертання електронів на орбітах навколо ядер). Принципово важливою особливістю електричних і магнітних полів є наявність тісного взаємозв'язку між ними.

Система рівнянь Максвелла є узагальненим математичним записом основних експериментальних законів електромагнітних явищ у довільному середовищі. Ці рівняння становлять основу розробленої Дж. Максвеллом теорії макроскопічної електродинаміки. Рівняння Максвелла встановлюють співвідношення між векторами електромагнітного поля Е, В, D і Н та розподілом у просторі їх джерел: електричних зарядів і струмів. Обмеження, які накладаються на застосовність цих рівнянь, такі: тіла, вміщені в поле, є нерухомими; параметри , та , які характеризують властивості речовини в кожній точці, є незмінними в часі і не залежать від температури та напруженості зовнішнього поля; в полі немає постійних магнітів, сегнетоелектриків та феромагнетиків.

В інтегральній формі система рівнянь Максвелла записується так:

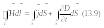
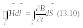
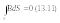
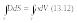
а у диференціальній –

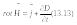
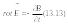
Перше рівняння Максвелла – це узагальнення закону Біо – Савара – Лапласа і є більш загальною формою закону повного струму, який відображає той експериментальний факт, що джерелами вихрового магнітного поля можуть бути струми провідності і струми зміщення.

Друге рівняння Максвелла є математичним записом експериментального закону електромагнітної індукції Фарадея. Узагальнений фізичний зміст його полягає в тому, що всяка зміна в часі магнітного поля спричиняє збудження вихрового електричного поля.

Третє рівняння Максвелла відображає експериментальний факт відсутності в природі магнітних зарядів, тобто відсутність джерел магнітного поля, подібних до джерел електричного поля (зарядів).

Четверте рівняння Максвелла є узагальненням на основі теореми Гаусса закону Кулона і фізично вказує на існування в природі джерел електричного поля у вигляді електричних зарядів, розподілених у просторі з об'ємною густиною .

Як видно, рівняння Максвелла не є симетричними відносно електричного і магнітного полів. Це зумовлено наявністю в природі джерел електричного поля (електричних зарядів) і відсутністю подібних джерел магнітного поля (магнітних зарядів, монополів).

До матеріальнихОшибка! Закладка не определена. рівнянь належать рівняння, що зв'язують індукцію та напруженість електричного поля

                     (26)

через діелектричну проникливість середовища e та магнітного поля

                     (27)

через магнітну  проникливість .

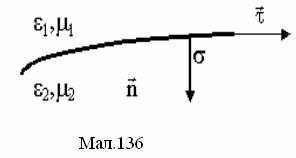
Граничні умови визначають напруженість та індукцію електричного та магнітного поля при переході з одного середовища з  проникливістями та  в інше середовище з проникливістями  та  . Граничні умови для індукції  та напруженості  магнітного поля установлюються подібно граничним умовам для індукції  та напруженості електричного поля , а тому граничні умови приведемо без доведення.   Нехай на границі  ¾ поверхнева густина зарядів,  ¾ одиничний вектор нормалі до поверхні розділу середовищ,  ¾ одиничний вектор, дотичний до поверхні розділу середовищ,   ¾ вектор лінійної густини поверхневого струму провідності.  В цьому випадку рівняння на границі будуть такими: залишаються неперервними тангенціальна складова напруженості електричного поля  та нормальна складова індукції магнітного поля . Нормальна складова індукції електричного поля має стрибок рівний

, а тангенціальна складова напруженості магнітного поля має стрибок рівний  

H_2t - H_1t = .

Вектор  має напрямок по дотичній до поверхні і чисельно дорівнює 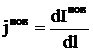, де  сила струму провідності, що проходить через малу дільницю довжиною dl перерізу поверхні, проведеного ^ напрямку поверхневого струму.