Глава 1.Взаимодействие биополимеров с лигандами и между собой

Практически все процессы в живой клетке начинаются с взаимодействия биополимеров с низкомолекулярными лигандами или с взаимодействия биополимеров друг с другом. Образование комплекса является сигналом к последующему биохимическому действию — ответу системы. Так, взаимодействие фермента с субстратом (образование фермент-субстратного комплекса) приводит к превращению субстрата в продукты реакции, а узнавание гормона рецептором — к протеканию определенных внутриклеточных процессов. В подавляющем большинстве случаев экспериментально удается регистрировать именно этот «ответ» системы. Как правило, взаимодействие специфического лиганда с биополимером не сопряжено с преодолением существенных энергетических барьеров и является быстрым процессом. Поэтому исследователи имеют дело с равновесными процессами, требующими термодинамического подхода. Ниже мы рассмотрим некоторые простые случаи взаимодействия биополимеров с лигандами.

1.1.Термодинамика взаимодействия биополимеров с лигандами

Как уже было сказано выше, в большинстве случаев не удается измерить концентрации всех компонентов равновесия. Как правило, известны начальные концентрации биополимера и лиганда и отклик («ответ») биологической системы. Константы равновесия, рассчитанные из этих данных, являются эффективными (кажущимися) и их физический смысл изначально не определен. Придать им физический смысл можно лишь в рамках определенной термодинамической модели

Ниже мы рассмотрим некоторые простые термодинамические модели, широко используемые для описания взаимодействия биополимеров с лигандами.

1.1.1.Взаимодействие биополимеров с недостатком лиганда

Одно место связывания

В некоторых особых случаях (например, при взаимодействии с ДНК или олигонуклеотидами интеркалирующих¹ красителей) вследствие существенного отличия физических свойств связанного и несвязанного лигандов удается экспериментально измерить концентрацию связанного лиганда [L_b], а. Следовательно, и концентрацию не прореагировавшего, свободного лиганда [L_f] ([L_f] = [L]_o – [L_b], где [L]_o — исходная концентрация лиганда). Такой случай описывается, как правило, с помощью модели Скетчарда.

( 4.0)

где P — биополимер, а PL — его комплекс с лигандом.

Константа равновесия

( 4.0)

Учитывая, что [PL] = [L_b], а [P] = [P]_o – [PL] = [P]_o – [L_b], получим:

Рис. 4.1. Кривая связывания лиганда биополимером, имеющим одно место связывания. Кружки — экспериментальные данные, сплошная кривая — результат нелинейной регрессии (фиттинга) этих данных по уравнению ( 4 .0) При повышение концентрации лиганда [L_b] асимптотически приближается к [P]_o (насыщение всех мест связывания).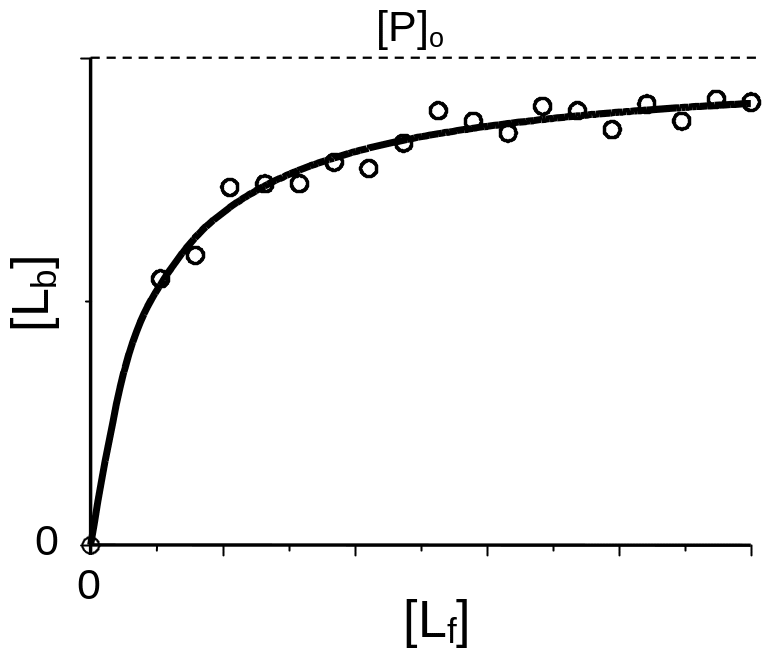

( 4.0)

( 4.0)

Уравнение ( 4 .0) представляет собой гиперболическую зависимость, проходящую через начало координат (Рис. 4 .1). При повышении концентрации лиганда концентрация связанного лиганда асимптотически стремится к [P]_o.

На практике для анализа связывания чаще используют линейную анаморфозу уравнения ( 4 .0):

( 4.0)

принято называть уравнением Скетчарда. В случае биополимера с одним местом связывания уравнение Скетчарда дает прямую линию, тангенс угла наклона которой равен –K (Рис. 4 .2).

N одинаковых независимых мест связывания

Часто встречается ситуация, когда биополимер имеет не одно, а несколько мест связывания. Если эти места одинаковы и не зависят друг от друга (связывание одной молекулы лиганда не влияет на константу связывания следующей молекулы лиганда), то общие закономерности связывания мало отличаются от рассмотренных в предыдущем разделе.

Рис. 4.2. Те же данные, что и на предыдущем рисунке, но представленные в виде графика Скетчарда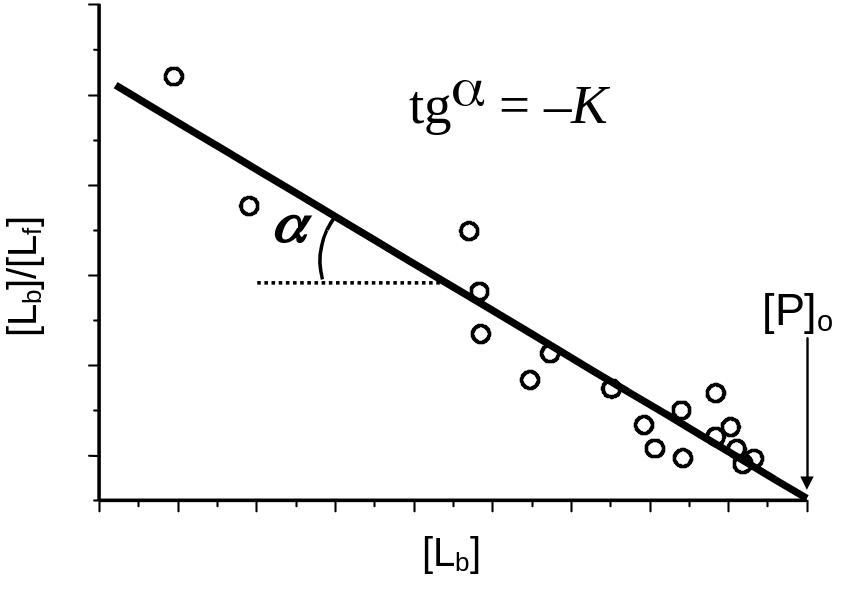

В этом случае [P] и [PL] имеют смысл концентрации свободных и занятых мест связывания, соответственно, а вместо величины [P]_o следует использовать произведение n[P]_o, где n — число мест связывания, приходящееся на одну молекулу биополимера. Тогда уравнения связывания и Скетчарда преобразуются к виду:

( 4.0)

( 4.0)

Так же как и в предыдущем разделе, кривая связывания представляет собой гиперболу, а график Скетчарда — прямую линию. Отличие заключается лишь в том, что кривая связывания стремится не к [P]_o, а к n, а прямая Скетчарда отсекает на оси абсцисс отрезок, равный n.

Два типа независимых мест связывания

Нередко биополимер обладает несколькими типами мест связывания, различающихся сродством к лиганду (разной константой связывания). В простейшем случае двух типов независимых мест связывания кривая связывания описывается суммой двух гипербол (при трех типах мест связывания — суммой трех гипербол и т.д.) (уравнение ( 4 .0):

( 4.0)

Рис. 4.3. Графика Скетчарда для случая связывания лиганда с биополимером, имеющим два типа независимых места связывания.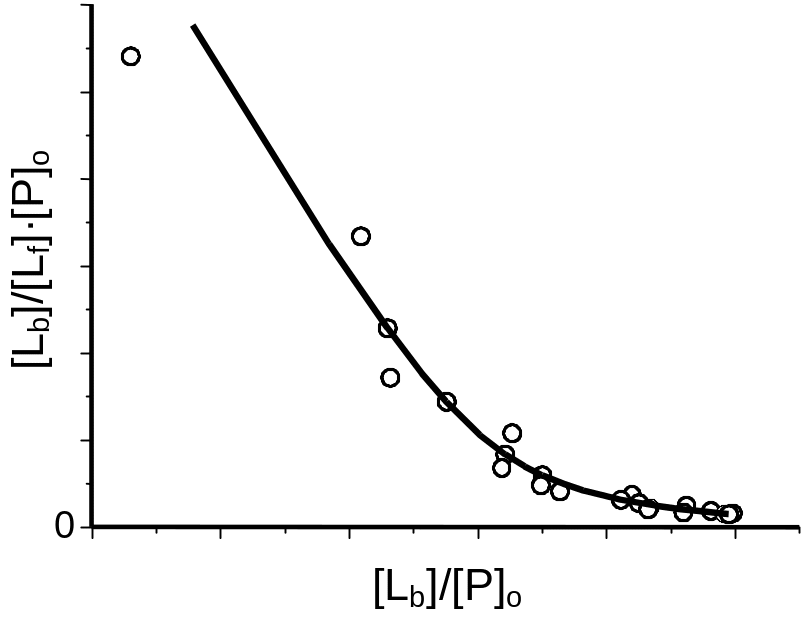

Уравнение Скетчарда для связывания лиганда биополимером, имеющим два и более типов связывающих мест, выглядит достаточно сложно и я не буду здесь его приводить. На Рис. 4 .3 представлен график Скетчарда для таких систем. Для нас важно, что этот график уже не является прямой линией, а представляет собой вогнутую кривую.

Вообще говоря, линейные анаморфозы и, в частности, график Скетчарда дают менее точные и достоверные результаты, чем непосредственно нелинейная регрессия экспериментальных данных. Однако предварительный анализ таких графиков может быть весьма полезен для выяснения типа связывания и оценки величины начальных параметров для нелинейной регрессии.

Остается вопрос: можно ли так же хорошо описать экспериментальные данные, предполагая наличие у макромолекулы более, чем двух типов мест связывания? Конечно, большее число параметров позволяет подогнать к модели любые данные и получить более хорошее соответствие между расчетом и экспериментом. Однако для объяснения результатов (в пределах экспериментальной ошибки) лучше всего использовать наиболее простую модель. Такой подход дает возможность описать систему минимальным (и, по-видимому основным) числом параметров.

В заключение следует сказать, что вогнутая кривая Скетчарда характерна не только для макромолекул с двумя или большим числом типов мест связывания, но и для антикооперативного связывания лиганда. Проблемы кооперативного связывания мы рассмотрим ниже.