Глава 3 Элементы алгебры логики. Обработка логической информации
.
3.1 Логические переменные
a, b, c x, y, z простые переменные ( высказывания)
A, B, C X, Y, Z сложные логические высказывания
b – истина b = 1
d – ложно d = 0
A(b, c, d, …)
При фиксированном значении истинности простых высказываний сложное высказывание может принять только одно из двух значений.
A(b, c, d, …) = (1 или 0)
b = 1
c = 0 A(b, c, d) = 1
d = 1
Аналогично по форме сложных высказываний записывается логическая функция
F(a, b, c),которая может принимать фиксированное число значений:
K = 23 = 8
a |
b |
F1 |
F2 |
F3 |
F4 |
F5 |
F6 |
F7 |
F8 |
F9 |
F10 |
F11 |
F12 |
F13 |
F14 |
F15 |
F16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
3.2 Символы логических операций (логические связки)
Таблица 3.1
F1(a, b)= - логический ноль
F2(a, b)=a&b конъюнкция (a И b)
Конъюнкция – это логическая операция, которая истинна, если истинны составляющие её простые высказывания и ложна в остальных случаях.
3.2.1 Свойство поразрядности логических операций.
Все логические операции относятся к поразрядным, то есть результат применения к операндfм логических связок зависит только от информации в одноименных разрядах многоразрядных операндов.
А=100111
&
В=110011
A&B=100011
A=1001
&
B=1111
&
C=0101
&
D=1011
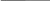A&B&C&D=0001
F8(a, b)=avb дизъюнкция (a ИЛИ b)
Дизъюнкция – это логическая операция, которая ложна, если ложны составляющие её простые высказывания и истинна в остальных случаях.
F11(b)=ıb=b¯ - операция отрицания операнда b (НЕ b)
Совокупность логической операции составляет основной базис для которого справедливы законы Булевой алгебры.
F9(a, b)=a b=ı(avb) - стрелка Пирса.
F15(a, b)=a/b=a&b / - штрих Шеффера.
и / (стрелка Пирса и штрих Шеффера) представляют собой самостоятельные логические базисы (ИЛИ – НЕ, И – НЕ) , которые позволяют любое сложное высказывание (логическую функцию) записать с использованием только одной логической связки.
F10(a, b)=a~b=(ā&ıb)v(a&b)
~ - знак эквивалентности
, mod2 - сумма по модулю 2.
- прямая импликация
a - антицедент
b - консеквент
F3(a, b)=ı(ab)=ı(ıavb)
Логические функции двух переменных a и b позволяют сформулировать некоторые базисы , на основе которых стоят логические схемы при синтезе любых цифровых обработчиков информации.
Примерами таких базисов являются:
&, v,ı (И, ИЛИ, НЕ)
&,ı И – НЕ
v,ı ИЛИ – НЕ
, mod2 - сумма по модулю 2.
- прямая импликация
~ - знак эквивалентности
/ - штрих Шеффера.
- стрелка Пирса.
3.3 Законы алгебры логики.
Большенство законов алгебры логики являются двойственными по отношению к операциям конъюнкция и диpъюнкция и представляют собой некоторые эквивалентности ,справедливость которых может быть доказана заданием всех значений истинности входящих в них переменных и выполнением над ними требуемых операций
.
Коммутативные законы.
Для конъюнкции: A&B=B&A
Для дизъюнкции: AvB=BvA
Ассоциативные законы.
Для конъюнкции: A&(B&C)=(A&B)&C
Для дизъюнкции: Av(BvC)=(AvB)vC
Дистрибутивные законы
Для конъюнкции: (AvB)&C=(A&C)v(B&C)
Для дизъюнкции: (A&B)vC=(AvC)&(BvC)
(A·B)+C=(A+C)·(B+C)
Таблица истиности, иллюстрирующая доказательство дистрибутивного закона для дизъюнкции для случая трех простых переменных
Таблица 3.2
8экв. |
a |
b |
C |
avb |
(a&b)vc |
avc |
bvc |
(avc)&(bvc) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
2 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
3 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
4 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
6 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
7 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Закон Де Моргана:
Для конъюнкции: ıA&B=ıAvıB
Для дизъюнкции: ı(AvB)=ıA&ıB