Если отсутствует автокорреляция, то парный коэффициент корреляции можно находить по обычной формуле rхy .

Уравнение связи (регрессии) отклонений имеет вид:

(7.30)

В этом уравнении a0 всегда равно 0, коэффициент регрессии a1 вычисляют по формуле:

(7.31)

Ряд авторов предлагает совместить показатели рядов в едином уравнении, т.е. построить многофакторное уравнение, отражающее зависимость результата (У) от фактора (Х) и его изменение во времени (t)

Ỹхt = a0 + a1 х + а2 t (7.32)

Это уравнение отражает зависимость изменений значений одного ряда показателей (У) от изменений значений другого ряда (Х) во времени t. Время t задаётся как натуральный ряд чисел t=1,2,3,…, n или нумерацию производят от середины ряда, как это показано в вопросе 4. Параметры уравнения регрессии можно найти, используя метод наименьших квадратов, если составить и решить следующую систему трех уравнений с тремя неизвестными

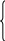(7.33)

Система упростится, если номерацию уровней ряда проводить от его середины так, чтобы t=0. Тогда система примет несколько упрощенный вид:

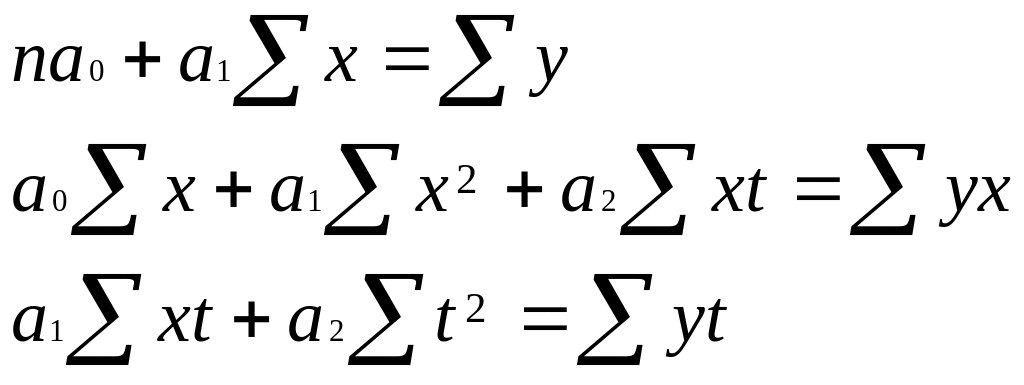(7.34)

Затем исследование проводится также, как в многофакторном корреляционно-регрессионном анализе.

В учебниках по общей теории статистики не отражена проблема построения уравнения регрессии при наличии тренда и при наличии сезонных колебаний.

В 8. Понятия интерполяции и экстраполяции в рядах динамики.

В рядах динамики часто теряется информация при сборе данных для них.

Слово «интерполяция» латинского происхождения (interpolatio) – означает изменение. Современное использование этого слова в экономических науках имеет несколько другой, более широкий смысл.

Интерполяция – это способ определения промежуточных значений динамического ряда:

а) на основе известных соседних значений (как среднее арифметическое);

б) на основе взаимосвязей с другими рядами, количественные выражения которых известны;

в) на основе средних значений показателей ряда динамики (см. вопрос 2).

При проведении интерполяции предполагается, что выявленная тенденция и ее характеристики не претерпели существенных изменений в тот период времени, уровни которого отсутствуют.

При прогнозировании развития анализируемых показателей на перспективу используется метод экстраполяции, при проведении которого предполагается, что условия развития явления в будущем не изменятся. Такая экстраполяция называется перспективной. Чем короче срок экстраполяции, тем точнее и надежнее ее результаты. За короткий срок чаще всего условия развития резко не меняются. Однако история знает и другие примеры, такие как развал Советского Союза и образование целого ряда независимых государств, в т.ч. и Республики Беларусь, финансовый и экономический кризис 2008–200_..гг.

Термин «экстраполяция» произошел от соединения двух латинских слов «extra» – сверх и «polire» – делать гладким. Соединение этих двух терминов в одном слове означает нахождение по ряду известных значений величины данной таблицы или графика других ее значений, находящихся вне ее ряда.

Экстраполяция – это метод определения количественных характеристик для совокупностей, не подвергающихся изучению непосредственно, а на основе изучения предыдущего их развития или развития аналогичных совокупностей.

Чем дальше прогнозирование от реального фактического времени, тем больше интервальная ошибка результатов экстраполяции. Поэтому с течением времени необходимо с учетом свершившегося факта оценивать динамику ряда и осуществлять корректировку прогноза.

По сути дела методика экстраполяции и расчет значений уровня ряда на перспективу рассмотрен нами в вопросе 4 данной темы.

Оба эти метода возможны только в условиях стабильного развития технолого-экономических показателей.