1. Модель развития экономики (модель Харрода)

В модели учитывается один определяемый фактор – капитальные вложения, а состояние экономики оценивается через размер национального дохода. Y_t – национальный доход; K_t – производственные фонды; C_t – объем потребления; S_t – объем накопления; V_t – капитальные вложения. Предположим, что функционирование экономики происходит при следующих условиях: условие баланса доходов и расходов за каждый год: Y_t = C_t + S_t; условие исключения пролеживания капитала: S_t = V_t; условие пропорционального деления национального годового дохода: S_t = a*Y_t.

Два условия принимаются для характеристики внутренних экономических процессов: первое – связь капитальных вложений и общей суммы производственных фондов; второе – связь национального годового дохода и производственных фондов.

Капитальные вложения в год t – прирост производственных фондов: V_t­ = dK/dt. Национальный доход в каждый год – отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи: Y_t = K_t/b.

Y_{t­ =} V_t­/a = dK/(a*dt) = b/a * dY/dt. => уравнение Харрода: b*dY/dt = a*Y. Его решение – экспоненциальное изменение национального дохода по годовым интервалам: Y_t = Y₀*e^at/b.

2. Статистическая модель межотраслевого баланса

Идея сбалансированности лежит в основе всякого рационального функционирования хозяйства. Суть – затраты должны компенсироваться доходами. Балансовый метод – взаимное сопоставление имеющихся ресурсов и потребностей в них. Межотраслевой баланс отражает производство и распределение ВНП в отраслевом разрезе, межотраслевые производственные связи, использование материальных и трудовых ресурсов, создание и распределение трудовых ресурсов и национального дохода.

Производящие отрасли	Потребляющие отрасли		Конечный продукт	Валовый продукт
	1	n
1	x11 (I)	x1n (I)	Y1 (II)	X1
n	xn1 (I)	xnn (I)	Yn (II)	Xn
Амортизация	c1 (III)	cn (III)	(IV)
Оплата труда	v1 (III)	vn (III)
Чистый доход	m1 (III)	mn (III)
Валовый продукт	X1	Xn

Пусть экономика страны имеет n-отраслей материального производства. Каждая отрасль выпускает некоторый продукт, часть которого потребляется другими отраслями (промежуточный продукт), а другая часть – идет на конечное потребление и накопление (конечный продукт). X_i – валовый продукт i-ой отрасли; x_ij – стоимость продукта, произведенного в i-ой отрасли и потребленного в j-ой области для изготовления продукции стоимостью X_j; Y_i – конечный продукт i-ой области.

Межотраслевой баланс состоит из 4 квадрантов: 1 – межотраслевые потоки продукции; 2 – отраслевая материальная структура национального дохода; 3 – национальный доход как стоимость условно-чистой продукции (Z_j) = сумма амортизации (c_j), оплаты труда (v_j) и чистого дохода j-ой отрасли (m_j); 4 – конечное распределение и использование национального дохода.

Валовая продукция j-ой потребляющей отрасли (X_j­) = сумма ее материальных затрат и условно-чистой продукции: 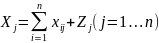. Валовая продукция i-ой производящей отрасли (X_i) = сумма материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли: 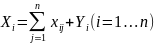. Валовый национальный продукт = сумма валовых продуктов отраслей: 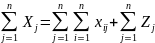; 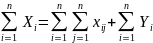. => Должно соблюдаться равенство между итогами 3 и 2 квадрантов: .

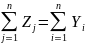Коэффициент прямых затрат (a_ij) – какое количество продукции i-ой отрасли необходимо, учитывая только прямые затраты, для производства единицы продукции j-ой отрасли: a_ij = x_ij / X_j (j = 1…n). => .

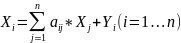A = (a_ij) – матрица коэффициентов прямых затрат; X = (X_i) – вектор-столбец валовой продукции; Y = (Y_i) – вектор-столбец конечной продукции: ЭММ межотраслевого баланса – X = AX + Y – модель Леонтьева (модель «затраты-выпуск»). Эта модель позволяет выполнять 3 варианта расчетов:

1. Задав величины валовой продукции каждой отрасли, можно определить объем конечной продукции каждой отрасли: Y = (E – A)*X.

2. Задав величины конечной продукции всех отраслей, можно определить величины валовой продукции каждой отрасли: X = (E – A)^-1*Y.

3. Задав для ряда отраслей величины валовой продукции, а для всех остальных отраслей задав объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

Для того, чтобы обеспечить положительный конечный выпуск по всем областям необходимо и достаточно, чтобы выполнялось одно из условий: 1. Определитель матрицы (E – A) не равен 0 (существует обратная матрица (E – A)^-1); 2. Матричный ряд E + A + A² +… = 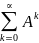сходится и = (E – A)^-1. 3. Наибольшее по модулю собственное значение матрицы A (решение уравнения |λE – A| = 0 строго меньше 1). 4. Все главные миноры матрицы (E – A) положительны.

(E – A)^-1 = B = (b_ij) => для любой i-отрасли: .

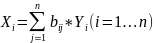Коэффициент полных затрат (b_ij) – какое количество продукции i-ой отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-ой отрасли. Полные затраты отражают использование ресурса на всех этапах изготовления и равны сумме прямых и косвенных затрат на всех предыдущих стадиях производства.

3. Динамическая модель межотраслевого баланса

Основное отличие от статистической – объемы капитальных вложений в каждый год не предполагаются известными, а находятся из модели.

x_i(t) – объем продукции i-ой отрасли; T – продолжительность планового периода; b_ij(t) – капитальные затраты продукции i-отрасли, обеспечивающие увеличение продукции j-ой отрасли на 1; k_ij^r – доля капитальных вложений продукции i-ой отрасли для увеличения продукции j-ой отрасли за r лет до завершения строительства (от всего объема капитальных вложений продукции i-ой отрасли в увеличение продукции j-ой отрасли); τ – период от начала капитальных вложений до получения за их счет дополнительной продукции; y_i’(t) – конечная продукция i-ой отрасли за вычетом затрат и капиталовложений, связанных с расширением производства; Δx_j – изменение продукции j-ой отрасли. 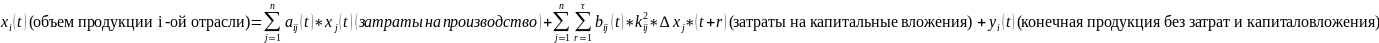. Из этой модели находятся объемы продукции отраслей в каждый год планируемого периода, а также затраты и капитальные вложения в отраслевой и временной структуре.

4. Межпродуктовый баланс

Используется для обеспечения полной взаимоувязки планов производства группы взаимосвязанных предприятий либо группы цехов одного предприятия.

Рассмотрим предприятие, у которого в каждом цехе производится только 1 вид продукции в объеме X_i (i = 1…n). Отдельный вид продукции может быть использован как промежуточный продукт, идущий на внутреннее потребление, и как конечный продукт, поступающий непосредственно потребителю. x_ij – количество продукции i-ого вида, потребляемой для изготовления j-ой продукции в количестве X_j; Y_i – выпуск конечной продукции i-ого вида. Потребность в производстве продукции i-ого вида (валовый выпуск) равен сумме промежуточного и конечного продукта: 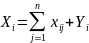. a_ij – норма расхода продукции i-ого вида на производство продукции j-ого вида (a_ij = x_ij / x_j) – коэффициент прямых затрат. 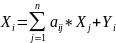=> или в матричной форме X = AX + Y. из этого балансового уравнения можно найти: 1. Валовый выпуск продукции путем умножения матрицы коэффициентов полных затрат на вектор конечной продукции: X = (E – A)^-1*Y. 2. Распределения продукции между цехами путем умножения коэффициентов прямых затрат на валовый выпуск: x_ij = a_ij*x_j.