98.Прямокутна система координат на площині
99.Полярні координати. Залежність між прямокутними і полярними координатами.
100.Рівняння лінії на площині. Рівняння прямої з кутовим коефіцієнтом.
Кутовий коефіцієнт у рівнянні прямої
Якщо
рівняння прямої можна записати у
вигляді
,
то коефіцієнт
k називається
кутовим
коефіцієнтом прямої.
1.
Дві прямі паралельні тоді й тільки тоді,
коли у них збігаються кутові коефіцієнти,
а точки перетину з віссю ординат різні.
2.
Кутовий коефіцієнт з точністю до знака
дорівнює тангенсу гострого кута,
утвореного прямою з віссю абсцис (або
дорівнює тангенсу кута між прямою й
додатним напрямком осі Ox).
3.
Прямі, що задані рівняннями
і
,
перпендикулярні тоді й тільки тоді,
коли
.
101. Рівняння прямої, що проходить через дві задані незбіжні точки
Рівняння прямої,
що проходить через дві задані незбіжні
точки
і
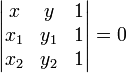
або
або в загальному вигляді
102.Означення і рівняння кола
103.Означення еліпса. Канонічне рівняння еліпса.
104.Означення гіперболи. Канонічне рівняння гіперболи.
105.Властивості дослідження форми гіперболи. Ексентриситет, директриси гіперболи.
106.Означення рівняння параболи. Дослідження флрми параболи.
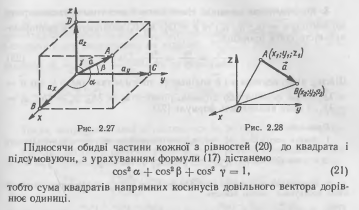
107.Прямокутна система координат у просторі. Означення вектора. Колінеарність векторів.
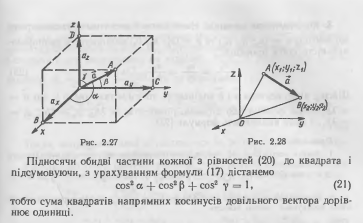
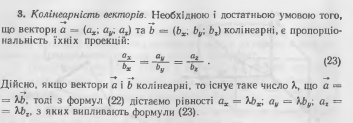
108.Проекція вектора на осі координат. Напрямні косинуси вектора.
109.Лінійні операції над векторами. Властивості лінійних операції.
110.Означення та основні властивості скалярного добутку.
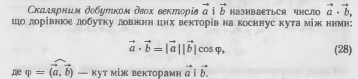
111.Рівняння площини, що проходить через 3 точки. Рівняння площини у відрізках на осях.
112.Загальне рівняння прямої в просторі.
113.Канонічне рівняння прямої у просторі
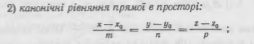
114.Кут між двома прямими у просторі. Умови паралельності і перпендикулярності двох прямих.
115.Відстань від точки до прямої в просторі
116.Взаємне розташування прямої і площини
117.Формула трапеції
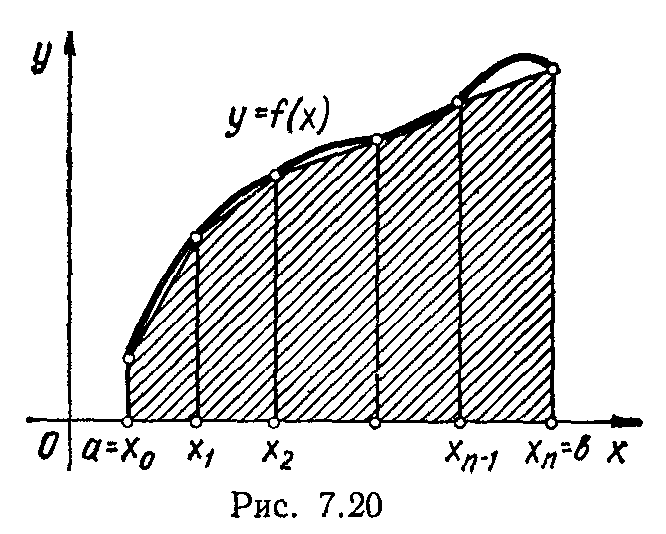
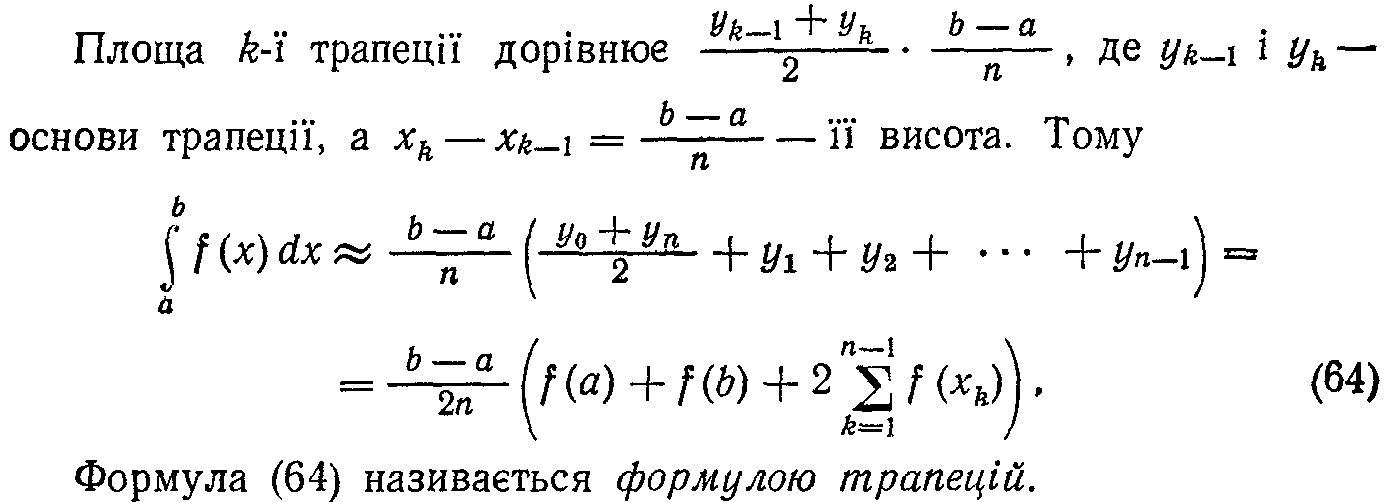
118.Обчислення площ плоских фігур
119.Поняття невласного інтегралу. Невласний інтеграл І роду
120 . Невласні інтеграли ІІ роду.
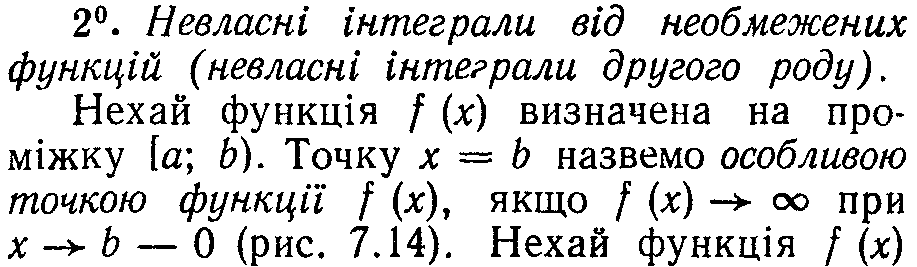
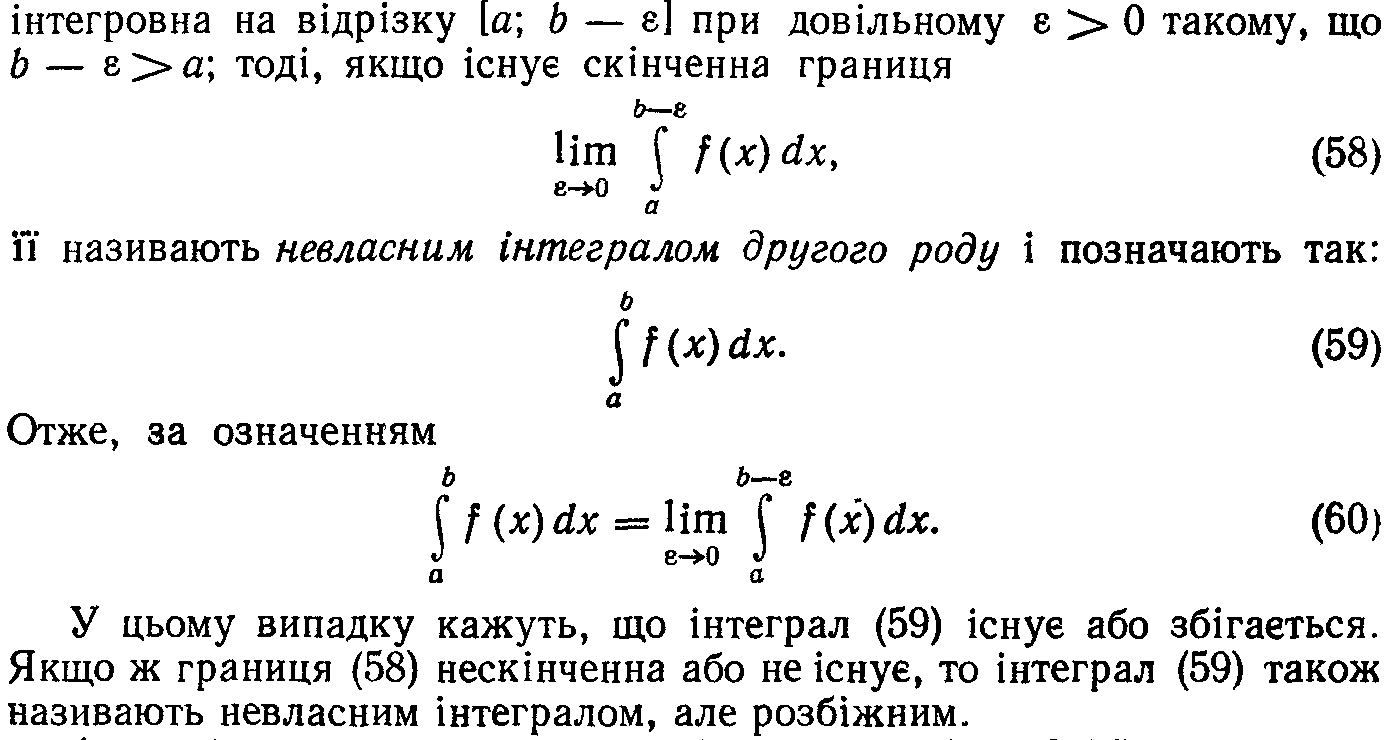
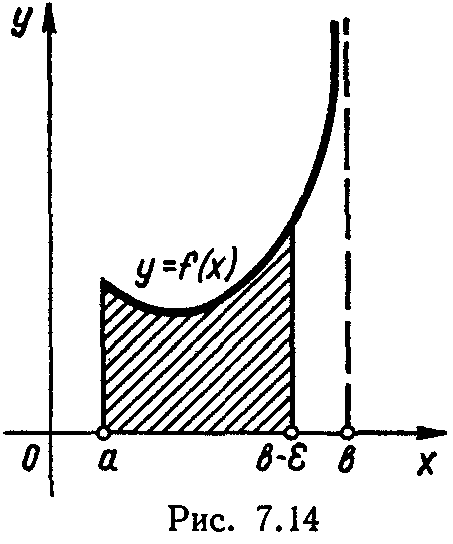
121. Теорема про збіжність інтегралів І роду
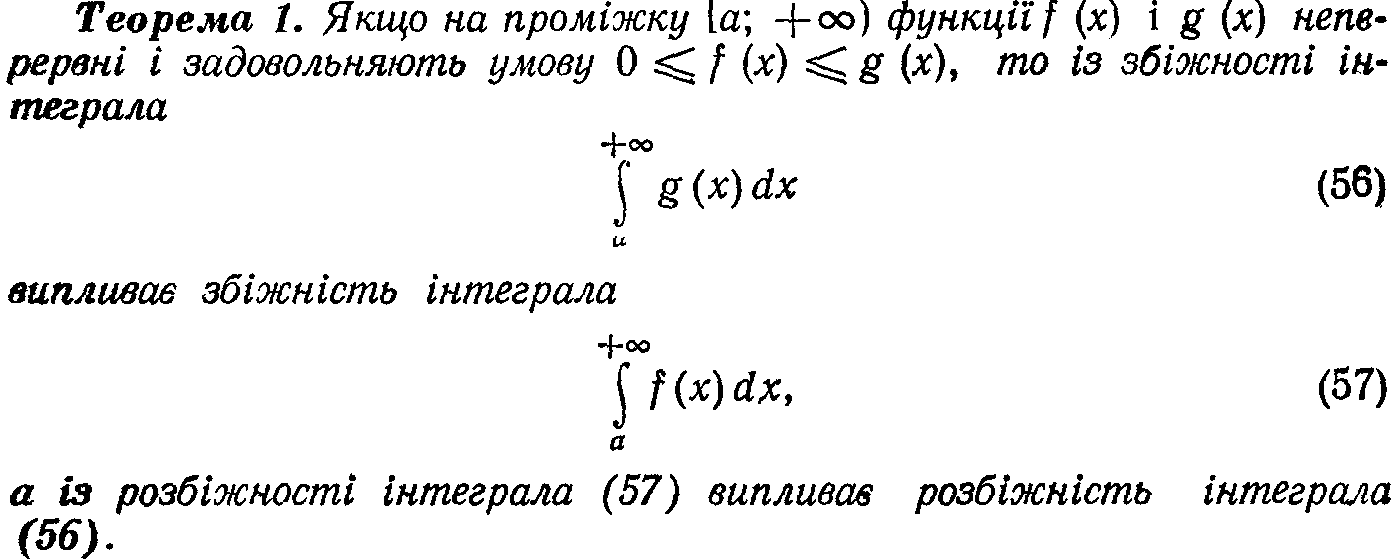
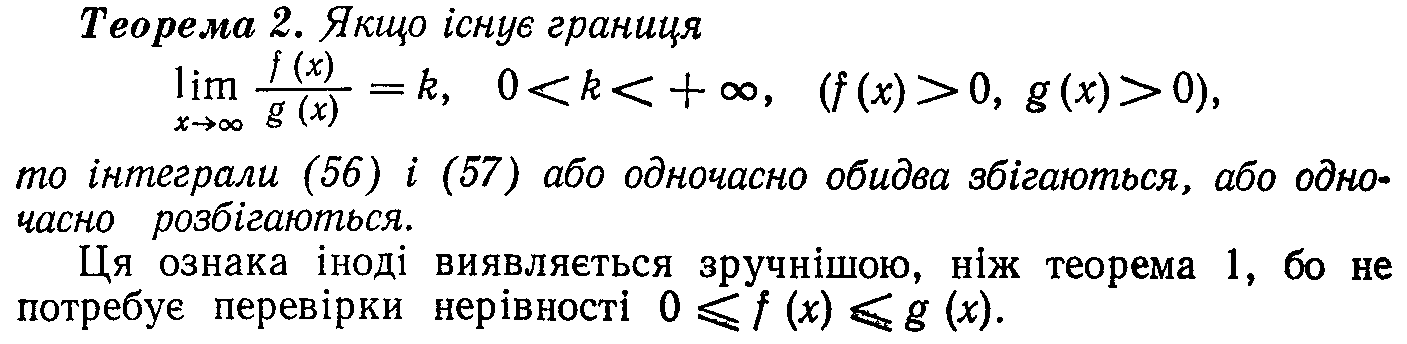
122.Теорема про збіжність невласних інтегралів ІІ роду
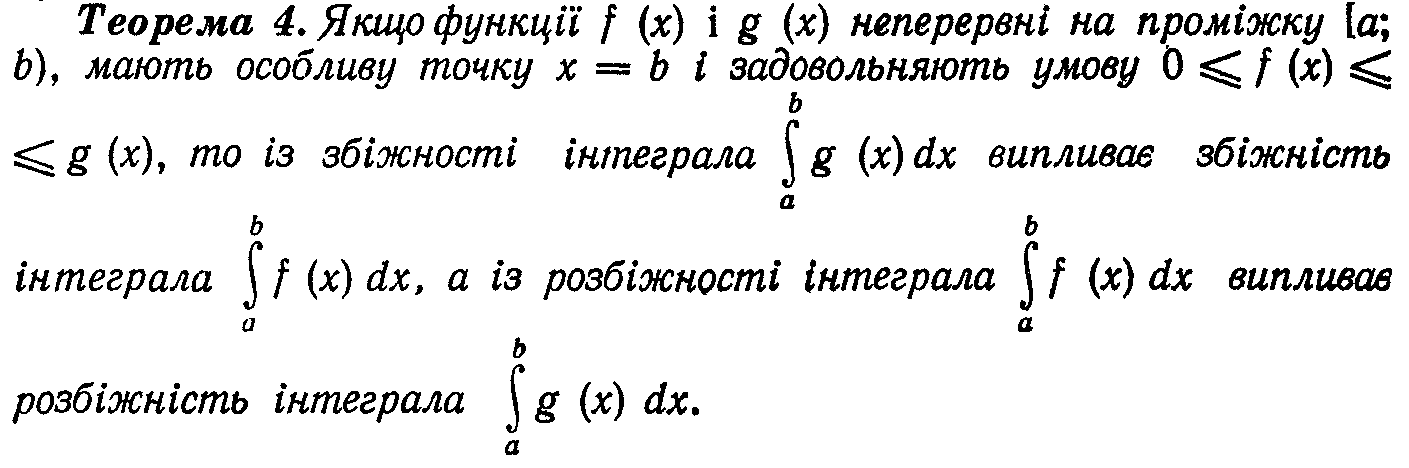
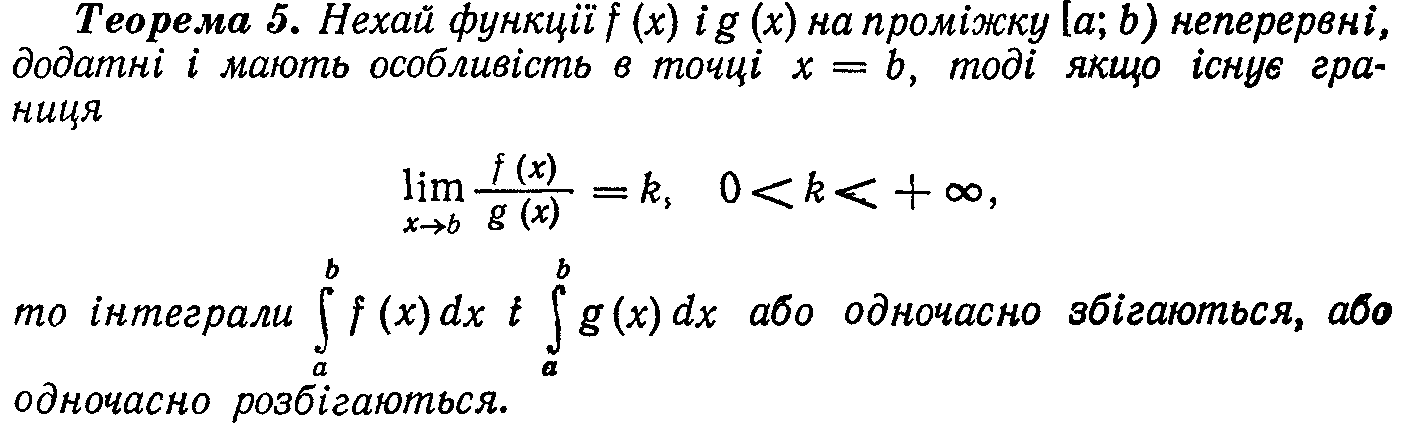
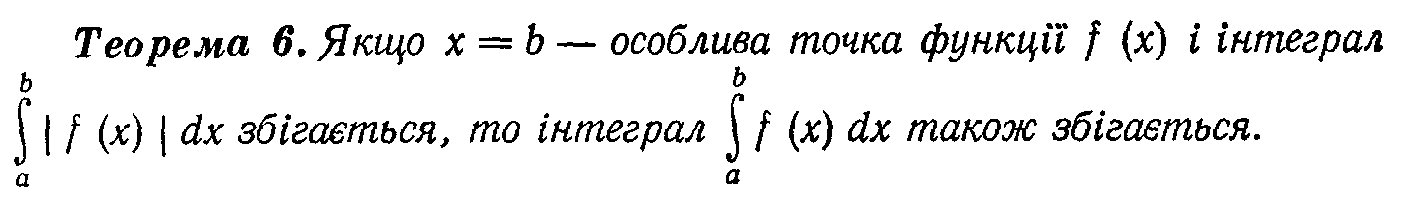
123.Диференціальні рівняння першого порядку…
124.
125.
126.
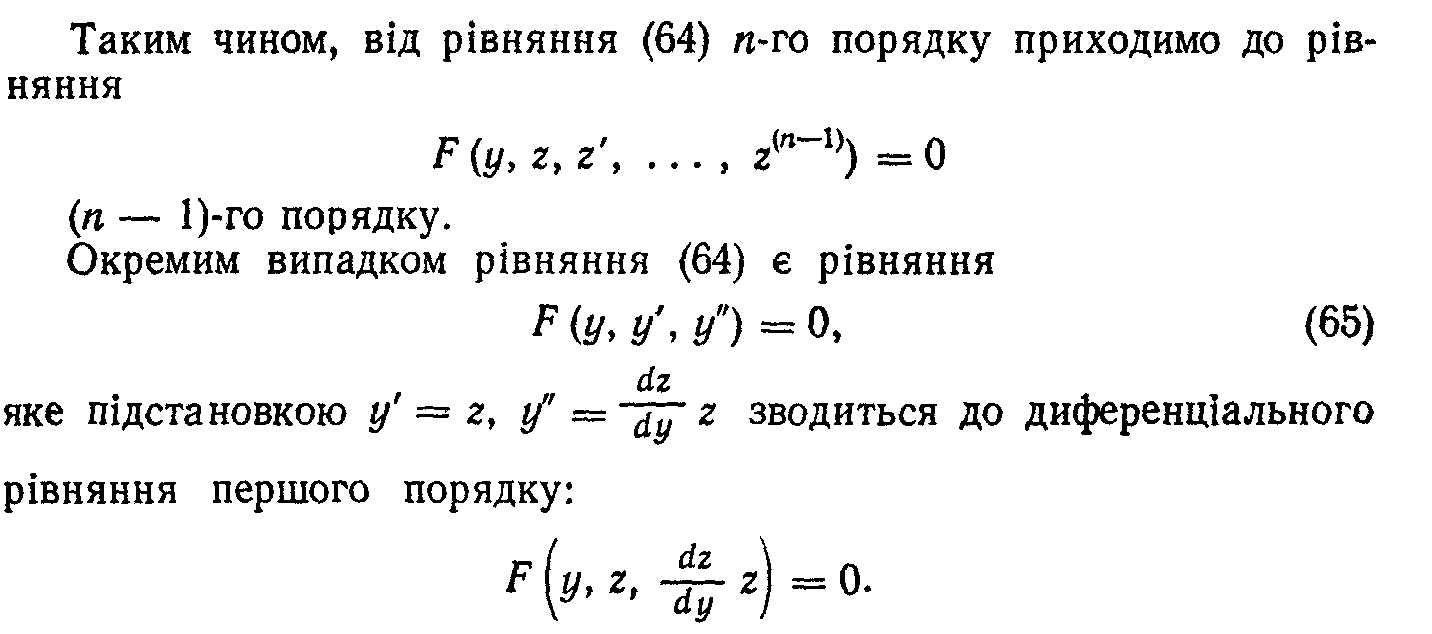
127.
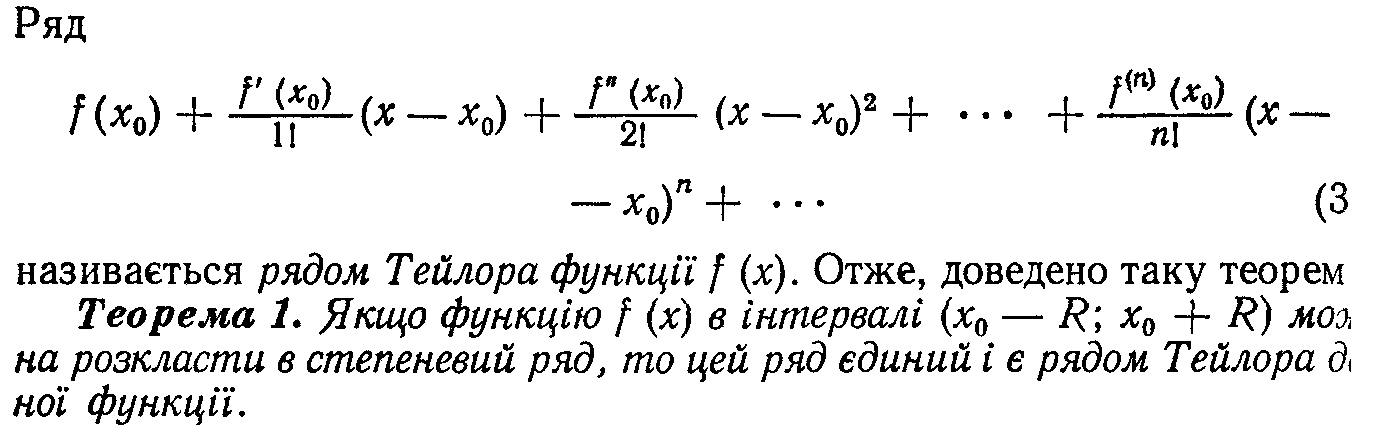
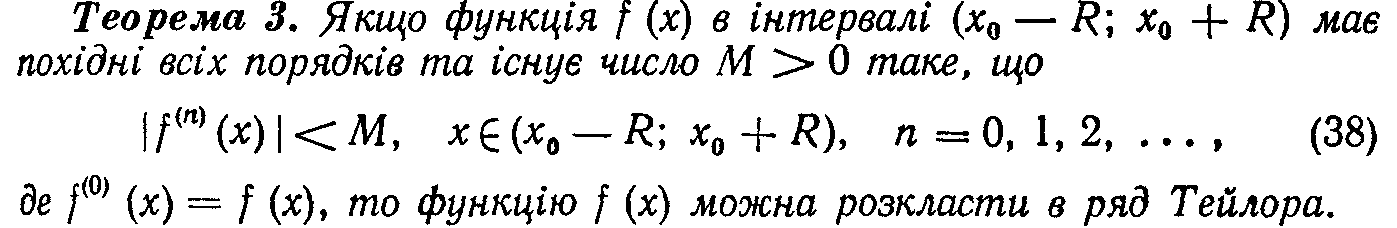
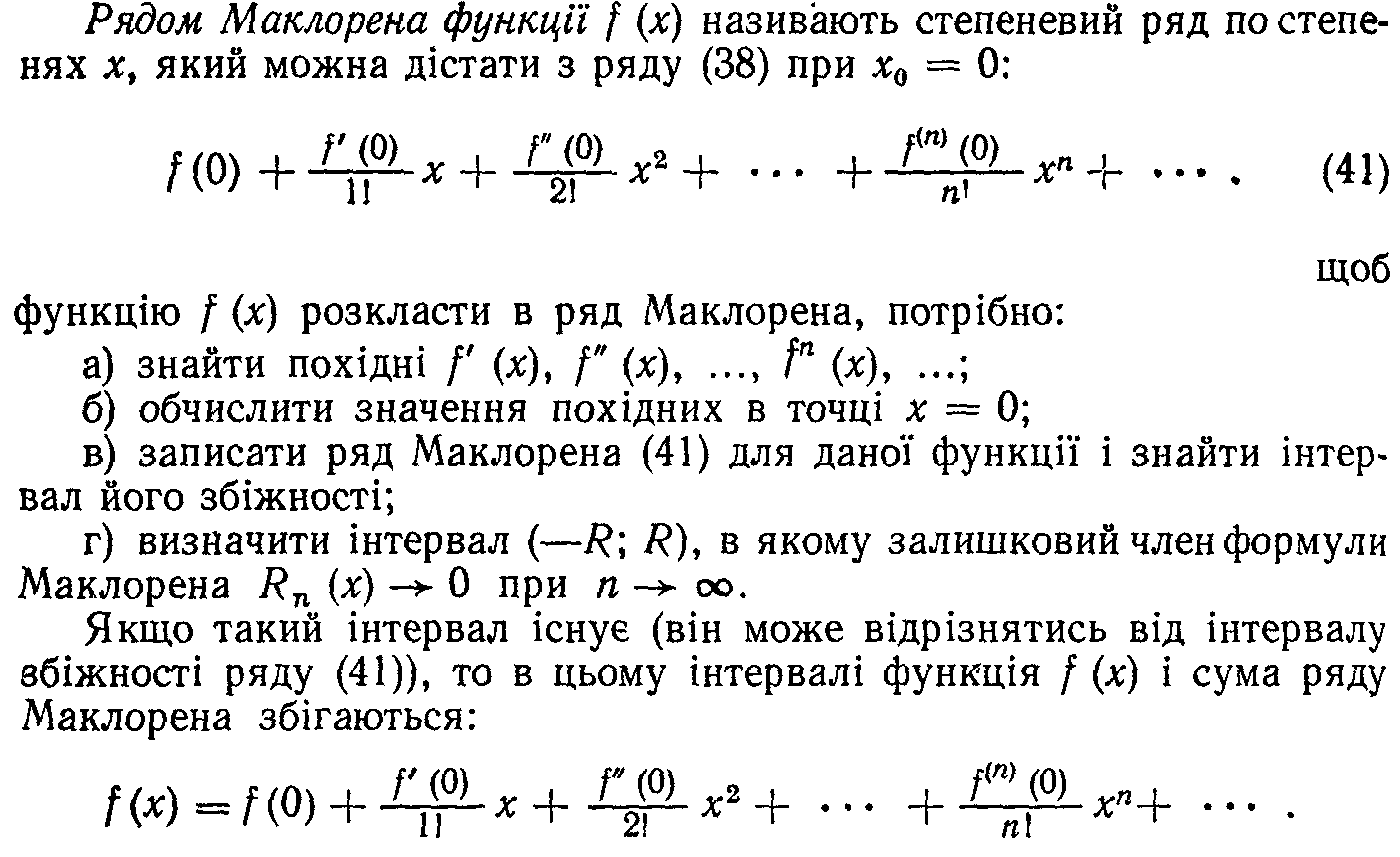
128.
129.Поняття еластичності попиту
