90. Загальне рівняння прямої

Рівняння вигляду Ах+Ву+С=0 називається загальним рівнянням прямої на площині.

Дослідження рівняння:

1)А не дорівнює 0, В не дорівнює 0, С не дорівнює 0, тоді з рівняння можна отриматити рівняння прямої у відрізку на осях:х/а+у/в=1, а=-С/А, в=-С/В

2)А = 0,Ву+С=0

Пряма паралельна осі Ох.

3)В=0, Ах+С=о

Пряма паралельна осі Оу

4)С=0, Ах+Ву=0

Пряма проходитьь через початок координат

5)А=С=0,Ву=0, вісь Ох

6)В=С=0, Ах=0,вісь Оу

8.Використоємо рівняння прямої з кутовим коефіцієнтом(у-у0=к(х-х0)), враховуючи, що точки М1(х1;у2) і М2(х2;у2) лежать на цій прямій, тоді маємо систему

у-у1=к(х-х1)

у2-у1=к(х2-х1),

Тоді точки М1 і М2 задовольняють рівняння у-у0=к(х-х0).

Виключаючи з цієї точки системи коефіцієнт к,отримуємо:

у-у1/у2-у1=х-х1/х2-х1 - рівняння прямої, яка проходить через дві задані точки

91. Відстань між двома точками на площині

Віддаль між двома точками — довжина уявного відрізка, кінцями якого є ці точки. Найкоротший шлях, яким можна дістатися з однієї точки в іншу.

Знайдемо відстань d між точками M₁ і M₂.

Згідно з теоремою Піфагора

Якщо позначити різницю як , а як , то формула набуває такого вигляду:

92. Поділ відрізків у заданому відношенні

Поділ відрізка у заданому відношенні - кажуть, що точка поділяє відрізок у відношенні , якщо виконано співвідношення .

Нехай на площині задано дві точки. Необхідно знайти точку , що лежить на відрізку і ділить його у відношенні .

З елементарної геометрії можна записати, що , тоді , і звідси знайдемо ; .

Якщо , то ; і точка M ділить відрізок навпіл.

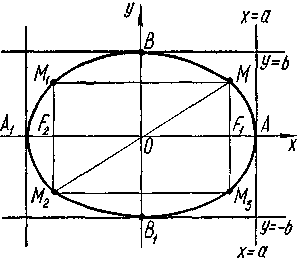
93.Властивості дослідження форми еліпса. Екцентриситет, директриси еліпса. Фокальні радіуси точки.

Еліпс в геометрії — лінія другого порядку.

Геометричне визначення

Е ліпсом називається множина всіх точок площини, для кожної з яких сума відстаней до двох даних точок F1 іF2 цієї площини є величина стала, більша за відстань між F1 іF2 .

Х^2/a^2+y^2/b^2=1 (1).канонічне рівняння еліпса.оскільки 2а>2c a^2-c^2=b^2.Оскільки рівняння(1) містить тільки члени з парними степеннями х і у, то еліпс симетричний відносно осей Ох і Оу, а також початку координат.точка О з координатами(0;0) називається центром еліпсаЕліпс перетинає осі координат в точак А1(-а; 0),В1(0;в), А2(а;0),В2(0;-в)т—ці точки називаються вершинами еліпса.А1А2=2а, В1В2 = 2в називаються великою і салою осями еліпса,відповідно а,в, називаються великою і малою півосями еліпса.

Директриса та ексцентриситет

Число e =Ве c/a - це ексцентриситет еліпса, величина, що характеризує його витягнутість; для еліпсу <1. Прямі, рівняння яких x = - a/e і x = a/e називаються директрисами еліпса; співвідношення відстані від будь-якої точки еліпса до найближчого фокусу до відстані до найближчої директриси стале і дорівнює ексцентриситету.F1(-с;0) і F2(с;0) – фокуси еліпса.F1F2 – фокальна відстань.З ауважимо, що величинами, які характеризують еліпс, є велика і мала півосі a і b, відстань c фокуса від центру, ексцентриситет e . Залежність між ними виражається формулами: . Тому, щоб скласти рівняння еліпса, досить знати або півосі a і b, або одну піввісь і ексцентриситет і т.д.Я кщо точки F1 і F2 збігаються, то еліпс стає колом радіуса a . При цьому .Отже, коло є окремим випадком еліпса.

Визначальна властивість еліпса:

Т очки F1 іF2 називають фокусами еліпса, а відстань між ними — фокальна відстань, її позначають через 2c , отже

С уму відстаней від будь-якої точки M еліпса до фокусів F1 і F2 позначимо 2a . Тоді за означенням маємо: .

Звідси можна сказати, що еліпс складається з таких і тільки таких точок M, які задовольняють умові:

Весь еліпс вміщується впрямокутник зі сторонами 2а і 2в,сторони прямокутника дотикаються до еліпса в його вершинах.Якщо а=в, то рівняння(1) набирає вигляду х^2+e^2=a^2? а це коло.Коло-це еліпс, у якого фокуси збігаються з його центром.Міра відхилення еліпса від кола характеризується величиною Епсілон(Е),яка називається ексцентриситетом еліпса і дорівнює Е=с\а(визначає форму еліпса).Якщо Е=0,то в.=а і еліпс перетворюється в коло.Якщо Е наближається до1 то відношення в\а зменшується,тобто еліпс все більше розтягується взовдж осі Ох.Нехай М з координатами(х;у) – довільна точка еліпса з фокусами F1 і F2 відстані F1M іF2M,які називаються фокальними радіусами точки М. F1M=r1 іF2M=r2.r1+r2=2a.Прямі х=+-а\Е називаються директрисами еліпса.відношення фокальних радіусів довільної точки еліпса до відстаней цієї точки від відповідних дтректрис є величина стала і дорівнює ексцентриситету еліпса.r1\d1=r2\d2=E

94.Означення матриці. Ранг матриці.

Матрицю називатимемо матрицею східчастого виду, якщо вона задовольняє слідуючим умовам: 1. якщо i-тий рядок складений з нулів, то (i+1)-ший рядок також складений з нулів;

2.  якщо перші ненульові елементи i-го та (i+1)-го рядків розташовано в стовпцях з номерами ki та ki+1, відповідно, то ki ki+1.

Усяку матрицю скінченим числом елементарних перетворень рядків можна звести до східчастого виду.

Кажуть, що матриця A еквівалентна матриці B , якщо B одержана з A за декілька елементарних перетворень.

Через Est будемо позначати квадратну матрицю, в якій на перетині s-го рядка та t-го стовпця стоїть 1, а всі інші елементи - нульові. Такі матриці називатимемо матричними одиницями.

Елементарними матриці, які одержано з одиничної матриці за допомогою одного з елементарних перетворень.

Fst=E−Ess−Ett+Est+Ets

Fs( )=E+( −1)Ess

Fst( )=E+ Est

де s =t =0.

Елементарні матриці неособливі, причому

(Fst)−1=Fst;(Fs( ))−1=Fs( −1);(Fst( ))−1=Fst(− )

Множення матриці A на а) матрицю Fst зліва (справа) рівносильно переставленню s-го та t-го рядків (стовпців) матриці A;

б) матрицю Fs( ) зліва (справа) рівносильно множенню s-го рядка (стовпця) матриці A на число ;

в) матрицю Fst( ) зліва (справа) рівносильно додаванню до s-го рядка t-го рядка (до t-го стовпця - s-го стовпця) матриці A, помноженного на число .

Усяку матрицю A за допомогою деяких матриць S і T (тобто, за допомогою елементарних перетворень рядків і стовпців) можна привести до виду

SAT= Er 0 0 0    

де r - порядок одиничної матриці.

Мінором k-го порядку матриці A називатимемо детермінант підматриці, утвореної з елементів матриці A, які стоять на перетині вибраних k рядків та k стовпців, і розміщених в тому самому порядку, що і в матриці A. Рангом матриці називається найвищий порядок відмінних від нуля мінорів цієї матриці. Ранг матриці A позначають rangA або r(A). Елементарні перетворення матриці не змінюють її ранга. Ранг східчастої матриці дорівнює числу її ненульових рядків.