ЛАБОРАТОРНА РОБОТА №1

ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ

1.1. Мета лабораторної роботи

Здобуття практичних навичок у побудові інтерполяційних багаточленів Лагранжа і Ньютона та використанні їх для обчислення наближених значень функцій поза вузлами інтерполяції.

1.2. Основні відомості

1.2.1. Постановка задачі

Для функцій, заданих таблицями їхніх значень на кінцевому інтервалі, виникає необхідність обчислення значень функцій для значень аргументів, відсутніх у таблиці. Тоді будують функцію, що у заданих точках приймає задані значення, а в інших точках інтервалу приблизно представляє задану функцію. А потім обчислення значень функції для будь-яких значень аргументу в області визначення таблично заданої функції виконують за побудованою функцією. Задача інтерполяції – побудова такої наближеної функції. Найчастіше інтерполяційну функцію знаходять у вигляді алгебраїчного багаточлену. Геометрично задача інтерполяції полягає в побудові кривої y=F(x), що проходить через таблично задану систему точок M₀(x₀,y₀), M₁(x₁,y₁), …, M_n(x_n,y_n).

1.2.2. Інтерполяційна формула Лагранжа

Нехай функція y=f(х) у точках x₀, x₁, ..., x_n відповідно приймає значення y₀, y₁, ..., y_n. Потрібно побудувати багаточлен L_n(x) ступеня не вище n, що приймає в точках x₀, x₁, ..., x_n (вузлах інтерполяції) значення y₀, y₁, ..., y_n. Відстань між вузлами інтерполяції може бути різною. Розв'язок цієї задачі – багаточлен Лагранжа

.(1.1)

Інтерполяційну формулу Лагранжа можна записати в більш стислому вигляді:

, (1.2)

де – так звані базисні функції, чисельник яких містить всі різниці (x–x_k), а знаменник – всі різниці за винятком (x_k–x_k).

При цьому в точках x₀, x₁, …, x_n значення багаточлену L_n(x) та функції f(x) збігаються. При інших значеннях x різниця в загальному випадку відмінна від нуля і являє собою істинну похибку методу. Величина R_n(х) є залишковим членом інтерполяції.

Приклад 1.1. Задана функція

x	1,1	1,5	2,0	2,6
y	0 ,0953	0,4055	0,6931	0,9555

Побудувати інтерполяційний багаточлен Лагранжа й обчислити наближене значення функції для x=1,3.

Розв'язок.

Для побудови інтерполяційного багаточлену скористаємося формулою (1.1) при n=3:

Перевіряємо значення функції для вузлів інтерполяції:

L₃(1,1) = 0,06481,1³ – 0,52071,1² + 1,79811,1 – 1,3389 ≈ 0,0953;

L₃(1,5) = 0,06481,5³ – 0,52071,5² + 1,79811,5 – 1,3389 ≈ 0,4055;

L₃(2,0) = 0,06482³ – 0,52072² + 1,79812 – 1,3389 ≈ 0,6931;

L₃(2,6)= 0,06482,6³ – 0,52072,6² + 1,79812,6 – 1,3389 ≈ 0,9555.

Обчислюємо f(1,3)  L₃(1,3)  0,2611.

Відповідь: f(1,3) = 0,2611.

Інтерполяційну формулу в Excel можна побудувати досить простим способом. З практичної точки зору головна проблема полягає в обчисленні в довільній точці значень базисних функцій. Як приклад розглянемо задачу про побудову інтерполяційного полінома Лагранжа за даними Прикладу 1.1.

Н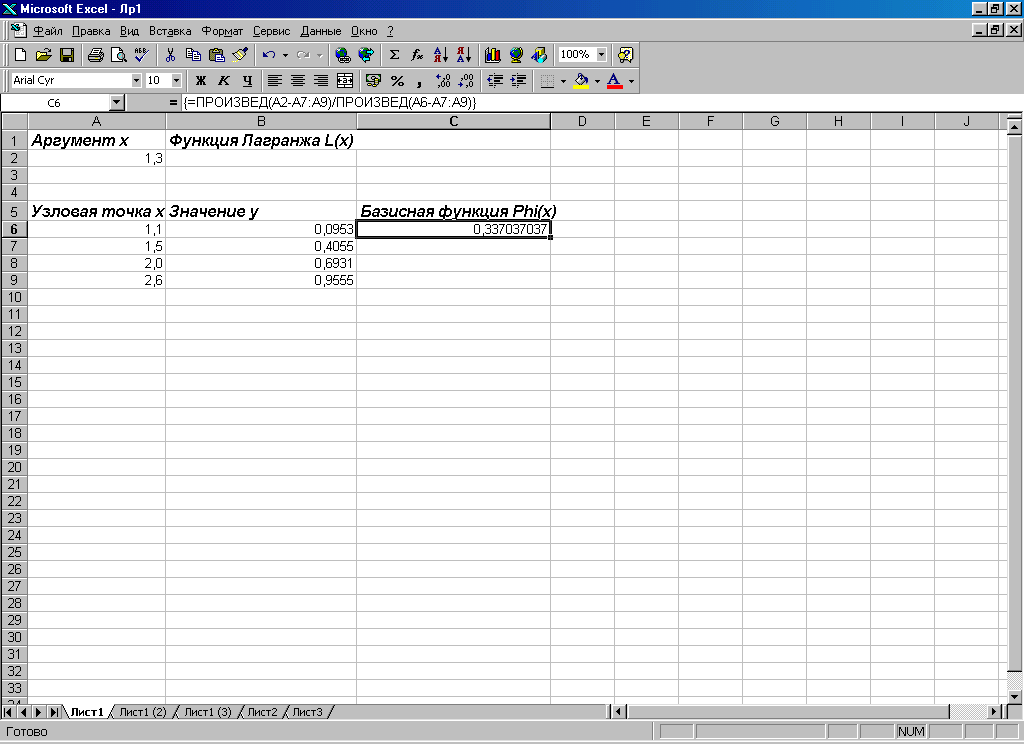 а рис. 1.1 представлені вихідні дані, за якими буде виконуватися інтерполяція. На цьому ж рисунку проілюстрований процес визначення першої базисної функції.

Рис.1.1

У діапазоні комірок А6:А9 представлені задані значення аргументів функції, а в діапазоні комірок В6:В9 – значення функції для вузлових точок аргументу. В комірку А2 вводиться значення аргументу, для якого необхідно обчислити значення інтерполяційного полінома. Значення полінома буде виводитися в комірку В2. Важливим моментом є заповнення комірок у діапазоні С6:С9, де будуть відображатися значення базисних функцій у точці, що зазначена в комірці А2. Саме за цими значеннями і значенням комірок з діапазону А6:А9 визначається значення інтерполяційного полінома (комірка В2).

Діапазон С6:С9 заповнюється так: окремо перша і остання комірки діапазону, а всі інші комірки – поширенням однієї формули. Зокрема, в комірку С6 вводиться формула =ПРОИЗВЕД(A2-A7:A9)/ПРОИЗВЕД(A6-A7:A9), відповідно до якої визначається перша базисна функція. Відразу слід зазначити, що й ця формула, і всі інші формули з діапазону С6:С9, вводяться як формули для діапазонів, тобто за допомогою натискання комбінації клавіш Ctrl+Shift+Enter. Причина полягає в тому, що аргументами функції ПРОИЗВЕД() вказуються результати арифметичних операцій з діапазонами.

Далі заповнюються комірки з діапазону С7:С8. Для цього в комірку С7 вводиться формула =ПРОИЗВЕД($A$2-$A$6:A6;$A$2-A8:$A$9)/ ПРОИЗВЕД(A7-$A$6:A6;A7-A8:$A$9). Абсолютні й відносні посилання у формулі підібрані так, щоб при її копіюванні в наступні комірки, посилання на початкову С6 і кінцеву С9 комірки діапазону, так само як і на комірку А2 зі значенням змінної, для якої обчислюється базисна функція (і весь поліном), залишалися незмінними. Це абсолютні посилання. Разом з тим, в процесі копіювання формули добутку в ній обчислюються без урахування значення аргументу в тому рядку, де розміщена формула. Після введення формули в комірку С7 дана формула за допомогою маркеру заповнення копіюється в усі комірки, аж до С8.

Н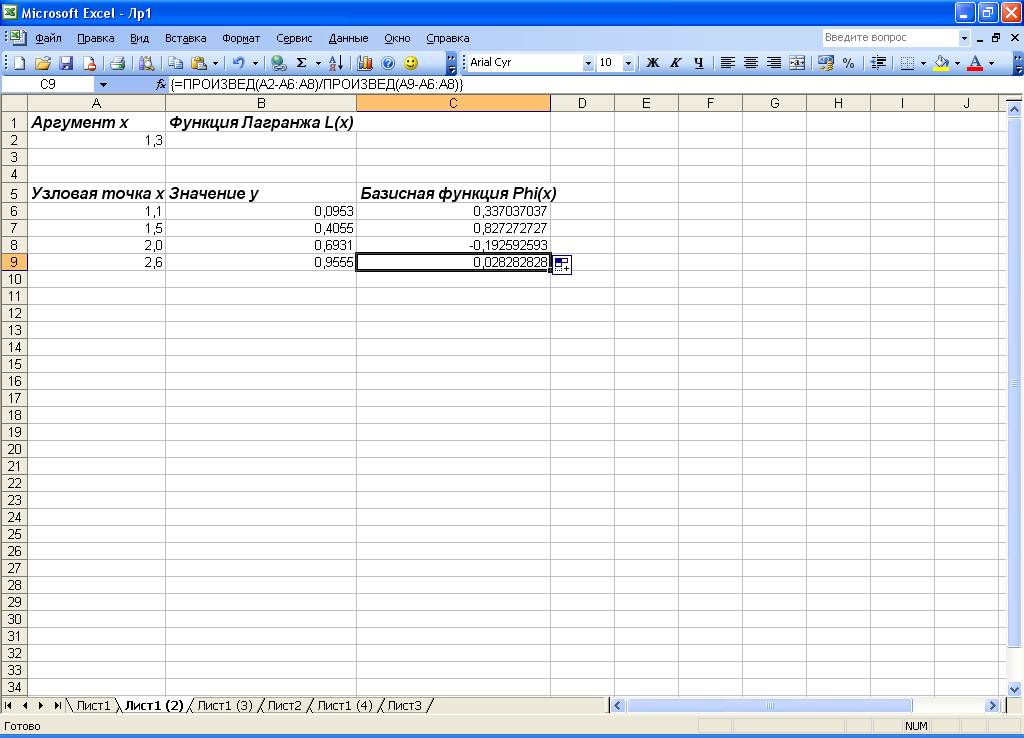 арешті, в комірку С9 необхідно ввести формулу =ПРОИЗВЕД(А2-А6:А8)/ ПРОИЗВЕД(А9-А6:А8). Оскільки формули з початкової С6 і кінцевої С9 комірок діапазону С6:С9 нікуди копіювати не передбачається, то й посилання там відносні. Результат можна бачити на рис. 1.2.

Рис. 1.2

Після цього залишилося обчислити значення інтерполяційного полінома. Для цього досить в комірку В2 ввести формулу =СУММПРОИЗВ(B6:B9;C6:C9). Ця формула вводиться як звичайна, тобто потрібно натиснути клавішу Enter. Результат представлений на рис. 1.3.

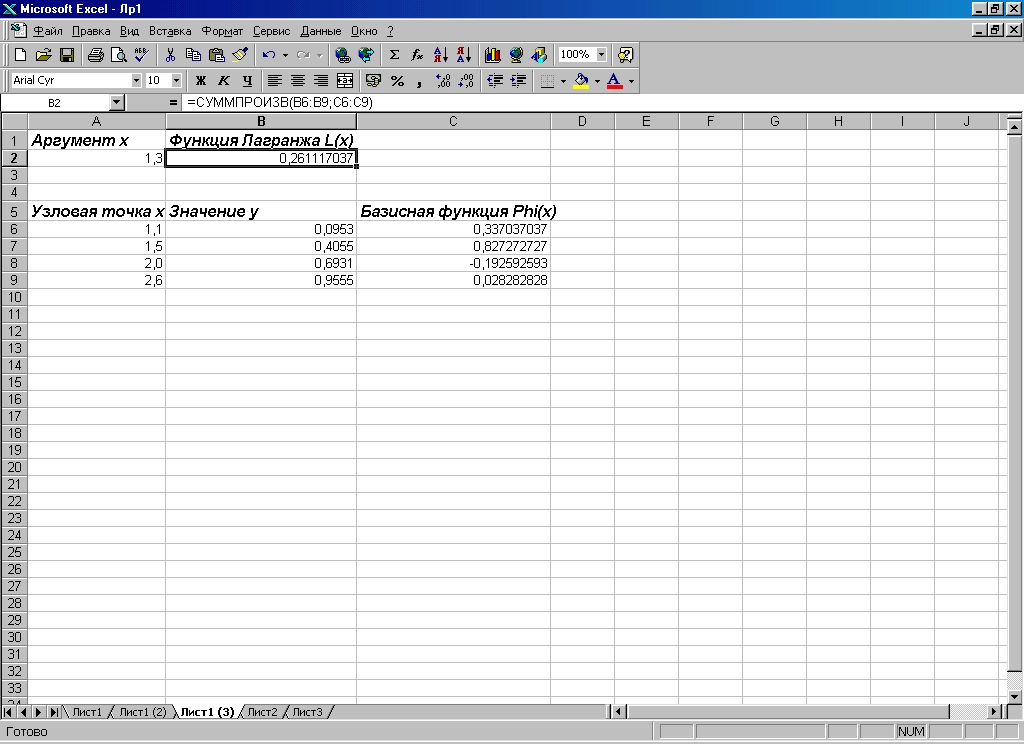
Рис.1.3

Для розрахунку значення полінома в якійсь точці, відповідне значення варто ввести в комірку А2. В комірці В2 практично відразу з'явиться результат.

Відповідь: f(1,3) = 0,2611.

Н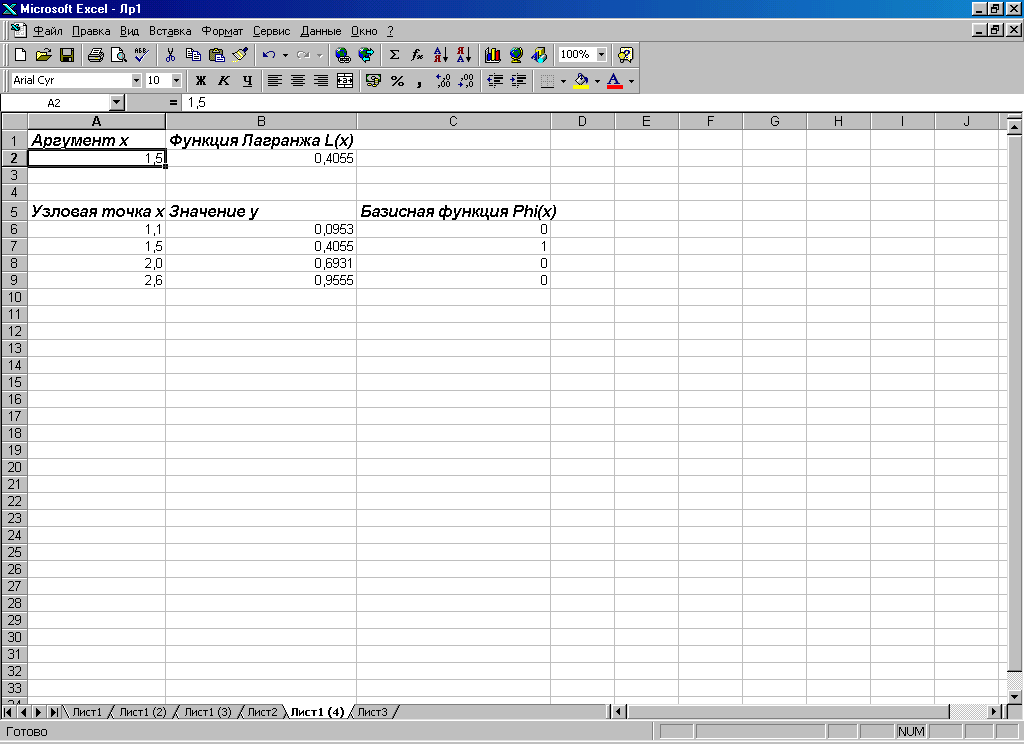 а рис. 1.4 проілюстрована ситуація, коли в якості аргументу зазначене вузлове значення. Як і слід було сподіватися, у вузловій точці значення інтерполяційного полінома дорівнює експериментальному значенню функції в цій точці, а всі базисні функції, крім тієї, що відповідає зазначеному вузлу, дорівнюють нулю. Відмінна від нуля базисна функція дорівнює одиниці.

Рис.1.4

Використання Excel для розв'язання задач цього класу є досить ефективним і розкриває широкі обрії перед кожним дослідником.

Запропонований спосіб побудови інтерполяційного полінома, безумовно, не єдиний. Крім того, поліном зовсім не обов'язково знаходити саме у формі Лагранжа. Тому вибір методу, типу інтерполяційного полінома і вирішення інших подібних питань здійснюється, як правило, у контексті конкретної задачі.