4. Модифицированный метод Ньютона
Рассмотренный выше метод Ньютона требует вычисления производной на каждом шаге. В некоторых случаях это может существенно снизить эффективность метода (в смысле затрат машинного времени). Поэтому в тех случаях, когда вычисление производной сопряжено с существенными затратами машинного времени, используют модифицированный метод Ньютона, в котором производная вычисляется только в точке начального приближения :
.
(2.19)
5. Метод секущих
Еще одна модификация метода Ньютона
связана с приближенным вычисление
производной
в окрестности точки
по формуле
.
Подставляя это выражение в формулу Ньютона (2.15), приходим к формуле
,
,
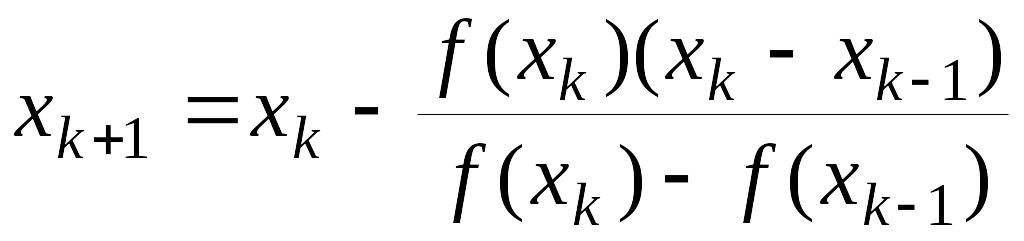(2.20)
которая определяет метод секущих.
Название метода связано с его геометрической
интерпретацией (см. рис. 2.10). Секущая,
проведенная через точки
и
,
пересекает ось абсцисс в точке
,
значение которой определяется формулой
(2.20).
Д
ля
того, чтобы начать итерационный процесс
в методе секущих необходимо задать два
начальных приближения: нулевое
и первое
.
На практике, как правило, поступают
следующим образом: нулевое приближение
выбирают аналогично выбору начального
приближения в методе Ньютона, а в качестве
первого приближения выбирают величину
,
где e – заданная
погрешность. Эти значения используются
для нахождения последующего (второго)
приближения
по формуле (2.20). Затем, значения
и
используют для определения третьего
приближения
и т.д. Альтернативно, в качестве нулевого
и первого приближений могут быть выбраны
границы отрезка локализации корня, если
они известны. В этом случае первая
итерация метода секущий даст результат,
аналогичный методу хорд. Для завершения
итерационного процесса можно
воспользоваться условием (2.14).
Метод секущих несколько уступает методу Ньютона в скорости сходимости, однако он не требует вычисления производной и поэтому оказывается особенно полезным в тех случаях, когда получение аналитического выражения для производной затруднено или невозможно, например, если функции получена в ходе численных расчетов, а не задана аналитически.
По алгоритму метод секущих близок к методу хорд, однако в отличие от последнего начальные приближения в методе секущих могут располагаться как с разных сторон от корня, так и с одной стороны; кроме того при уточнении корня не проверяются знаки функции .
6. Метод простых итераций
Теперь рассмотрим более общий итерационный метод уточнения корней. Представим исходное уравнение в виде
.
(2.21)
О том как преобразовать исходное уравнение к виду (2.21) буден рассказано ниже.
Пусть нам известно начальное приближение
к корню
(
).
Подставив его в правую часть уравнения
(2.21) получим новое приближение
,
затем аналогичным образом получим
и так далее,
,
.
(2.22)
Оказывается, что при определенных
свойствах функции
последовательность
,
определяемая по формуле (2.22), сходится
к корню уравнения
.
Необходимо установить при каких условиях
итерационный процесс (2.22) будет сходящимся.
Приложение 2