Пример возможного выполнения раздела «Анализ, формальная постановка и выбор метода решения»

( http://physics.herzen.spb.ru/library/01/01/nm_labs/nonlineareq.htm )

Численное решение нелинейных уравнений

1. Понятия и определения

1. Постановка задачи. Решение нелинейных уравнений с одним неизвестным является одной из важных математических задач, возникающих в различных разделах физики, химии, биологии и других областях науки и техники.

В общем случае нелинейное уравнение с одним неизвестным можно записать в виде:

, (2.1)

где – некоторая непрерывная функция аргумента x.

Всякое число , обращающее функцию в нуль, т.е. при котором , называется корнем уравнения (2.1). Если в точке наряду с функцией обращаются в ноль и ее производные до порядка включительно, то число называют корнем k-й кратности. Однократный корень также называют простым. В дальнейшем мы будем говорить именно о простых корнях.

В зависимости от вида функции нелинейные уравнения подразделяются на два класса – алгебраические и трансцендентные^1[1].

Уравнение (2.1) называется алгебраическим, если функция является алгебраической функцией. Алгебраическое уравнение всегда может быть представлено в канонической форме:

, (2.2)

где – коэффициенты уравнения. Показатель n называют степенью алгебраического уравнения.

Если функция содержит тригонометрические, показательные, логарифмические и другие функции, не являющиеся алгебраическими, то уравнение (2.1) называется трансцендентным. Примерами трансцендентных уравнений являются:

.

Методы решения нелинейных уравнений делятся на прямые (аналитические, точные) и итерационные. Прямые методы позволяют записать решение в виде некоторого соотношения (формулы). При этом значения корней могут быть вычислены по этой формуле за конечное число арифметических операций. Подобные методы развиты для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Однако подавляющее большинство нелинейных уравнений, встречающихся на практике, не удается решить прямыми методами. Даже для алгебраического уравнения выше четвертой степени не удается получить аналитического решения в виде формулы с конечным числом арифметических действий. Во всех таких случаях приходится обращаться к численным методам, позволяющим получить приближенные значения корней с любой заданной точностью^2[2].

При численном подходе задача о решении нелинейных уравнений разбивается на два этапа: локализация (отделение) корней, т.е. нахождение таких отрезков на оси x, в пределах которых содержится один единственный корень, и уточнение корней, т.е. вычисление приближенных значений корней с заданной точностью.

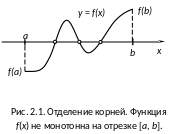
2. Локализация корней. Для отделения корней уравнения (2.1) необходимо иметь критерий, позволяющий убедится, что, во-первых, на рассматриваемом отрезке имеется корень, а, во-вторых, что этот корень единственный на указанном отрезке. Если функция непрерывна на отрезке , а на концах отрезка её значения имеют разные знаки , то на этом отрезке расположен, по крайней мере, один корень. Это условие (как видно из рисунка 2.1) не обеспечивает единственности корня. Достаточным дополнительным условием, обеспечивающем единственность корня на отрезке является требование монотонности функции на этом отрезке. В качестве признака монотонности функции можно воспользоваться условием знакопостоянства первой производной .

Таким образом, если на отрезке функция непрерывна и монотонна, а ее значения на концах отрезка имеют разные знаки, то на рассматриваемом отрезке существует один и только один корень. Заметим, что под этот критерий не подпадают кратные корни уравнений, например, очевидный корень уравнения .

Воспользовавшись этим критерием можно отделить корни аналитическим способом, находя интервалы монотонности функции.

Отделение корней можно выполнить графически, если удается построить график функции . В ряде случае бывает удобно заменить уравнение эквивалентным уравнением вида . Корни этого уравнения определяются абсциссами точек пересечения графиков функций и .

В качестве примера рассмотрим уравнение . Переходя к эквивалентному уравнению построим графики функций и (рис. 2.2)

И з графика видно, что уравнение содержит один корень, расположенный в интервале .

О тделение корней можно также выполнить табличным способом. Допустим, что все интересующие нас корни уравнения (2.1) находятся на отрезке . Выбор этого отрезка (интервала поиска корней) может быть сделан, например, на основе анализа конкретной физической или иной задачи. Будем вычислять значения , начиная с точки , двигаясь вправо с некоторым шагом h (рис. 2.3). Как только обнаруживается пара соседних значений , имеющих разные знаки, так соответствующие значения аргумента x можно считать границами отрезка, содержащего корень.

Надежность рассмотренного подхода к отделению корней уравнений зависит как от характера функции , так и от выбранной величины шага h. Действительно, если при достаточно малом значении h ( ) на границах текущего отрезка функция принимает значения одного знака, то естественно ожидать, что уравнение корней на этом отрезке не имеет. Однако, это не всегда так: при несоблюдении условия монотонности функции на отрезке могут оказаться корни уравнения (рис. 2.4а). Также несколько корней на отрезке могут оказаться и при выполнении условия (рис. 2.4б). П редвидя подобные ситуации, следует выбирать достаточно малые значения h.

Поскольку данный способ предполагает выполнение лишь элементарных арифметических и логических операций, количество которых может быть велико при малых значениях h, для его реализации целесообразно использовать вычислительные возможности компьютера.

Отделяя таким образом корни, мы, по сути, получаем их приближенные значения с точностью до выбранного шага. Так, например, если в качестве приближенного значения корня взять середину отрезка локализации, то абсолютная погрешность этого значения не будет превосходить половины шага поиска (h/2). Уменьшая шаг в окрестности каждого корня, можно, в принципе, повысить точность отделения корней до любого наперед заданного значения. Однако такой способ требует большого объема вычислений. Поэтому при проведении численных экспериментов с варьированием параметров задачи, когда приходится многократно осуществлять поиск корней, подобный метод не годится для уточнения корней и используется только для отделения (локализации) корней, т.е. определения начальных приближений к ним. Уточнение корней проводится с помощью других, более экономичных методов.

3. Уточнение корней. На данном этапе задача состоит в получении приближенного значения корня, принадлежащего отрезку , с заданной точностью (погрешностью) e. Это означает, что вычисленное значение корня должно отличаться от точного не более чем на величину e:

.

Процедура численного определения приближенных значений корней нелинейных уравнений, как правило, состоит в выборе начального приближения к корню и вычислении по некоторой формуле последующих приближений , и т.д. Каждый такой шаг называется итерацией (от латинского iteratio – повторение), а сами методы уточнения – итерационными методами. В результате итераций получается последовательность приближенных значений корня , которая называется итерационной последовательностью. Если эти значения с ростом k стремятся к точному значению корня :

, (2.3)

то говорят, что итерационный процесс сходится.

Сходимость итерационного процесса означает, что погрешность каждого последующего приближения должна быть меньше погрешности предыдущего приближения, т.е. погрешность приближенных значений с каждым шагом должна уменьшаться:

В общем случае это неравенство можно представить в виде:

, (2.4)

где и – некоторые числа, значения которых определяются методом уточнения корня. От значений q и a зависит насколько с каждым шагом уменьшается погрешность приближенных значений и, соответственно, насколько быстро можно получить приближенное значение с заданной точностью. Главным показателем скорости сходимости метода является значение a, называемое порядком сходимости. При погрешность с каждым шагом убывает линейно, в этом случае говорят о линейной сходимости. Если , то говорят, что имеет место сверхлинейная сходимость.