МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ГОРНЫЙ УНИВЕРСИТЕТ
Кафедра электротехники и информационных систем
Утверждаю
Зав. кафедрой ЭИС
проф., д.т.н.
______ С.З. Шкундин
«___» _____ 2007 г.
Лабораторная работа
«Использование уравнений Колмогорова для исследования систем массового обслуживания»
по дисциплине
«Проектирование информационных систем»
(4 часа)
Работу составил
Проф., к.т.н Максимов Н.А.
Москва, 2007
Цели работы.
Ознакомиться с методами использования Марковских систем для исследования СМО. Получить практические навыки в решении систем дифференциальных уравнений Колмогорова и их использовании для анализа систем массового обслуживания.
Порядок выполнения работы
Изучить теоретическую часть работы
Составить уравнения Колмогорова для заданного преподавателем варианта задания.
С помощью пакета MathCad провести необходимые расчеты и построить графики.
Проанализировать полученные графики и сделать выводы по работе
Оформить отчет и сдать зачет по работе.
Теоретическая часть Марковские случайные процессы
Пусть имеется физическая структура S, которая меняет свое состояние случайным образом, в этом случае говорят, что в системе протекает случайный процесс.
Случайный процесс, протекающий в системе, называется Марковским,
если для любого момента времени, вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент времени и не зависят от того, как и когда система пришла в это состояние.
Марковские процессы делятся на несколько классов:
Марковские процессы с непрерывным временем и непрерывным множеством состояний.
Процессы с дискретным временем и непрерывным множеством состояний.
Процессы с непрерывным временем и дискретным множеством состояний.
Процессы с дискретным временем и дискретным множеством состояний.
Множество состояний: S0,S1,S2,S3.
Уравнение Колмогорова для вероятностей состояний
Некоторые системы описываются в виде графа.
S1,S2,S3,S4 – каждому из этих состояний соответствует своя вероятность, нахождения системы в этом состоянии.
Пусть
-
вероятность того, что система в момент
времени t находится в
состоянии S1.
Интенсивность переходов:
,
где
-
время нахождения системы в данном
состоянии. Зададим малое приращение
и найдем вероятность
того, что в момент
система будет находиться в состоянии
S1.
Система была в момент времени t в состоянии S1 и за время никуда из этого состояния не ушла.
В момент времени t система была в состоянии S2 и за время перешла в состояние S1.
Рассмотрим вероятности этих состояний:
Возьмем предел от этой функции:
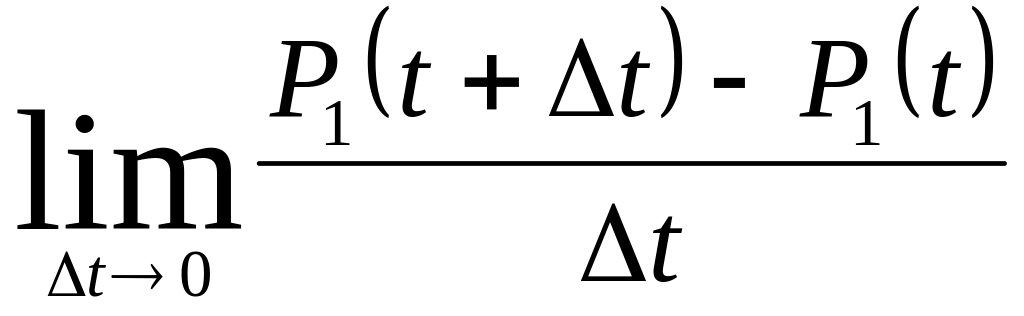
Таким образом, система уравнений Колмогорова имеет вид:
Общее правило составления дифференциальных уравнений Колмогорова
В левой части каждого уравнения стоит производная вероятности i-го состояния. В правой части сумма произведений вероятностей всех состояний, из которых идут стрелки в данное состояние на интенсивность соответствующих потоков событий минус произведение вероятности данного состояния на суммарную интенсивность всех потоков выводящих систему из данного состояния.
Начальные условия: P1(t)=1 P2(t)=P3(t)=P4(t)=0
Pi(t)=const (установившейся режим).
Для установившегося режима:
Это, так называемые, алгебраические уравнения Колмогорова.