Правила знаков.

Если внешняя сила стремится повернуть отсеченную часть балки по ходу часовой стрелки, относительно рассматриваемого сечения, то она вызывает положительную поперечную силу.

При рассмотрении правой отсеченной части:

- Q_y + F₂ – V_b = 0;

Q_y = -V_b + F₂.

Пример.

Построить эпюры Q и М для свободно лежащей балки пролетом «е», нагруженной сосредоточенной силой F (рисунок 12).

1. Определяем опорные реакции V_A и V_B:

∑М_А = 0; F*a – V_B*e = 0; V_B = F*a/e.

∑M_B = 0; V_A*e – F-b = 0; V_A = F*b/e.

Проверка: ∑Y = V_A – F + V_B = F-b/I – F + F*a/I = F/I(b – I + a) = 0.

2. Построение эпюры Q. Рассмотрим участок АС и сечение 1 – 1 на произвольном расстоянии Z. Алгебраическая сумма внешних сил, действующих слева от сечения:

Q₁ = V_A = F*b/e, так как эта сила постоянна и эпюра представляет прямую, параллельную оси Z.

3. Рассмотрим участок СВ и сечение 2 – 2. Алгебраическая сумма всех внешних сил, приложенных слева от сечения:

V_A – Q₂ – F = 0;

Q₂ = V_A – F = F*b/e – F = F/e(b - e) = -F*a/e = -V_B,

так как Q₂ – V_B = 0; Q₂ = V_B. Она также постоянна и поэтому эпюра Q параллельна оси Z.

На левой опоре действует положительная поперечная сила Q₁ = V_A. Откладываем ее значения F*b/I в принятом масштабе вверх, параллельно оси балок и проводим горизонтальную прямую до пересечения с линией действия силы F, которая направлена вниз, поэтому эпюра опускается в сечении С уступом на соответствующую величину. Далее проводим горизонтальную прямую до опоры В, где откладываем вверх ординату реакции V_B = F*a/I, тем самым замыкая эпюру. На построенной эпюре указываем алгебраические знаки и значения характерных ординат, после чего заштриховываем.

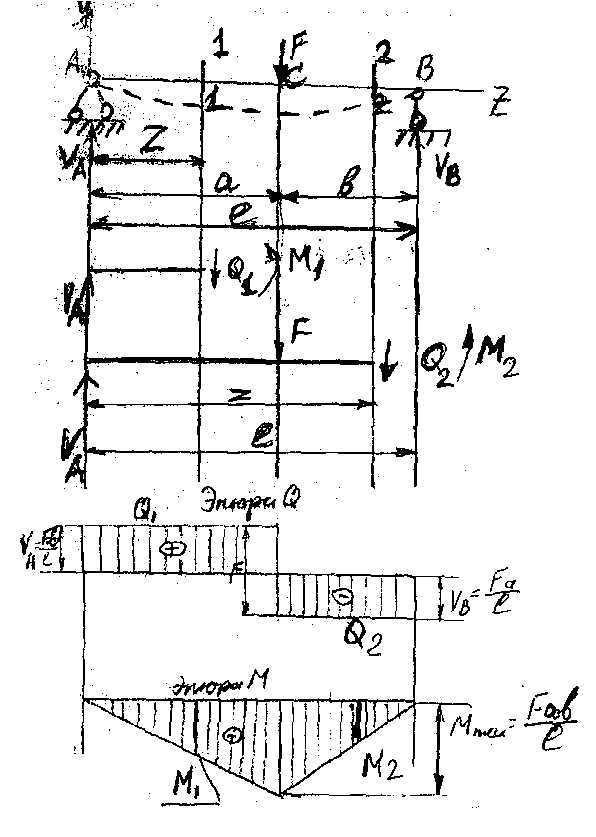
Рисунок 12.

Построение эпюры М: берем участок АС (0≤Z≤а); алгебраическая сумма моментов всех внешних сил, приложенных слева от сечения 1 – 1: M₁ = V_A*Z = (F*b/I)*Z; при Z = 0 M₁ = 0; при Z = a M₁ = F**b/I*a.

Рассматриваем участок АВ (a≤Z≤e): M₂ = V_A*Z – F(Z - a) = (F*b/I)*Z – f(Z - a); приZ = 0 M_C = (F*b/I)*a – F(a - a) = (F*b/I)*a. Получим то же значение изгибающего момента, что и на предыдущем участке; при Z = e M_b = (F*b/I)*I – F(I - a) = F*b – F*b = 0. После этого эпюру заштриховываем. Балка изгибается выпуклостью вниз, поэтому эпюра положительна.