
- •Примеры
- •5. Ограниченное снизу множество. Инфимум множества.
- •7. Свойство Архимеда. Плотное множество.
- •Неархимедово упорядоченное поле
- •8. Единственность поля действительных чисел. Расширенное множество действительных чисел.
- •10. Теорема Больцано – Вейерштрасса.
- •12. Окрестность точки. Внутренняя точка. Открытое и замкнутое множества.
- •13. Проколотая окрестность точки. Открытый и замкнутый интервалы.
- •15. Открытое покрытие. Теорема Гейн-Бореля.
- •Лемма Гейне — Бореля
- •16. Понятие функций. Область определения. Область значения.
- •17. Кольцо функций. Деление двух функций.
- •Примеры
- •Алгоритм Евклида
- •Свойства евклидовых колец
- •Свойства модулей над евклидовым кольцом
- •20. Односторонние пределы функций.
- •21. Пределы функций в бесконечности. Бесконечный предел.
- •22. Монотонная функция.
- •Условия монотонности функции
- •2) В. П. (н. П.) функции f(X) в точке x0 предел верхних (нижних) граней множеств значений функции f(X) в окрестности точки х0, когда эти окрестности стягиваются к точке х0. Он обозначается
- •Непрерывность функции в точке
- •Определение 25 (точки разрыва). A - точка разрыва f, если
- •28. Композиция двух функции и её непрерывность.
- •29. Ограниченная функция. Ограниченность непрерывных функции в замкнутом интервале.
- •Определение
- •37. Дифференцирование сложной функции.
- •38. Односторонние производные функции.
- •39. Экстремумы и точки перегиба функции.
- •Экстремумы
- •В ыпуклость и вогнутость.
- •40. Теорема Ролля.
- •Теорема (Ролля):
- •41. Теорема о промежуточном значении для производной.
- •Отношение бесконечно больших
- •43. Полином Тейлора. Остаточный член.
- •44. Теорема Тейлора.
- •45. Расширенная теорема о главном значении.
8. Единственность поля действительных чисел. Расширенное множество действительных чисел.
Расширенное множество действительных чисел
Множество ![]()
![]() ,
состоящее из элементов множества R и
двух символов -∞ и +∞, называется расширенной
системой действительных
чисел; причем выполняются следующие
условия:
,
состоящее из элементов множества R и
двух символов -∞ и +∞, называется расширенной
системой действительных
чисел; причем выполняются следующие
условия:
а) ![]()
![]()
![]()
![]()
![]()
![]() ;
;
б)
если a >
0, то ![]()
![]()
![]() ;
;
в)
если a <
0, то ![]()
![]()
![]() .
.
Символ -∞ (+∞) называется минус (плюс) бесконечностью.
Аксиомы
сложения На множестве вещественных
чисел, обозначаемом через ![]() (так
называемую R рубленую),
введенаоперация сложения («+»),
то есть каждой паре элементов (x,y) из
множества вещественных чисел ставится
в соответствие элемент x + y из
этого же множества, называемый
суммой x и y.
(так
называемую R рубленую),
введенаоперация сложения («+»),
то есть каждой паре элементов (x,y) из
множества вещественных чисел ставится
в соответствие элемент x + y из
этого же множества, называемый
суммой x и y.
 (коммутативность
сложения);
(коммутативность
сложения); (ассоциативность
сложения);
(ассоциативность
сложения); (существование
нейтрального элемента по сложению —
нуля);
(существование
нейтрального элемента по сложению —
нуля); (существование
противоположного элемента).
(существование
противоположного элемента).
Аксиомы
умножения На
введена
операция умножения («·»),
то есть каждой паре элементов (x,y) из
множества вещественных чисел ставится
в соответствие элемент ![]() (или,
сокращённо, xy)
из этого же множества, называемый
произведением x и y.
(или,
сокращённо, xy)
из этого же множества, называемый
произведением x и y.
 (коммутативность
умножения);
(коммутативность
умножения); (ассоциативность
умножения);
(ассоциативность
умножения);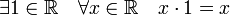 (существование
нейтрального элемента по умножению —
единицы);
(существование
нейтрального элемента по умножению —
единицы); (существование
обратного элемента).
(существование
обратного элемента).
Связь сложения и умножения
 (дистрибутивность
относительно сложения).
(дистрибутивность
относительно сложения).
Аксиомы
порядка На
задано
отношение порядка «![]() »
(меньше или равно), то есть для любой
пары x, y из
выполняется
хотя бы одно из условий
»
(меньше или равно), то есть для любой
пары x, y из
выполняется
хотя бы одно из условий ![]() или
или ![]() .
.
 ;
; ;
; .
.
Связь отношения порядка и сложения
 .
.
Связь отношения порядка и умножения
 .
.
Аксиома
непрерывности
![]()
Следствия аксиом
Непосредственно из аксиом следуют некоторые важные свойства вещественных чисел, например, единственность нуля, противоположного и обратного элементов.
9. Пиано постулаты и принцип математической индукций.
Словесная
1 является натуральным числом;
Число, следующее за натуральным, также является натуральным;
1 не следует ни за каким натуральным числом;
Если натуральное число непосредственно следует как за числом , так и за числом
 ,
то
и
тождественны;
,
то
и
тождественны;(Аксиома индукции) Если какое-либо предложение доказано для 1 (база индукции) и если из допущения, что оно верно для натурального числа , вытекает, что оно верно для следующего за натурального числа (индукционное предположение), то это предложение верно для всех натуральных чисел.
Математическая
Введём функцию ![]() ,
которая сопоставляет числу
следующее за
ним число.
,
которая сопоставляет числу
следующее за
ним число.
 ;
; ;
;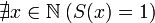 ;
; ;
; .
.
Или так:
;
 ;
; ;
; .
.
Формализация арифметики
Формализация арифметики включает в себя аксиомы Пеано, а также вводит число 0 и операции сложения и умножения с помощью следующих аксиом:
Принцип полной математической индукции
Существует также вариация, так называемый принцип полной математической индукции. Вот его строгая формулировка:
Пусть
имеется последовательность
утверждений ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Если для любого натурального
из
того, что истинны все
,
,
,
,
.
Если для любого натурального
из
того, что истинны все
,
,
,
, ![]() ,
следует также истинность
,
следует также истинность ![]() ,
то все утверждения в этой последовательности
истинны, то есть
,
то все утверждения в этой последовательности
истинны, то есть ![]() .
.
В
этой вариации база индукции оказывается
излишней, поскольку является тривиальным
частным случаем индукционного перехода.
Действительно, при ![]() импликация
импликация ![]() эквивалентна
.
Принцип полной математической индукции
является прямым применением более
сильнойтрансфинитной
индукции.
эквивалентна
.
Принцип полной математической индукции
является прямым применением более
сильнойтрансфинитной
индукции.
Принцип полной математической индукции также эквивалентен аксиоме индукции в аксиомах Пеано.
