22. Монотонная функция.
Монотонная функция — это функция, меняющаяся в одном и том же направлении.
Определения
Пусть
дана функция 
Тогда
функция называется возраста́ющей на , если
.
функция называется стро́го возраста́ющей на , если
.
функция называется убыва́ющей на , если
.
функция называется стро́го убыва́ющей на , если
.
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Свойства монотонных функций
Монотонная функция, определённая на интервале, измерима относительно борелевских сигма-алгебр.
Монотонная функция,
определённая
на замкнутом интервале, ограничена.
В частности, она интегрируема
по Лебегу.Монотонная функция может иметь разрывы только первого рода. В частности, множество точек разрыва не более чем счётно.
Монотонная функция
дифференцируема почти
всюду относительно меры
Лебега.
Условия монотонности функции
(Критерий монотонности функции, имеющей производную на интервале) Пусть функция
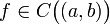непрерывна
на 
и
имеет в каждой точке 
производную 
Тогда
возрастает
на 
тогда
и только тогда, когда 
убывает
на
тогда
и только тогда, когда 
(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на и имеет в каждой точке производную Тогда
если 
то
строго
возрастает на 
если 
то
строго
убывает на 
Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на интервале Точнее имеет место
(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть
и
всюду на интервале определена
производная
Тогда
строго
возрастает на интервале
тогда
и только тогда, когда выполнены следующие
два условия:
Аналогично, строго убывает на интервале тогда и только тогда, когда выполнены следующие два условия:
1)
2)
23. Верхний и нижний пределы функций.
ВЕРХНИЙ И НИЖНИЙ ПРЕДЕЛЫ - 1) В. и н. п. последовательности - наибольший, и соответственно, наименьший, предел среди всех частичных пределов (конечных и бесконечных) данной последовательности действительных чисел. Для любой последовательности действительных чисел хn, n = 1, 2, ..., множество всех ее частичных пределов (конечных и бесконечных) на расширенной числовой прямой (т. е. в множестве действительных чисел, пополненном символами - ∞ и +∞) не пусто и имеет как наибольший, так и наименьший элементы (конечный или бесконечный). Наибольший элемент множества частичных пределов наз. верхним пределом (в. п.) последовательности и обозначается
наименьший элемент - нижним пределом (н. п.) и обозначается
Напр., если
хn = (-1)n,
то
если
хn = (-1)nn,
то
если
хn = n + (-1)nn,
то
У всякой последовательности существует в. п. (н. п.), при этом, если последовательность ограничена сверху (снизу), то ее в. п. (н. п.) конечен. Для того чтобы число а было в. п. (соответственно н. п.) последовательности хn, n = 1, 2, ..., необходимо и достаточно, чтобы для любого ε > 0 выполнялись условия: а) существует такой номер nε, что для всех номеров n ≥ nε справедливо неравенство хn < а + ε (хn > а - ε); б) для любого номера n0 существует такой номер n' = n'(ε, n0), что n' > n0 и хn' > а - ε (хn' < а + ε). Условие а) означает существование при любом фиксированном ε > 0 в последовательности {хn} лишь конечного числа таких членов хn, что хn > а + ε(хn < а - ε). Условие б) означает существование бесконечного множества таких членов хn, что хn > а - ε(хn < а + ε). Понятие н. п. сводится к понятию в. п. с помощью изменения знака у членов последовательности:
Для того чтобы последовательность хn, n = 1, 2, ..., имела предел (конечный или бесконечный, равный одному из символов - ∞ или +∞), необходимо и достаточно, чтобы
