Решение типовых задач для решения в аудитории
Сколькими способами можно выбрать 3 прибора из 6?
Решение. Поскольку порядок взятия приборов не играет роли, различные комбинации выбранных приборов отличаются только составом. Следовательно, число способов, которыми можно выбрать 3 прибора из 6, равно числу сочетаний из 6 по 3.
.
2. Карточка «Спортлото» содержит 49 чисел. Играющий зачеркивает 6 произвольных чисел по своему усмотрению. После тиража объявляется 6 «счастливых» чисел. В случае совпадения по крайней мере 3 зачеркнутых «счастливых» чисел владелец карточки получает выигрыш тем больший, чем больше чисел угадано. Максимальный выигрыш достигается, если удалось угадать все 6 чисел. Необходимо определить: а) сколькими способами можно зачеркнуть 6 чисел на карточке «Спортлото»? ; б) сколькими способами можно зачеркнуть 6 чисел на карточке «Спортлото» так, чтобы угадать 4 «счастливых» числа?; в) сколькими способами можно зачеркнуть 6 чисел на карточке «Спортлото» так, чтобы был обеспечен выигрыш?
Решение. Очевидно, что различные комбинации зачеркнутых чисел отличаются только составом, т. е. являются сочетаниями.
а) Общее число
различных способов выбора 6 чисел из 49
равно
.
Используя (3), получим
.
б) 4 «счастливых»
числа из 6 можно зачеркнуть
способами, 2 «несчастливых» числа из
(49-6) можно зачеркнуть
способами. Последовательный выбор 4 из
6 «счастливых» чисел и 2 из 43 «несчастливых»
на основании правила умножения может
быть выполнен
способами.
.
в) выигрыш достигается, если угадано или 3, или 4, или 5, или 6 «счастливых» чисел, т. е. выигрыш может быть достигнут четырьмя вариантами (то, что эти варианты отнюдь не равноценны для выигравшего, в условии данной задачи значения не имеет). Используя правило сложения, получим, что число способов, которыми можно зачеркнуть 6 чисел так, чтобы обеспечить выигрыш, равно
3.
Сколькими способами можно упорядочить
множество чисел
так, чтобы числа 1, 2, 3 стояли рядом в
порядке возрастания?
Решение. Числа
1, 2, 3 можно полагать склеенными в порядке
возрастания и рассматривать как один
элемент. Тогда число элементов множества
равно
и они могут быть упорядочены
способами (число перестановок из
элементов).
4.
Сколькими различными способами можно
разбросать
шариков по
лункам так, чтобы в первую лунку попало
шариков, во вторую -
шариков …, в
–
ю -
шариков
?
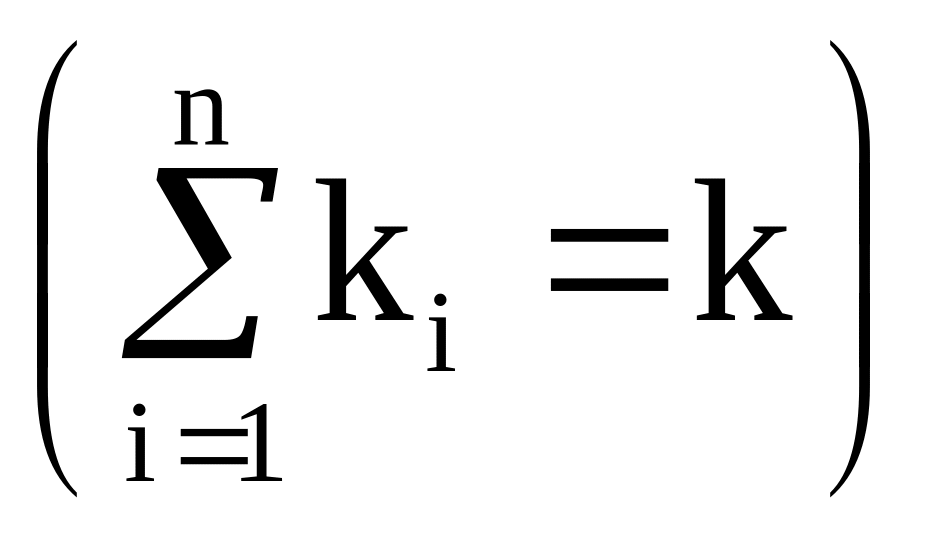Решение.
Каждый шарик независимо от других
выбирает себе лунку. Эту операцию он
может выполнить
способами. (Схема, в которой каждая
лунка выбирает шарики, приводит к выбору
с очень сложной взаимной зависимостью).
Таким образом, речь идет о выборках с
возвращением объема
из
элементов генеральной совокупности,
причем выборки различаются только
порядком, а состав их одинаков.
(Пронумерованными считаются не только
лунки, но и шарики, номера которых и
определяют порядок взятия лунок).
Следовательно, число таких выборок
равно числу
перестановок с повторениями и может
быть определено по формуле (11):
.
5. Сколькими различными способами можно разбросать 4 шарика по 3 лункам?
Решение. Так же, как и в предыдущей задаче, каждый шарик независимо от других выбирает себе лунку, т. е. идет речь о выборках возвращениями объема 4
из 3 элементов. Но
далее условие задач неоднозначно.
По-видимому, вполне естественно считать
лунки пронумерованными (различными).
Однако шарики можно считать и
пронумерованными, и непронумерованными.
Соответственно выборки различаются
или порядком и составом элементов, или
только составом. В первом случае число
различных выборок равно числу
размещений с повторениями из 3 элементов
по 4. При этом, в соответствии с (9), получим
.
Во втором случае число различных выборок равно числу сочетаний с повторениями из 3 элементов по 4. При этом в соответствии (12) находим
.