
- •Глава XIV Теория аналитических функций.
- •§79. Функции и функциональные ряды. Элементарные функции.
- •§80. Производная и интеграл.
- •§80. Производная и интеграл (продолжение).
- •§81. Интеграл Коши и его следствия.
- •§ Ряд Лорана и изолированные особые точки однозначных аналитических функций.
- •§83. Вычеты и их приложения.
- •Конформные отображения
Глава XIV Теория аналитических функций.
Комплексное число z=x+iy, отличное от нуля можно записать в тригонометрической форме:
![]() ,
где
,
где
![]() -
модуль комплексного числа z,
Arg
z
– аргумент этого числа.
-
модуль комплексного числа z,
Arg
z
– аргумент этого числа.
Значение аргумента заключенное в промежутке (-π, π], называется главным значением аргумента и обозначается arg z.
Аргумент комплексного числа вычисляется по формуле:
![]() (
(![]() ),
где –π<arg
z
),
где –π<arg
z![]() π.
π.
Главное значение аргумента числа z=x+iy можно вычислить по формулам:
![]() ,
при x>0,
,
при x>0,
![]() ,
при x<0,
y
,
при x<0,
y![]() 0,
0,
![]() ,
при x<0,
y<0.
,
при x<0,
y<0.
№2664. Найти модули и главные значения аргумента комплексных чисел, заданных ниже. Записать эти числа в тригонометрической форме:
z=1+i
![]()
![]() (т.к.
x>0)
(т.к.
x>0)
![]()
3) z=3
![]()
![]()
![]()
5) z=6i
![]()
![]()
![]()
7) z=-1+i
![]()
![]()
![]()
9)
![]()
![]()
![]()
![]()
11)
![]()
![]()
![]()
![]()
13)
![]()
![]()
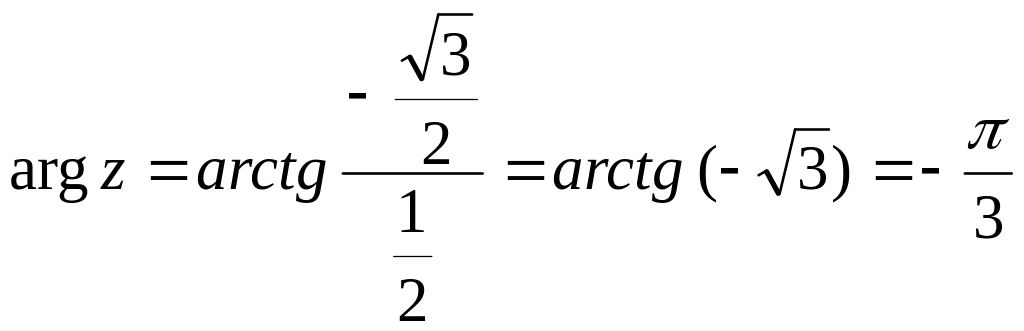
![]()
Корень n-ой
степени из комплексного числа
![]() ,
отличного от нуля имеет n
значений. Все они определяются по
формуле:
,
отличного от нуля имеет n
значений. Все они определяются по
формуле:
![]() (k=0;+1;…;n-1)
(k=0;+1;…;n-1)
№2665. Найти все значения корней, заданных ниже комплексных чисел, и изобразить их в виде точек комплексной плоскости:
1)
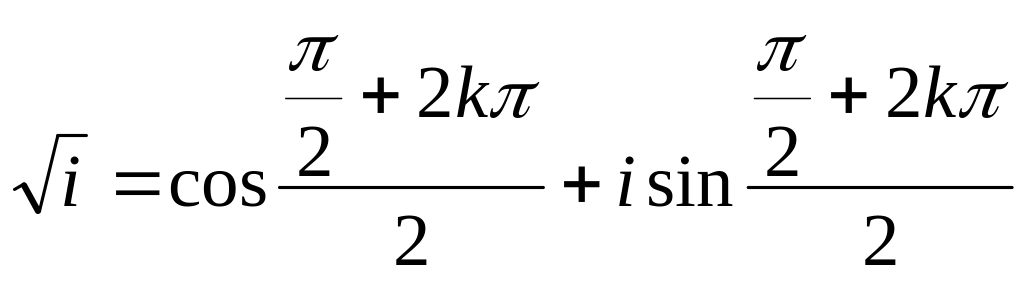 (k=0;1)
(k=0;1)
(![]()
![]() )
)
k=0,
![]()
k=1

3)
![]() ,
z=-1,
,
z=-1,
![]() ,
,
![]()
![]() (k=0,1,2)
(k=0,1,2)
k=0,
![]()
k=1,
![]()
k=2,
![]()
5)
![]() (k=0,1,2,3)
(k=0,1,2,3)
k=0,
![]()
k=1,
![]()
k=2,
![]()
k=3,
![]()
7)
![]() ,
z=
,
z=
![]()
![]()
![]()
![]()
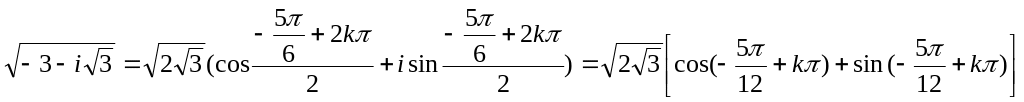 (k=0,1)
(k=0,1)
k=0,
![]() ;
;
k=1,
![]()
9)
![]() ,
z=2-i2
,
z=2-i2 ![]()
![]()
![]()
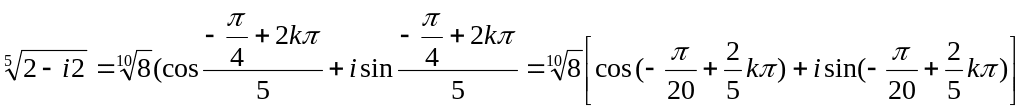
(k=0,1,2,3,4)
В задачах 2675-2684 требуется найти множество точек в комплексной плоскости (Z), удовлетворяющих соответствующему равенству:
№2675
![]() - окружность с
центром в точке z0
радиуса R.
- окружность с
центром в точке z0
радиуса R.
![]()
![]() =R2
=R2
№2677
|z+1-2i|=3 – окружность с центром в точке -1+2i радиуса 3.
![]()
![]()
№2679.
Re z - Im z =2
x – y =2 => y = x – 2 - прямая.
№2681.
|z - 1| + |z + 1| =3
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
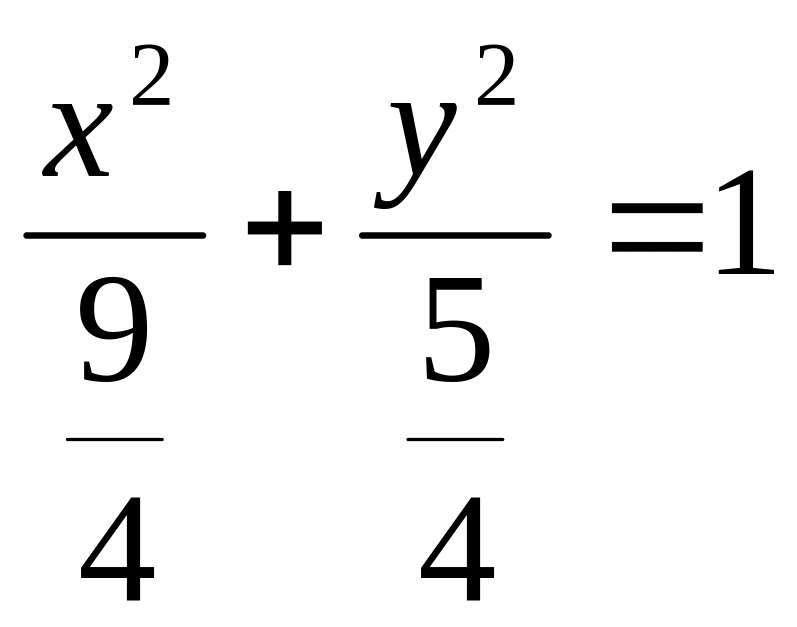 ,
,
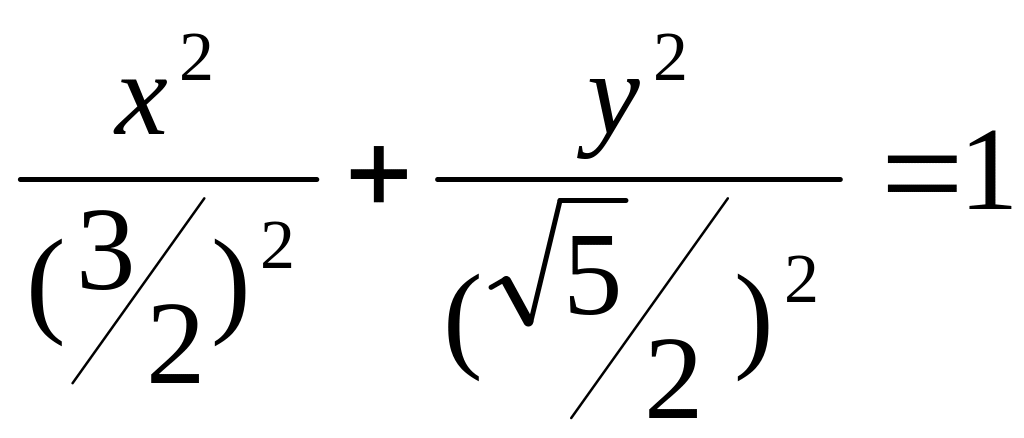
№2683.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
В задачах 2685-2696 требуется найти множество точек в комплексной плоскости (Z), удовлетворяющих соответствующему неравенству:
№2685.
|z
- z0|<R,
![]() ,
,
![]() - внутренность круга с центром в точке
z0
радиуса R.
- внутренность круга с центром в точке
z0
радиуса R.
№2687.
|z +1- i| <3
![]() ,
,
![]() - внутренность круга с центром в точке
- внутренность круга с центром в точке
![]() радиуса
3.
радиуса
3.
№2689.
Re z > 2, x>2 – полуплоскость расположенная справа от прямой x=2.
№2690.
![]() ,
,
![]() - прямая y=-1
и полуплоскость расположенная ниже
этой прямой.
- прямая y=-1
и полуплоскость расположенная ниже
этой прямой.
№2691.
0<Re z<2, 0<x<2 – полоса расположенная между прямыми x=0,x=2.
№2692.
![]() ,
,
![]() - прямые y=0,
y=3
и все точки между ними.
- прямые y=0,
y=3
и все точки между ними.
№2693.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Парабола y2=1-2x и её внутренность.
№2695.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Угол, образованный
положительной частью действительной
оси и лучом, выходящим из начала координат
и образующим с положительным направлением
действительной оси угол, равный
![]() радиана, а также точки, лежащие на
сторонах этого угла.
радиана, а также точки, лежащие на
сторонах этого угла.
Для того чтобы
сходился (абсолютно сходился) ряд
![]() ,
необходимо и достаточно, чтобы сходились
(абсолютно сходились) ряды
,
необходимо и достаточно, чтобы сходились
(абсолютно сходились) ряды![]() и
и
![]() .
.
§79. Функции и функциональные ряды. Элементарные функции.
Функция
![]() в точке
в точке
![]() имеет предел C
= A
+ i
B,
тогда и только тогда, когда функции
u(x,y)
и v(x,y),
рассматриваемые как действительные
функции двух действительных переменных
x
и y,
имеют в точке (x0,y0)
пределы равные соответственно A
и B.
имеет предел C
= A
+ i
B,
тогда и только тогда, когда функции
u(x,y)
и v(x,y),
рассматриваемые как действительные
функции двух действительных переменных
x
и y,
имеют в точке (x0,y0)
пределы равные соответственно A
и B.
Существуют ли пределы в точке z=0 функций, данных в задачах 2713 – 2716?
№2713
![]() (нет)
(нет)
№2714
![]() (нет)
(нет)
№2715
![]() (нет)
(нет)
№2716
![]() (да)
(да)
№2717
В каких точках
комплексной плоскости (Z)
не существует предела функции
![]() (главное
значение аргумента z)?
(главное
значение аргумента z)?
Ответ: во всех точках неположительной части действительной оси (т. к. при движении по часовой стрелке предел равен -π, а против часовой π).
Функция непрерывна в точке тогда и только тогда, когда обе функции u(x,y) и v(x,y), рассматриваемые как действительные функции двух действительных переменных x и y, непрерывны в точке (x0,y0).
Функции exp z, sin z, cos z определяются с помощью равенств:
![]()
![]()
![]()
Функции exp z, sin z, cos z связаны равенствами:
![]()
![]()
![]()
носящими название формул Эйлера. Для этих функций справедливы также равенства:
![]()
![]()
![]()
для любых z1 и z2.
По определению гиперболическим синусом и гиперболическим косинусом называются соответственно функции:
![]()
![]()
Комплексное
число
![]() может
быть записано в показательной форме:
может
быть записано в показательной форме:
![]() (4)
(4)
№2747.
Использую формулу (4), представьте в показательной форме комплексные числа:
1) z=-1, |z|=1, arg z=π
![]()
3) z=-i,
,
![]()
![]()
5) z=1-i,
![]() ,
,
![]()
![]()
7)
![]() ,
,
![]() ,
,
![]()
![]()
Все значения
логарифма комплексного числа
![]() содержатся
в равенстве
содержатся
в равенстве
![]() (
(![]() ),
),
где
![]() - главное значение логарифма.
- главное значение логарифма.
Для любых
комплексных чисел
![]() и α по определению:
и α по определению:
![]()
![]() (
)
(
)
![]()
![]()
(при z1=z2=z≠0, Ln 1=Ln z – Ln z, т. е. Ln 1 = 2k π i ( )
№2748. Найти все значения нижезаданных выражений:
1)
![]() (
)
(
)
3)
![]() (
)
(
)
5)
![]() (
)
(
)
7)
![]()
(![]() ,
где α –
действительное число)
,
где α –
действительное число)
8)
![]()
![]()
