3. Математическая модель цифрового фильтра высоких частот

В соответствии с заданием нам необходимо реализовать фильтр верхних частот первого порядка. Передаточная функция его имеет вид:

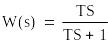
(3.1)

Частота среза при которой ослабление амплитуды составляет 2^0,5, определяется выражением:

f_с=1/2πТ, (3.2)

Из (3.2) находим временную постоянную Т

T=1/2π f_с=1/2 3,14 0,1=1,59 (с), отсюда

(3.3)

В программе Matlab выполнено моделирование передаточной функции 3.3.

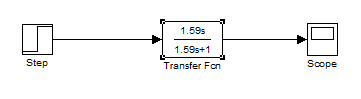
Рис.3.1. Схема исследования фильтра высоких частот

При исследовании передаточной функции, на вход подавалось единичное возмущение.

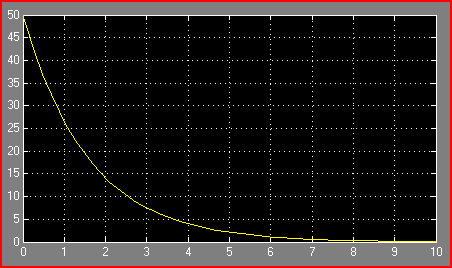
Рис.3.2. Переходный процесс на выходе фильтра высоких частот при моделировании

Наиболее естественной формой описания дискретных схем являются разностные уравнения. При этом говорят, что задан цифровой фильтр N-го порядка, если работа схемы может быть описана разностным уравнением вида:

F(y_n ,y_n-1 ,...,y_n-N ,x_n ,x_n-1 ,...,x_n-M)=0, (3.4)

где y_n-k ,x_n-k - значения выходной и входной координат, отстоящих в прошлое на интервал k t.

Кроме того, считают, что MN.

Если функция F линейна относительно всех своих координат, то говорят о линейном цифровом фильтре, разностное уравнение для которого может быть записано так:

y_n=b₁ y_n-1 +b₂ y_n-2 +...+b_N y_n-N +a₀ x_n +a₁ x_n-1 +...+a_M x_n-M , (3.5)

где b_i , a_{i -}действительные числа.

Другим способом задания ЦФ является описание с помощью Z-передаточной функции:

(3.6)

Уравнение (3.5) является готовым алгоритмом работы ВУ для получения текущего значения выходной координаты y_n по значениям входной и выходной координат в предшествующие моменты времени, и поэтому, почти всегда, любую математическую модель ЦФ стремятся свести именно к такому виду.

Задача проектирования ЦФ существенно упрощается, если частота выборки входного сигнала существенно больше частоты высшей гармоники во входном сигнале:

, (3.7)

и если между величиной дискретизации сигнала по уровню _мр и максимальном значением входного сигнала X_max выполняется соотношение:

_мр<< X_max . (3.8)

При этом внешнее описание ЦФ, как преобразователя аналогового сигнала, может быть задано в виде дифференциального уравнения или в виде соответствующей передаточной функции W(S).

Внутреннее описание фильтра (для разработки программы работы ВУ) все равно удобно иметь в виде разностного уравнения.

Для перехода от дифференциального уравнения к разностному можно воспользоваться “машинными” производными, отличающимися от обычных тем, что разность аргументов в знаменателе не стремится к нулю, а равна интервалу дискретизации t:

(3.9)

и т.д.

Ощибка вычисления производной тем меньше, чем меньше интервал t.

Величина t равна времени выполнения одного цикла получения значения выходной величины. Оно может быть оценено по числу и типу команд, составляющих данный цикл вычислений, и уточнено после экспериментальной проверки работы ЦФ, как промежуток времени между двумя соседними выдачами выходного сигнала.

Если условия (3.7) и (3.8) не удовлетворены, то проектирование ЦФ по дифференциальному уравнению может дать недопустимо большую ошибку в работе фильтра. В этом случае следует использовать аппарат Z-передаточных функций, но, во всяком случае, интервал t ограничивается теоремой Котельникова. Смысл ее в том, что сигналы, с ограниченным частотой f_max спектром, могут быть однозначно представлены последовательностями своих значений, взятых через интервал времени, удовлетворяющий соотношению:

, (3.10)

причем само это представление таково:

где t_k=k t.

Понятно, что точное описание функции y(t) требует использования бесконечно большого количества значений y(t_k) как до, так и после интересующего нас момента времени. Однако, для большинства технических задач обеспечить приемлемую точность можно, используя только несколько предыдущих значений, причем тем меньшее их число, чем меньше интервал дискретности t. Считается достаточным, если частота опроса на порядок выше величины f_max:

, (3.11) .

Так как рассматриваемая передаточная функция (3.1) есть ни что иное, как фильтр верхних частот. Частотой среза, в соответствии с заданием, равна f_с =0,1 Гц, тогда

∆t≤1/10 0,1=1 (с);

Выбираем значение интервала дискретизации t = 100 мс.

Перейдем от дифференциального уравнения к разностному уравнению. Передаточная функция имеет вид:

1,59dy/dt + y = 1,59dx/dt,

Для упрощения вычислений, вернемся к Т=1,59.

Для перехода от дифференциального уравнения к разностному, точное значение производной заменяется "машинным" эквивалентом:

T(y_n-y_n-1)/∆t+y_n= T(x_n-x_n-1)/∆t,

обозначим Т/∆t=А₀,

тогда А₀(y_n-y_n-1)+y_n= А₀ (x_n-x_n-1),

y_n(А₀+1) - А₀ y_n-1= А₀ (x_n-x_n-1),

y_n= (А₀( x_n-x_n-1) + А₀ y_n-1)/ (А₀+1),

подставив известное значение А₀=15,9,

тогда получим y_n= (15,9 ( x_n-x_n-1) + 15,9 y_n-1)/16,9,

для того, чтобы избавиться от дробной части, умножим числитель и знаменатель на 10:

y_n= 159( ( x_n-x_n-1) + y_n-1)/169.

Построим переходный процесс, который получен в результате расчета по разностному уравнению.

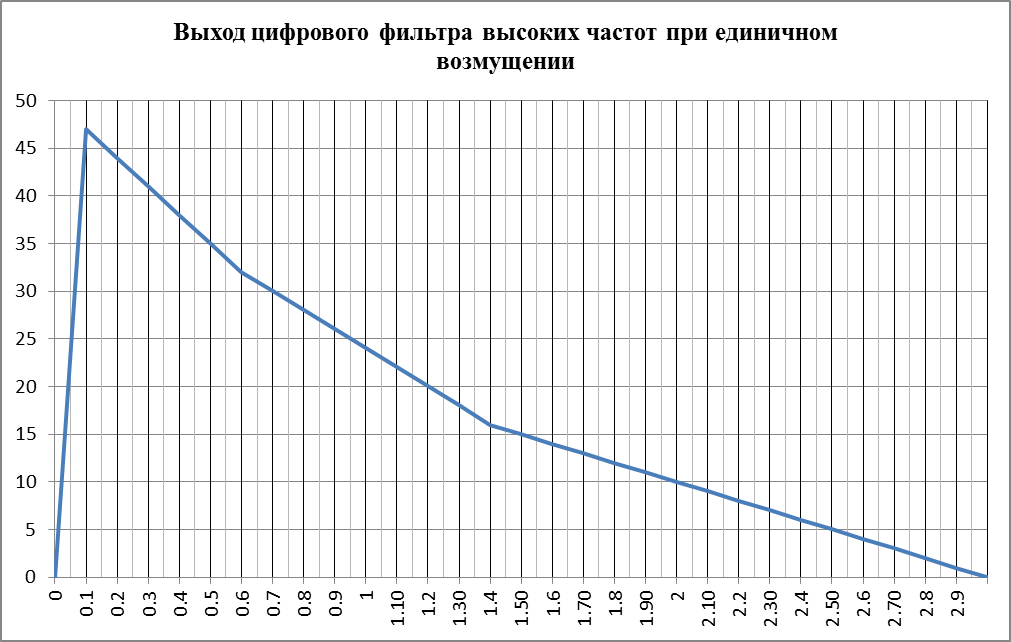
Рис.3.3. Переходный процесс на выходе цифрового фильтра высоких частот

4. Б лок-схема алгоритма работы устройства

\Описание алгоритма работы устройства:

1. Инициализация. Инициализация программы заключается в задании начальных значений и установке в нуль программных переменных (адресов, счетчиков, переключателей, указателей и т. п.) перед выполнением программы. Определение начальных значений при первом описании переменной.

2. Измерение сигналов с выходов датчиков. Аналоговые сигналы подаются в порты ввода, где они записываются в регистры RW0, RW1, RW2.

3. Масштабирование сигналов. Для преобразования сигнала в цифровой код, масштабируем сигнал и смещаем для получения диапазона 0÷5 В.

4. Восстановление отрицательных значений. Для корректной работы фильтра в программе нужно предусмотреть процедуру восстановления отрицательных значений путём вычитания из входного кода числа, соответствующего смещению.

5. Вычисление выходного сигнала по каждому каналу

y_n= 159( ( x_n-x_n-1) + y_n-1)/169_.

Вычисление сводится к разработке подпрограмм умножения и сложения дробных чисел.

6. Преобразование в целое. Преобразование дробных чисел в целые.

7. Вывод чисел в ЦАПы. Преобразование цифровых сигналов в аналоговые.

8. Производится вычисление неисправного сигнала.

9. При исправности 1 канала выводится этот сигнал на выход.

10. При неисправности 1 канала производится контроль исправности 2 канала путём сравнения 2 сигнала с 1 и 3 сигналом.

11. При исправности 2 канала выводится этот сигнал на выход.

12. При неисправности и 2 канала производится контроль исправности 3 канала путём сравнения 3 сигнала с 1 и 2 сигналом.

13. При исправности 3 канала выводится этот сигнал на выход.

14. При неисправности и 3 канала производится сигнализация «Неисправность системы».