Октарные и бинарные деревья
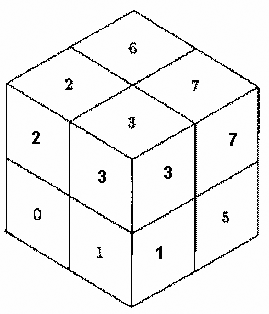
За основу берется куб, в который вписано тело. Куб разбивается на восемь подкубов-октантов, которые нумеруются как показано на рисунке. Октантам присваивается «цвет»:
Белый – октант пуст (лист);
Черный – октант заполнен полностью (лист);
Серый – октант заполнен ЧАСТИЧНО
Для «серых» октантов пространство дальше разбивается рекурсивно.
ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОКТАРНОГО ДЕРЕВА
Для тела, показанного на рисунке выше, дерево октантов выглядит так:
СМЫСЛ РАСКРАСКИ:
Белый – октант пуст (лист);
Черный – октант заполнен полностью (лист);
Серый – октант заполнен ЧАСТИЧНО (промежуточный узел дерева).
Удобство графического вывода состоит в том, что, выбирая определенный порядок вывода октантов (соответствующий их упорядоченности по глубине), можно рисовать сцену методом «плывущего горизонта» и избежать таким образом трудоемкого удаления невидимых линий и граней.
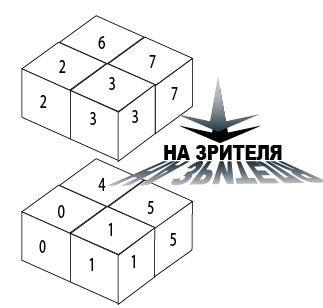
Здесь имеет место такая УПОРЯДОЧЕННОСТЬ ОКТАНТОВ ПО ГЛУБИНЕ:
4, 0, 5, 1, 6, 2, 7, 3
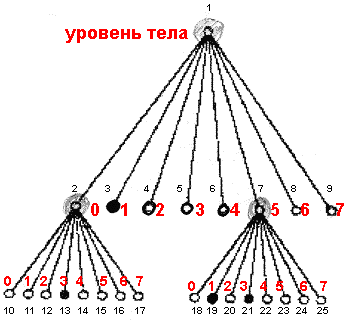
ЛИНЕЙНОЕ ПРЕДСТАВЛЕНИЕ ОКТАРНОГО ДЕРЕВА
Это октарное дерево можно задать такой линейной записью. Б=белый узе, Ч= черный узел, стрелка = переход на уровень вниз к составляющим
Двоичное дерево деления пространств
Бинарное разделение пространства тоже возможно, вводят такую дисциплину: сначала объем делят пополам вдоль оси Х, потом кахжую половину пополам влоль оси Y, затем каждую четвертину еще раз пополам вдоль оси Z.
Каждую из восьмушек далее рекурсивно делят с той же последовательностью разделений. Двоичное дерево ля рассмотренного выше примера:
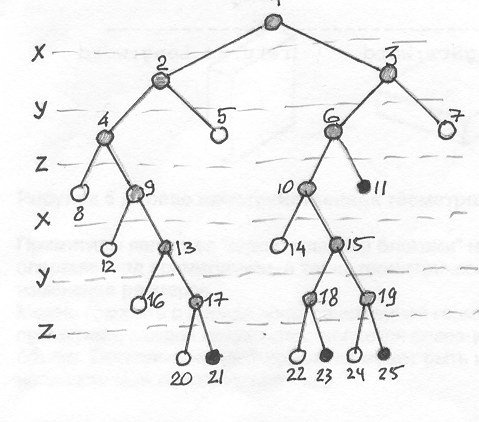
…И его линейное представление
КОНСТРУКТИВНАЯ ГЕОМЕТРИЯ
Метод моделирования трехмерных тел с помощью параметризованных примитивов (CSG – Compositional Space Geometry ) напоминает по логике игру «в кубики». Для получения сложных тел программа моделирования должна быть в состоянии выполнять с примитивами и их объединениями теоретико-множественные операции объединения, вычитания, пересечения и т.п.
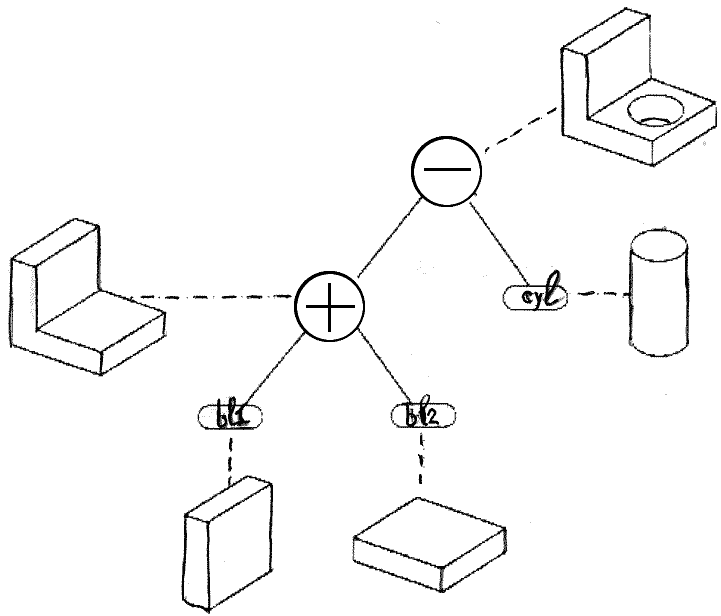Пример
применения CGM.
ГРАНИЧНОЕ ПРЕДСТАВЛЕНИЕ
Трехмерное тело задается своей поверхностью. Как правило, это отсеки плоскостей, но теоретически рассматриваются и отсеки бикубических параметрических поверхностей. Нормали к каждой грани должны быть направлены внутрь тела. Пример параллелепипеда:
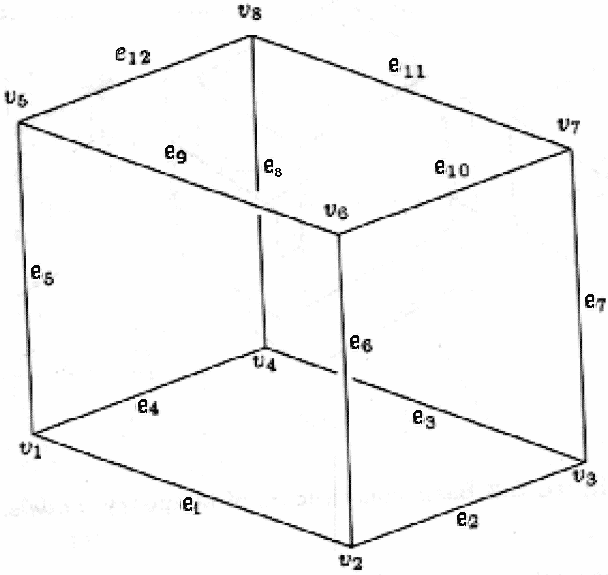
Списком вершин
Если задавать тело только списком вершин, то нет возможности восстановить ни ребра, ни грани:
Слишком мало информации.
Списком ГРАНЕЙ
При задании тела только списком граней, задаваемых как последовательность вершин, то информации уже больше. Но в таком описании информация о ребрах содержится только НЕЯВНО.
Каноническое (три уровня)
Для целей визуализации трехмерных тел лучше всего подходит трехуровневое описание, которое считается каноническим.
Верхний уровень – список граней. Каждая грань задается списком указателей на ребра, которые его ограничивают.
Средний уровень – список ребер. Каждое ребро задается парой указателей на вершину-начало и вершину-конец ребра.
Нижний уровень – список вершин. Каждая вершина задается тройкой своих координат в системе координат сцены («мировая» система координат).
Достоинством этой схемы есть то, что средний и верхний уровни – топологические, а нижний – физический. При перемещениях и др. преобразованиях тела пересчетам подвергается только уровень вершин, два верхних уровня остаются без изменений.