§2. Определенный интеграл.
2.1. Понятие интегральной суммы.
Пусть функция f(x) определена на отрезке [a, b] оси Ох. Произвольным образом разобьем отрезок [a; b] на п равных частей точками
х0=а, х1, х2, …, хп-1, хп=b, где х0<х1<х2< …< хп-1< хп.
Полученные в результате разбиения отрезки [х0, х1], [x1,x2], …, [хп-1, хп] назовем элементарными, а их длины обозначим соответственно через ∆х1=х1 – х0, ∆х2=х2 – х1, …, ∆хп=хп – хп-1.
Выберем произвольным образом точку с1 на отрезке [х0, х1], точку с2 на отрезке [x1,x2],…, точку сп на отрезке [хп-1, хп] и вычислим соответствующие значения функции f(x) в этих точках, то есть найдем f(с1), f(с2), …, f(сп).
Составим сумму попарных произведений найденных значений функции на длины соответствующих элементарных отрезков, т.е. сумму вида
f(с1)∆
х1
+ f(с2)∆
х2+
…+ f(сi)∆
хi
+…+ f(сп)∆хп
=
f(сi)∆хi
(2.1.1)
Сумма (2.1.1) называется интегральной суммой для функции f(x), составленной на отрезке [a, b].
Очевидно, что интегральная сумма зависит как от способа разбиения данного отрезка [a, b] на элементарные отрезки, так и от выбора точек сi на каждом из полученных элементарных отрезков.
Следовательно, для данной функции f(x) на данном отрезке [a, b] можно составить бесчисленное множество интегральных сумм.
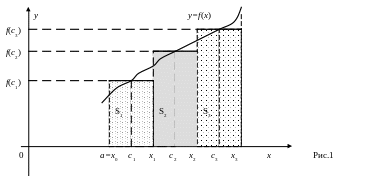
2.2. Геометрический смысл интегральной суммы
Пусть функция f(x) неотрицательна на отрезке [a; b].
Отдельное слагаемое f(сi)∆хi интегральной суммы (2.1.1) в этом случае равно площади Si прямоугольника со сторонами f(сi) и ∆хi , где i=1, 2, …, n (см. рис. 1, где х1 – х0 = ∆х1, х2 – х1 = ∆х2, и т.д.).
Другими словами, Si − это площадь под кривой у=f(сi) на отрезке [хi-1; хi]. Поэтому вся интегральная сумма (2.1.1) равна площади Sл = S1+ S2+ …+Sn под ломаной, образованной на каждом их отрезков [хi-1; хi] прямой у=f(сi), параллельной оси абсцисс.
2.3. Понятие определенного интеграла
Для избранного разбиения отрезка [a; b] на части обозначим через max ∆хi наибольшую из длин элементарных отрезков.
Если интегральная
сумма (2.1.1) при max
∆хi
0
имеет конечный предел, не зависящий ни
от способа разбиения отрезка [a;
b]
на элементарные отрезки, ни от выбора
точек сi
на этих
элементарных отрезках, то этот предел
называется определенным
интегралом
функции f(x)
на отрезке [a;
b]
и обозначается символом
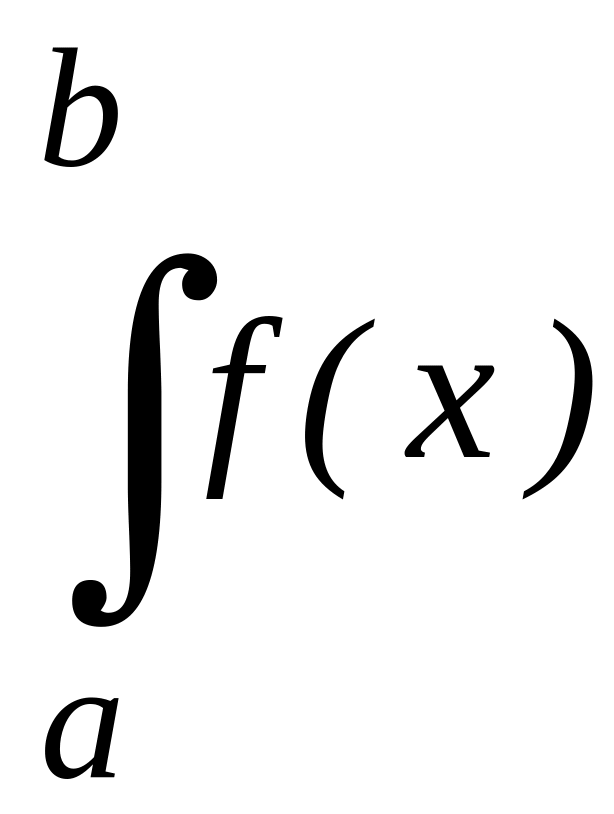dx.
Таким образом, по определению имеем
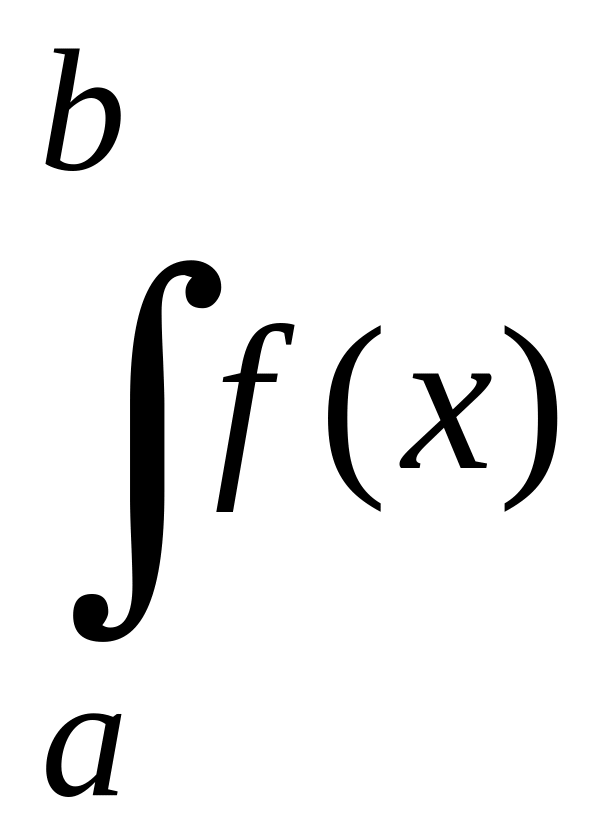dx
=
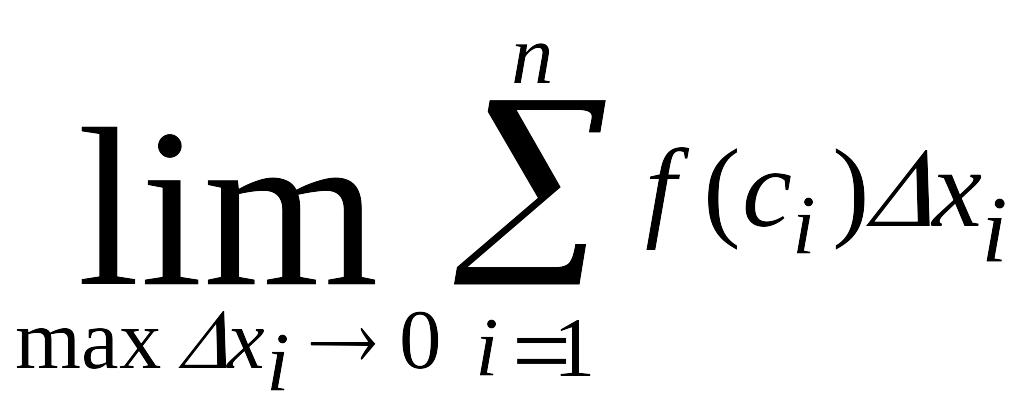(2.3.1)
В равенстве (2.3.1) числа а и b называются соответственно нижним и верхним пределами интегрирования, отрезок [a; b] – отрезком интегрирования, функция f(x) – подынтегральной функцией, выражение f(x)dx – подынтегральным выражением, х – переменной интегрирования.
Функция f(x), для которой на отрезке [a; b] существует определенный интеграл, называется интегрируемой на этом отрезке.
Сформулируем теорему существования определенного интеграла.
Теорема 2.1 (Коши).
Если функция у=f(x)
непрерывна на отрезке [a;
b], то
определенный интеграл
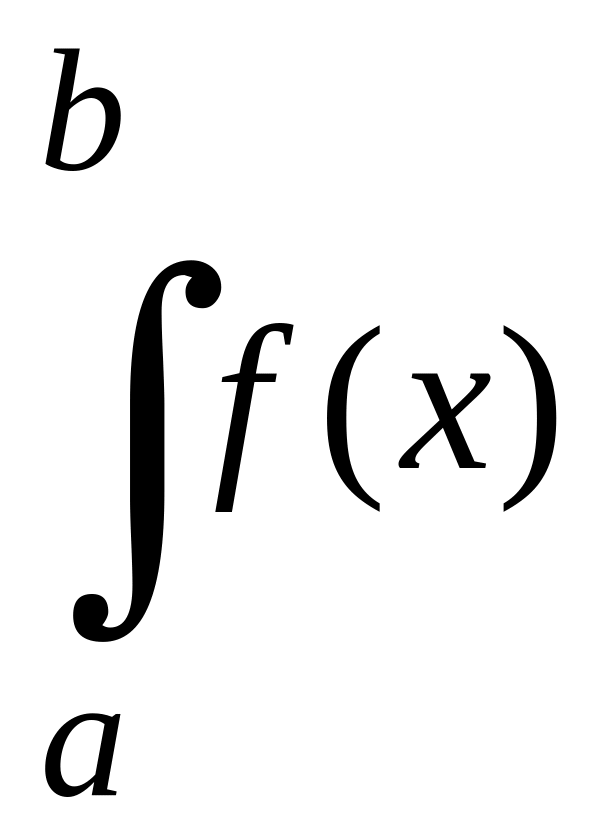dx
существует. (без
доказательства)
Эта теорема выражает достаточное условие интегрируемости функции.