4.2. Несобственный интеграл іі рода.

Пусть функция f(x) непрерывна на промежутке [a; b) и имеет бесконечный разрыв при х = b.

Если существует конечный предел , то его называют несобственным интегралом второго рода и обозначают dx.

Таким образом, по определению, dx= .

Если предел в правой части существует, то несобственный интеграл dx сходится. Если же указанный предел не существует или бесконечен, то говорят, что интеграл dx расходится.

Аналогично, если функция f(x) терпит бесконечный разрыв в точке х=а, то полагают dx= dx.

Если функция f(x) терпит разрыв во внутренней точке с отрезка [a; b], то несобственный интеграл второго рода определяется формулой

dx = dx + dx.

В этом случае интеграл слева называют сходящимся, если оба несобственных интеграла, стоящих справа, сходятся.

В случае, когда f(x)>0, несобственный интеграл второго рода dx (разрыв в точке х=b) можно истолковать геометрически как площадь бесконечно высокой криволинейной трапеции (см. рис.11).

П ример. Вычислить .

Решение

При х=0 функция у= терпит бесконечный разрыв;

= dx =

= , интеграл расходится.

Признаки сходимости для несобственных интегралов второго рода.

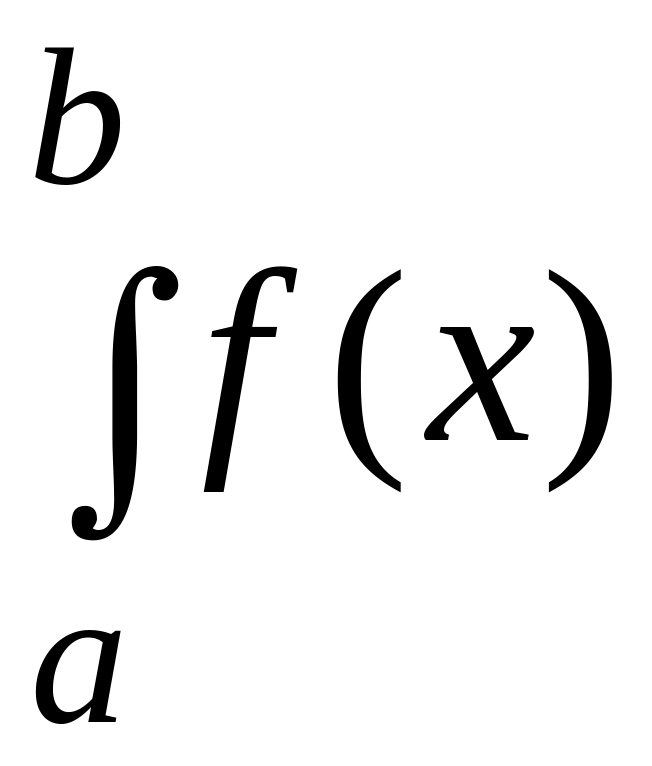Теорема 4.2.1. Пусть на промежутке [a; b) функции f(x) и (х) непрерывны, при х=b терпят разрыв и удовлетворяют условию 0 ≤ f(x) ≤ (х). Из сходимости интеграла dx вытекает сходимость интеграла dx, а из расходимости интеграла dx вытекает расходимость интеграла dx.

Теорема 4.2.2. Пусть функции f(x) и (х) непрерывны на промежутке [a; b) и в точке х=b терпят разрыв. Если существует предел , 0<k< , то интегралы и одновременно сходятся или одновременно расходятся.