1.2 Решения фирм

Вторая часть модели состоит из решений фирм. Фирмы минимизируют издержки производства и максимизируют прибыль.

Минимизирование издержек фирмы:

Предполагается, что труд – единственный фактор производства. Таким образом, выпуск фирмы зависит только от объема используемого труда и технологий . Фирма j минимизирует издержки, выбирая минимально возможный уровень занятости при условии, что она будет производить определенный товар , выпуск которого задается функцией производства. Математически имеем:

(21)

_{при условии}

(22)

где переменная в функции производства (22) - это агрегированная производительность, которая предполагается стохастической (как видно, агрегированная производительность для всех фирм одинакова). Таким образом, предполагается постоянная отдача от масштаба (Carl Walsch, 2003).

Используя Лагранжиан

(23)

где - реальные предельные издержки. Получаем условие первого порядка:

(24)

Итак, мы определили, что предельные издержки фирмы равняются реальной заработной плате разделенной на предельный продукт труда .

Максимизация прибыли фирм:

На втором этапе фирмы максимизируют прибыль, которая определяется как разница между доходом от продажи индивидуального блага и издержек производства данного блага, , устанавливая цены на свои индивидуальные блага при условии, что (кривая) спрос на их индивидуальные товары задается формулой (8) и предпосылке о том, что цены жесткие. Согласно Кальво³⁵ (Calvo) (1983), в каждом периоде часть фирм не может изменить свои цены и вынуждена придерживаться цен, выбранных в каком-то предыдущем периоде, а другая часть фирм может пересмотреть свои цены. Параметр - это мера степени номинальной жесткости цен: чем больше , тем меньше фирм могут пересматривать цены в каждом из периодов и тем больше ожидаемое время до последующего пересмотра цен (фирмы, которые могут менять цены в периоде t, максимизируют ожидаемую дисконтированную текущую и будущие прибыли; прибыли в будущем, например, в периоде t+s, зависят от выбора цен в периоде t только в том случае, если фирма не получила возможности изменить свои цены в любом из периодов между t и t+s; вероятность данного события равна ). Математически проблему максимизации прибыли можно выразить следующим образом:

(25)

при условии

(8)

с учетом предпосылки Кальво (Calvo). Заметим, что соответствующий фактор дисконтирования в (25) задается как ³⁶, то есть равен величине обратной к ожидаемой реальной доходности, полученной за периодов.

Подставляя (кривую) функцию спроса (8) в (25) и используя цены Кальво, получаем:

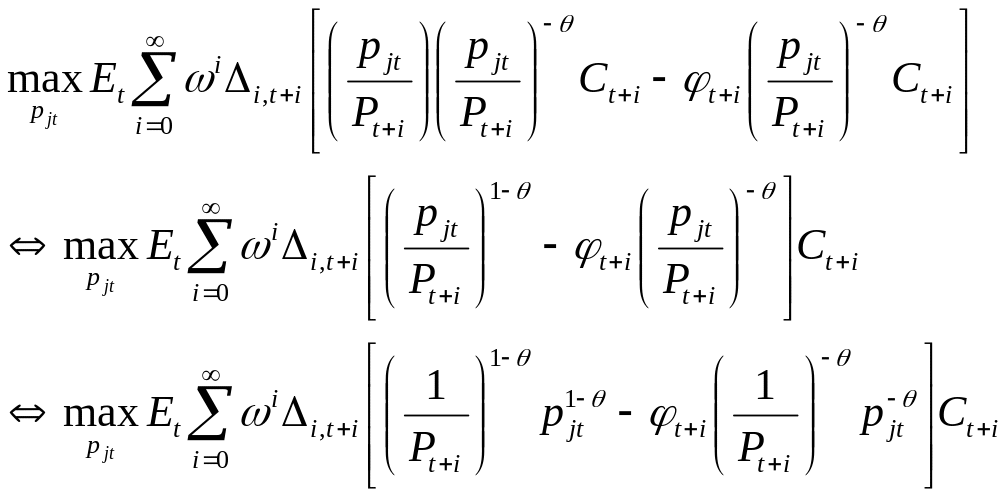
(26)

Более того, все фирмы имеют одну и ту же технологию производства и имеют идентичные функции спроса (с постоянной и одинаковой эластичностью спроса по цене). Другими словами, фирмы идентичны, за исключением того, что они, возможно, установили текущие цены в различные периоды в прошлом. Однако все фирмы, пересматривающие свои цены в периоде , сталкиваются с одной и той же оптимизационной проблемой, поэтому все приспосабливающиеся в периоде фирмы установят одну и ту же цену. Обозначая оптимальные цены = данных фирм, вычислим условие первого порядка (FOC):

(27)

Используя и преобразовывая, получаем:

(28)

Это и есть оптимальное правило ценообразования в условиях жесткости цен (используя предпосылку Кальво).