31 Основи термодинаміки і кінетичної теорії газів (рівноважний тиск металевої пари).

Перехід твердого тіла або рідини в газоподібний стан можна описати як з макроскопічної, так і мікроскопічної точки зору. У першому випадку використовується термодинамічний підхід, і розглядаються такі кількісні характеристики, як швидкість випаровування, взаємодія між атомами речовини, яка випаровується, і випарника та ін. У другому випадку опис базується на кінетичній теорії газів, яка, між іншим, застосовується також при розгляді процесу відкачування газів із вакуумної камери. Рівноважний тиск пари. При термодинамічному підході конденсований або газоподібний стан речовини є функцією таких параметрів, як тиск, температура, об'єм і маса. Особливе значення має умова термодинамічної рівноваги (кількість атомів, які залишають тверде тіло чи рідину, дорівнює кількості атомів, які конденсуються знову). Всі речовини мають певне значення тиску насиченої пари (рн), який залежить від температури. Тиск насиченої пари над поверхнею сконденсованої фази є важливою характеристикою, яка дозволяє оцінити можливості випаровування речовини і ті температури, при яких досягаться необхідна швидкість випаровування і навіть конденсації. Залежність як відомо, дуже добре описується рівнянням Клапейрона-Клаузіуса. Для цього розглянемо умову фазової рівноваги насичена пара - тверде тіло і поняття про термодинамічний потенціал Гіббса (Ф). Із теорії фазової рівноваги відомо, що при незмінних зовшшньому тиску та температурі дві фази будуть в рівновазі, якщо виконується умова де U-внутрішня енергія; S-ентропія; індекси п та к поз-начають пару і конденсовану фазу (в нашому ви-падку - тверде тіло або рідину). Переходячи від інтегрального співвідношення запишемо або де повний диференціал термодинамічного потенціалу Гіббса. Тоді

Потім . Враховуючи, що при , одержимо якщо скористаємося рівнянням для одного моля ідеального газу . Після потенціювання одержуємо залежність тиску насиченої пари від температури: яка підтверджується експериментально це ілюструється на прикладі насиченої пари алюмінію).

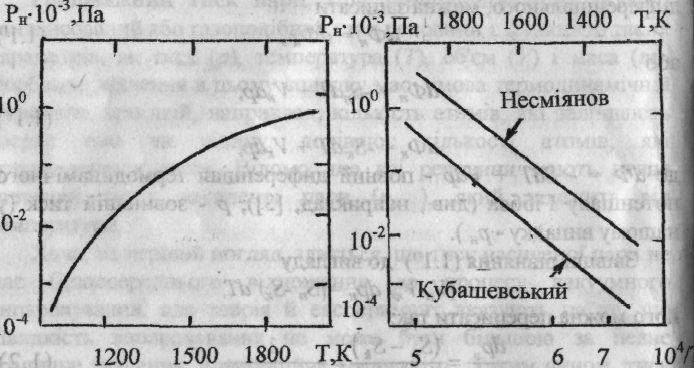
за кутовим коефіцієнтом залежності можна визначити величину За даними О.Кубашевського та О.М.Несміянова (рис.) вона дорівнює відповідно 313 та 305 Дж/моль, що відрізняється не суттєво, хоча абсолютні значення одержані цими авторами, різні.

32 Основи термодинаміки і кінетичної теорії газів (розподіл атомів металевої пари за швидк).

Д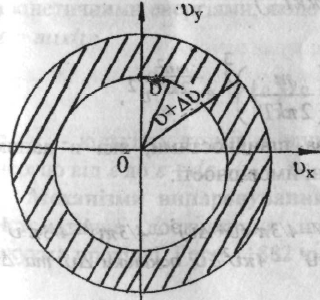 ля того щоб одержати функцію розподілу атомів (молекул) речовини, яка випаровується, за швидкостями, необхідно провести такі ж міркування, як і для газових молекул при одержанні розподілу Максвелла. Якщо позначити кількість атомів із одиниці об'єму пари металу, які мають швидкість від через то можна записати де - поки що невідома функція; п - концентрація атомів; елемент об'єму в просторі швидкостей, який займають атоми зі швидкістю від . Для знаходження об'єму необхідно розглянути в просторі швидкостей кульовий прошарок із внутрішнім радиусом і зовнішнім

Із геометрії рисунка випливає, що Підставивши і ввівши коефіцієнт пропорційності в запишемо Функция знахо-диться методами статистичної фізики, і в кінцевому вигляді її можна записати так: де к - постійна Больцмана; m - маса атома.

Ймовірність того, що атом із металевої пари буде мати швидкість в інтервалі , можна записати так: Знаходиться явний вигляд коефіцієнта пропорційності: У кінцевому вигляді розподіл Максвелла можна записати або де - функція розподілу за швидкостями. 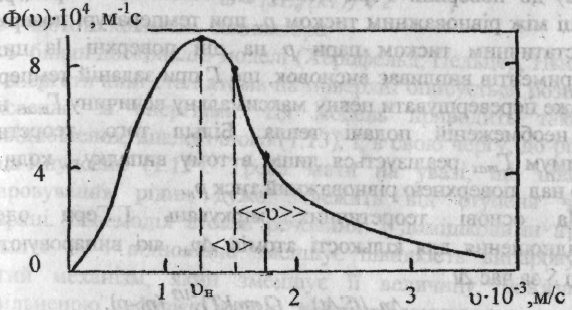Розподіл Максвелла для атомів алюмінію при найбільш ймовірна; середня та - середня квадратична швидкості) середньої та середньоквадратичної швидкостей. Ці швидкості співвідносяться між собою так: Від розподілу за швидкостями можна перейти до розподілу за кінетичними енергіями, якщо підставити та де - кількість атомів в одиниці об'єму, які мають кінетичну енергію від