- •60Путей сообщения (миит)
- •Математические модели и методы в инженерных расчетах
- •Введение
- •1.Математические модели
- •1.1Модель процесса проектирования
- •1.2Теория вероятностей
- •1.3 Математическая статистика
- •1.4Сортировка
- •1.5Интерполяция табличных зависимостей
- •1.6Аппроксимация.
- •1.6.1Метод наименьших квадратов для многочленов
- •1.6.2 Полиномиальная аппроксимация
- •1.6.3Линейная аппроксимация
- •1.7Сглаживание данных
- •1.8Предсказание (экстраполяция функции)
- •1.9 Рис. 1.14 Экстраполяция функции. Численное дифференцирование
- •1.10Вычисление определенного интеграла
- •1.11Численное решение дифференциальных уравнений
- •1.12Моделирование рельефа местности
- •1.13 Рис. 1.19 Цифровая модель рельефа и продольный профиль земли по заданному направлению Моделирование продольного профиля и плана при реконструкции железных дорог
- •2.Математические методы
- •2.1Реализация численной модели на эвм
- •2.2Целевая функция. Ограничения
- •2.3Оптимизация без ограничений
- •2.3.1Прямой одномерный поиск
- •2.4Прямой многомерный поиск
- •2.4.1Градиентные методы
- •2.5 Рис. 2.35 Градиентный метод. Оптимизация с ограничениями.
- •2.6Линейное программирование
- •2.7Нелинейное программирование
- •2.8Графы
- •2.9Метод динамического программирования.
- •2.10Поиск кратчайшего пути в графе
- •2.11Экономические аспекты автоматизированного проектирования.
- •2.12Проблемы программных реализаций.
- •Программного обеспечения.
- •1. Математические модели 4
- •2. Математические методы 41
- •Екатерина Александровна Рыжик
1.11Численное решение дифференциальных уравнений
Дифференциальное
уравнение первого порядка:
![]() ,
где y
- неизвестная функция от x.
Обычно считается, что это уравнение
разрешимо относительно производной,
т.е. имеет вид:
,
где y
- неизвестная функция от x.
Обычно считается, что это уравнение
разрешимо относительно производной,
т.е. имеет вид:
![]() .
Для решения уравнения необходимо задание
начальных условий: x
= x0
и y
= y0.
.
Для решения уравнения необходимо задание
начальных условий: x
= x0
и y
= y0.
Примером
дифференциального уравнения первого
порядка является основное уравнение
движения поезда:
![]() ,
где r(t)
- удельная
равнодействующая сила.
,
где r(t)
- удельная
равнодействующая сила.
Если уравнение
имеет вид
и заданы начальные условия x
= x0
и y
= y0,
то, подставляя значения x0
и y0
в функцию
![]() ,
мы найдем величину производной в точке
x0:
,
мы найдем величину производной в точке
x0:
![]() .
.
Значение функции:
![]() ,
где x
- малое приращение x.
,
где x
- малое приращение x.
Отсюда значение
функции y1
= y
(x1)
=
![]() ,
,
где x1 = x0 + x.
Теперь, принимая
точку (x1,y1)
за исходную, можно точно таким же образом
получить точку y2
= y
(x2)
=
![]() ,
где x2
= x1
+ x.
Таким образом, шаг за шагом, можно
последовательно вычислять значения
функции для различных x.
Это - метод
Эйлера.
,
где x2
= x1
+ x.
Таким образом, шаг за шагом, можно
последовательно вычислять значения
функции для различных x.
Это - метод
Эйлера.
Рис. 1.16
Метод Эйлера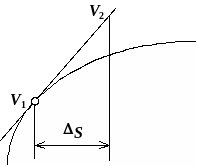
![]() остается постоянной на интервале x
и равна величине, рассчитанной в начале
данного интервала. Пользуясь этим
методом, получают не точные, а приближенные
значения функции y
в связи с тем, что производная
изменяется на интервале x.
Пользуясь этим методом, мы допускаем
ошибку в определении y,
причем тем большую, чем больше x.
остается постоянной на интервале x
и равна величине, рассчитанной в начале
данного интервала. Пользуясь этим
методом, получают не точные, а приближенные
значения функции y
в связи с тем, что производная
изменяется на интервале x.
Пользуясь этим методом, мы допускаем
ошибку в определении y,
причем тем большую, чем больше x.
Геометрический смысл рассматриваемого метода состоит в том, что в каждой точке, последовательно, приращение y рассчитывается по касательной в начальной точке каждого интервала (рис. 1.16). При этом ошибка последовательно накапливается и рассчитанные значения y все более и более «отстают» от действительных или «перегоняют» их.
Более точное
решение можно получить, если последовательно
принимать значения,
![]() ,
полученные по формуле Эйлера, за первое
приближение. Для получения более точного
второго приближения будем брать среднее
арифметическое производной в начале и
конце интервала, вычисляя производную
в его конце при помощи первого приближения
,
полученные по формуле Эйлера, за первое
приближение. Для получения более точного
второго приближения будем брать среднее
арифметическое производной в начале и
конце интервала, вычисляя производную
в его конце при помощи первого приближения
![]() .
Таким образом,
.
Таким образом,
![]() .
.
При необходимости можно найти следующее (ие) приближение (я).
Такую схему вычислений называют схемой с пересчетом, потому что величина на каждом шаге пересчитывается, заменяется более надежной величиной.
При решении
дифференциальных уравнений требуется
найти на отрезке [a,b]
функцию, удовлетворяющую уравнению
![]() и начальному условию
и начальному условию
![]() .
Численное решение заключается в отыскании
способа вычисления приближенного
значения функции
.
Численное решение заключается в отыскании
способа вычисления приближенного
значения функции
![]() для любого значения аргумента
для любого значения аргумента
![]() .
.
В тяговых расчетах
решается дифференциальное уравнение
движения поезда:
![]() .
.
Необходимо построить кривую скорости на участке (интервале) [a,b].
Разобьем интервал [a,b] на n равных частей. Будем считать, что величина равнодействующей на каждом из полученных отрезков постоянна rk = const. При трогании поезда со станции его скорость равна 0, т.е. при S=0 - V=0.
Формула метода
Эйлера для получения нового значения
скорости на элементарном отрезке DS:
![]()
При решении уравнения движения поезда, обычно, исходят из преобразованного уравнения движения поезда, при условии постоянства равнодействующей на отрезке DS.
![]() .
Внеся V
под знак дифференциала, получим:
.
Внеся V
под знак дифференциала, получим:
![]()
Применяя формулу метода Эйлера, будем иметь:
![]() .
.
Рис. 1.17
Построение кривой скорости методом
Эйлера и методом с возвратами