
- •60Путей сообщения (миит)
- •Математические модели и методы в инженерных расчетах
- •Введение
- •1.Математические модели
- •1.1Модель процесса проектирования
- •1.2Теория вероятностей
- •1.3 Математическая статистика
- •1.4Сортировка
- •1.5Интерполяция табличных зависимостей
- •1.6Аппроксимация.
- •1.6.1Метод наименьших квадратов для многочленов
- •1.6.2 Полиномиальная аппроксимация
- •1.6.3Линейная аппроксимация
- •1.7Сглаживание данных
- •1.8Предсказание (экстраполяция функции)
- •1.9 Рис. 1.14 Экстраполяция функции. Численное дифференцирование
- •1.10Вычисление определенного интеграла
- •1.11Численное решение дифференциальных уравнений
- •1.12Моделирование рельефа местности
- •1.13 Рис. 1.19 Цифровая модель рельефа и продольный профиль земли по заданному направлению Моделирование продольного профиля и плана при реконструкции железных дорог
- •2.Математические методы
- •2.1Реализация численной модели на эвм
- •2.2Целевая функция. Ограничения
- •2.3Оптимизация без ограничений
- •2.3.1Прямой одномерный поиск
- •2.4Прямой многомерный поиск
- •2.4.1Градиентные методы
- •2.5 Рис. 2.35 Градиентный метод. Оптимизация с ограничениями.
- •2.6Линейное программирование
- •2.7Нелинейное программирование
- •2.8Графы
- •2.9Метод динамического программирования.
- •2.10Поиск кратчайшего пути в графе
- •2.11Экономические аспекты автоматизированного проектирования.
- •2.12Проблемы программных реализаций.
- •Программного обеспечения.
- •1. Математические модели 4
- •2. Математические методы 41
- •Екатерина Александровна Рыжик
1.3 Математическая статистика
Задачи математической статистики состоят в том, чтобы на основании знания некотором свойств подмножества, взятых из некоторого их множества, сделать какие-нибудь утверждения о свойствах этого множества, называемого генеральной совокупностью. В генеральной совокупности нас обычно интересует некоторый признак, который обусловлен случайностью и может иметь качественный или количественный характер.
Интересующий нас параметр некоторой генеральной совокупности может быть представлен в математической модели некоторой случайной величиной Х.
Под случайной выборкой объема n понимается выбор n объектов из генеральной совокупности, причем выбор отдельных объектов производится независимо один от другого. Результатом случайной выборки объема n является совокупность (х1,.,хn) значений признака.
Гистограмма и эмпирическая функция распределения
Пусть имеется выборка (х1,....,хn) - таблица наблюденных значений - из генеральной совокупности с признаком Х.
Для того чтобы получить первое представление об этом распределении составляют гистограмму (рис.1.6). Производят разбиение оси на определенное число граничащих друг с другом интервалов 1,...,k. Затем подсчитывают число mi выборочных значений, лежащих в i (1 i k). Эти числа называют групповыми частотами. Над i рисуют прямоугольники высоты mi/n (относительные частоты попадания в интервал). Полученный ступенчатый график называют гистограммой выборки.
Рис. 1.6
Гистограмма.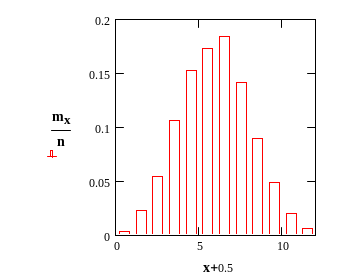
![]() .
Ступенчатая функция
.
Ступенчатая функция
![]() называется эмпирической функцией
распределения выборки (х1,...,xn)
(рис. 1.7).
называется эмпирической функцией
распределения выборки (х1,...,xn)
(рис. 1.7).
Рис. 1.7
Эмпирическая кривая распределения.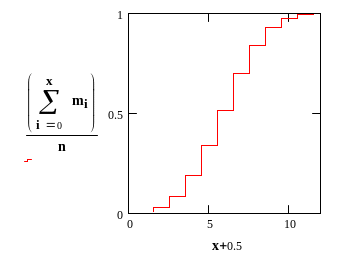
Функции выборки:
среднее
значение (математическое ожидание)
![]() ;
дисперсия
;
дисперсия
![]() ;
разброс (среднее квадратичное отклонение)
;
разброс (среднее квадратичное отклонение)
![]() .
.
Не существует общего критерия, который позволял бы решить, когда выборка может считаться большой, а когда малой. В то время как распределение одной функции выборки уже при n=30 может считаться очень хорошим приближением, для другой - и при n=100 это еще невозможно.
Для проверки соответствия наблюдений какому-либо закону, выдвигают гипотезу. Например, анализ гистограммы показанной на рис.1.6 позволяет выдвинуть гипотезу о том, что анализируемая случайная величина имеет нормальное распределение (рис. 1.8).
Для данной выборки
среднее значение
![]() =
5,928, разброс
= 2,092.
=
5,928, разброс
= 2,092.
Для проверки гипотезы используются критерии согласия.
Рис. 1.8
Гистограмма и гипотетическая кривая
плотности нормального распределения.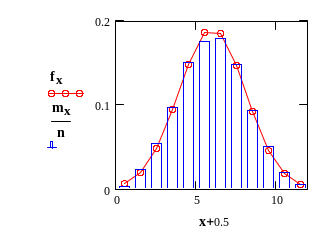
![]() ,
где pi
- ожидаемая
(теоретическая) вероятность попадания
случайной величины в i-й
интервал; mi
- фактическая частота попадания в
выделенные n
интервалов. Критерием служит соотношение
расчетной величины 2
и ее максимального значения
,
где pi
- ожидаемая
(теоретическая) вероятность попадания
случайной величины в i-й
интервал; mi
- фактическая частота попадания в
выделенные n
интервалов. Критерием служит соотношение
расчетной величины 2
и ее максимального значения
![]() ,
определяемого по таблицам или расчетом,
где
- уровень значимости,
определяющий надежность оценки. Если
2
,
определяемого по таблицам или расчетом,
где
- уровень значимости,
определяющий надежность оценки. Если
2
![]() ,
гипотеза принимается.
,
гипотеза принимается.
Для рассматриваемого примера получено значение критерия согласия (MathCAD) равное 0,988. Вероятность отсутствия ошибки при принятии гипотезы мала, т.е. с вероятностью близкой к 1, можно считать распределение нормальным.
Другая
задача, которая очень часто возникает,
связана с назначением доверительных
интервалов для среднего значения, т.е.,
что данное среднее значение с заданным
уровнем доверия (доверительной
вероятности)
![]() равно
равно
![]() .
.
Зададимся
несколькими уровнями доверия, например,
90%, 95% и 99%. Доверительного интервалы,
обычно вычисляют на основании критерия
Стьюдента. Величина доверительного
интервала
![]() ,
где n
- количество измерений случайной
величины; p0
- доверительная вероятность;
,
где n
- количество измерений случайной
величины; p0
- доверительная вероятность;
![]() -
коэффициент Стьюдента, принимаемый по
таблицам или рассчитываемый;
-
оценка среднеквадратичного отклонения.
-
коэффициент Стьюдента, принимаемый по
таблицам или рассчитываемый;
-
оценка среднеквадратичного отклонения.
В результате вычислений для рассматриваемого примера были получены значения доверительных интервалов:
Доверительная вероятность |
90% |
95% |
99% |
Способы |
5,928±0,144 |
5,928±0,185 |
5,928±0,262 |
Представления |
5,784¸6,072 |
5,743¸6,213 |
5,666¸6,190 |
Для определения количества экспериментов, обеспечивающих получение статистических зависимостей с требуемым уровнем доверия и величиной доверительного интервала, рассчитаем таблицу значений величины множителя, на который умножается оценка среднеквадратического отклонения при определении доверительного интервала:
Количество величин |
Доверительная вероятность |
||
в доверительном интервале |
0,95 |
0,99 |
0,995 |
3 |
3 |
4 |
5 |
1,5 |
4 |
7 |
8 |
1 |
7 |
10 |
12 |
0,5 |
20 |
30 |
35 |
0,25 |
60 |
100 |
135 |
0,1 |
400 |
700 |
795 |
Как видно из таблицы уже при количестве опытов 20-35, величина доверительного интервала достигает половины величины среднеквадратичного отклонения , что вполне приемлемо для большинства технических приложений.
