12. Умови монотонності функції. Означення екстремума функції, необхідні і достатні умови існування локального екстремума. Напрям опуклості графіка функції та точки перегину.

Умови монотонності функції

Позначимо . Припустимо, що точка с - внутрішня точка D(f).

def. зростає в т

Аналогічно дається означення спадної функції в точці.

def. монотонна в точці зростає або спадає в точці .

Теорема (достатня умова монотонності функції в точці)

диференційована в т. c та , то ( ) в т. с.

Теорема 5.12 (критерій нестрогої монотонності функції на інтервалі). Якщо – диференційована на , то для того, щоб функція була неспадною (незростаючою) на цьому інтервалі необхідно і достатньо, щоб похідна у всіх точках інтервалу була невід’ємною (недодатною), тобто .

Доведення. Достатність. Нехай , , а для визначеності припустимо, що . Оскільки диференційована на інтервалі то вона диференційовна на відрізку , що лежить в середині цього інтервалу, тоді неперервна на .

Отже, вимоги теореми Лагранжа здійснюються на відрізку , тому можна знайти точку таку, що .

Якщо на , а за припущенням , тоді , тобто . Таким чином , – не спадна.

Необхідність:

Дано: диф. на , не спадна.

Довести:

Пп:, тоді із теореми про достатню умову монотонності функції в точці, маємо, що в т. с спадає, що суперечить умові. ■

Теорема (достатня умова строгої монотонності функції на інтервалі)

диференційовна на та , то ( ) на .

Доведення дублює обґрунтування достатності попередньої теореми.

Означення екстремума функції, необхідні і достатні умови існування локального екстремума.

def.. Точка - точка локального максимуму функції

1) точка - внутрішня точка ;

2) .

Аналогічно дається означення локального мінімуму функції.

def.. Точка - точка локального екстремуму функції в точці с функція має локальний максимум або локальний мінімум.

Теорема Ферма (необхідна умова локального екстремуму).

диференційована в т. c та т. с точка локального екстремуму, то

Доведення. . – диференційована в т с .

Оскільки т. с – точка локального екстремуму, то в цій точці функція не може спадати, а тому її похідна в цій точці не може бути меншою за нуль, вона також не може зростати, тому похідна не може бути більшою за нуль, Отже, . ■

Теорема (перша достатня умова loc extr)

Доведення. І) Нехай - довільна точка проколотого -околу. Оскільки функція диференційовна в , то вона диф. на пів відрізку , а тому і непер. на ньому. Крім того, функція неперервна в точці с. Тому можна застосувати на цьому відрізку теорему Лагранжа: , де ξ лежить поміж х і с.

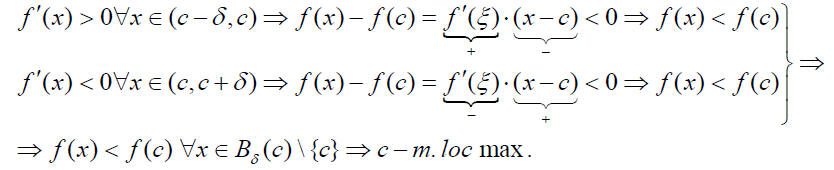
ІІ) доведення аналогічне І)

ІІІ) Нехай для визначеності в усіх точках із є додатнім, тоді

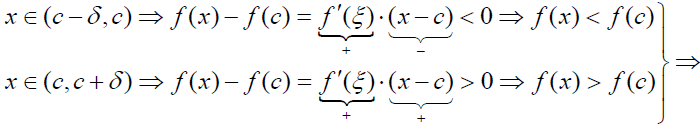
в с точці немає loc extr. ■

Теорема 5.15 (друга достатня умова loc extr)

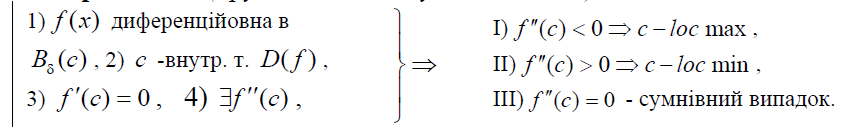
Доведення.

І)

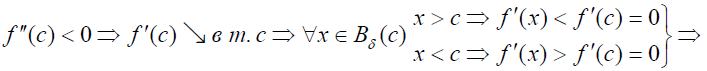
за попередньою теоремою т. с – т. loc max

ІІ) Доводиться аналогічно.

ІІІ) Функція в точці 0 зростає і, відповідно, не має екстремуму, хоч , а в т. 0 має лок. мінімум, а .Тому цей випадок є сумнівним.

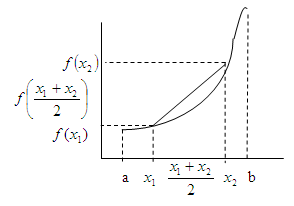Напрям опуклості графіка функції та точки перегину.

def. наз. опуклою вниз на , якщо

,

Частковий випадок:

Геометрично ця нерівність означає, що точка на січній з координатами – що відповідає середині січної, лежить вище за точку з координатами , що відповідає точці на графіку абсциса, якої є серединою відрізку .

Критерії опуклості вниз

1. – диференційована на – опукла вниз на , тоді і тільки тоді коли зростає не строго.

2. – двічі диференційована на – опукла вниз на , тоді і тільки тоді коли .

Для опуклої вгору аналогічно.