Второй замечательный предел

Следствия

6. Означення неперервності функції в точці. Неперервність елементарних функцій. Локальні властивості неперервної функції. Точки розриву

Неперервність функції в точці

Означення. Функція називаеться неперервною в точці а, якщо . Функції називаеться неперервною справа(зліва) в точці а, якщо .

Теорема . Якщо функції неперервні в точці а, то функції також неперервні в точці а.

Нехай функшя задана на множині X, i У - множина значень цієї функції. Нехай на множині У задана функшя кажуть, що на множит X задана композиція функції(складна функція .

Класифікація точок розриву.

Нехай а - гранична точка области визначення функції f(x). Точка а називаеться точкою розриву функції f(x) , якщо f(x) в цій точці не е неперервною. Тод1 а називаеться:

1. точкою усувного розриву, якщо існує

2. точкою розриву I роду, якщо існують

3. точкою розриву II роду, якщо в точці а не юнуе хоча б одна з одностороншх границь.

(під словами існує(не існує) мається на вазі існує(не існує) скінчена границя).

Неперервність елементарних функцій

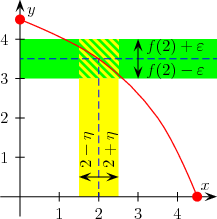
Приклад неперервної функції

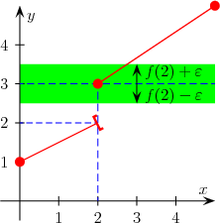
Приклад розривної функції в точці x=2. Функція не є неперервною зліва точки x=2

проте є неперервною справа:

Функція дійсної змінної, яка означена в області , неперервна в точці якщо для довільного знайдеться таке , що з випливає . Функція неперервна в області , якщо неперервна в кожній точці цієї області.

Нехай — гранична точка множини A.

Означення неперервності в точці

Функція f називається неперервною в точці якщо:

1. функція визначена в точці .

2. існує границя

3.

Означення неперервності в точці за Коші

Функція f називається неперервною в точці якщо:

Означення неперервності в точці за Гейне

Функція f називається неперервною в точці якщо: , якщо

Точки розриву

Точка розриву - це така точка (значення аргументу) в якій функція не є неперервною. Розрізняють такі види точок розриву:

Розрив називають усувним, якщо в даній точці існує границя функції, що не збігається з значенням функції.

Точку називають точкою розриву першого роду, якщо існують скінченні ліва та права границі в даній точці, та вони не збігаються.

Якщо хоча б одна одностороння границя не існує, чи нескінченна, то точку називають точкою розриву другого роду.

Локальні Властивості неперервної функції

Локальні властивості:

• Функція, безперервна в точці a, є обмеженою в деякій околиці цієї точки.

• Якщо функція f неперервна в точці a і для всіх x, Досить близьких до a.

• Якщо функції f i g безперервні в точці a, То функції теж неперервні в точці a.

• Якщо функції f i g безперервні в точці a і при цьому , То функція теж неперервна в точці a.

• Якщо функція f неперервна в точці a і функція g неперервна в точці , То їх композиція неперервна в точці a.

9 Диф-ть ф-и одной пер-й.

Пусть дана ф-я , опред. на . Выберем любую т. и дадим нек. приращ. (настолько малое, что ) Приращ. ф-и в т. :

Опр. Производной ф-ей от наз. предел отношения приращения ф-и к приращ. ее аргумента, когда последн.

Опр. наз. дифференцируемой в т. , если

A=const, не зависящ. от , - бмф при

Th.

Утв: , т. е. если слева = справа

Опр. Лин. часть приращ. ф-и наз. диф-лом ф-и

Th. , , , то :

Th.

Th. : , монот, , , тогда , , монот.,

.

Опр. наз. возраст. в т. если сущ. нек окр-ть этой т. в кот.

.

Опр. наз. убыв. в т. если сущ. нек окр-ть этой т. в кот.

.

Замечание: 1 Если ф-я возраст. (убыв.), то она возраст (убыв.) в т. .

2. Если ф-я возраст. (убыв.) в т. , то она не обяз. возраст (убыв).

Th1. возр. (убыв.) в т.

Необх. усл-я экстремума.

Опр. Ф-я имеет в т. loc max (min), если в нек проколотой окр-ти этой т. вып-ся ( )

Опр. Ф-я имеет loc экстремум в т. , если в этой т. она имеет или loc min или loc max.

Th (Ферма): , - loc extr. .

Док-во: По усл.

Т.к. имеет в т. loc extr, то она не может в этой точке ни возр. ни убыв, тогда по th1 не м. б. >0 или <0, .

Th Ролля: , :

Док-во: (th Вейерштрасса) ,

1)

2) , что или (т.к. ) (th Ферма)

Th Лагранжа: : .

Док-во: введем

(th Ролля)

(разность и лин. ф-и)

Сл-я:

Th1(дост. усл-я постоянства ф-и)

,

Th2(усл-я монотонности)

неубыв. на

невозр. на

Th3(дост. усл-я строгой монотонности)

возр. на

убыв. на

Th Коши

:

Док-во а) П. п. (th Ролля) :

б)

(th Ролля)

Th Дарбу и для нек-х .

Тогда :

10. Теорема Коші про відношення приростів двох функцій, диференційованих на відрізку. Поняття неозначеності в теорії границь. Теореми Лопіталя та їх застосування до розкриття неозначеності.

Теорема Коші. Якщо і − непер. на

і − диф. на

Доведення.

Розглянемо допоміжну функцію −непер. на функція, диф. на

за теоремою Ролля

, .

П равило Лопіталя 1 .

Нехай і − диф. на множині

, тобто під знаком має місце невизначеність

якщо скінченна або нескінченна

Доведення.

і − диф. в непер. в

і в т. мають усувний розрив.

Довизначаємо обидві функції в точці . Тоді і − непер. в .

Нехай ,

розглянемо − на цьому відрізку обидві функції і − непер, а на функції і − диф. .

Тоді за теоремо Коші .

або .

Існує за умовою для за Гейне .

П равило Лопіталя 2 .

Нехай і − диф. на множині

− скінченна або нескінченна

Доведення.

Розглянемо , .

, .

або

Відомо −фікс. .

Д ля

.

.

Висновок: , за Гейне це означає .