
- •Множини, їх види, операції над множинами та їх властивості. Числові множини. Точна верхня і точна нижні межі множин
- •2. Множина раціональних чисел та її властивості. Потужність множини раціональних чисел.
- •3. Множина дійсних чисел та її властивості. Арифметичні операції над дійсними числами. Упорядкування дійсних чисел
- •– Дистрибутивність.
- •4. Числові послідовності, їх види та арифметичні операції над ними. Граничні точки, границя, нижня і верхня границі послідовності та умови їх існування.
- •5.Поняття функції. Способи завдання функції та їх класифікація. Границя функції в точці за Гейне і за Коші та їх еквівалентність. Істотні границі
- •Второй замечательный предел
- •6. Означення неперервності функції в точці. Неперервність елементарних функцій. Локальні властивості неперервної функції. Точки розриву
- •Означення неперервності в точці
- •Означення неперервності в точці за Коші
- •Точки розриву
- •Локальні властивості:
- •11. Формула Тейлора диференнційовної функції та її залишковий член. Формула Тейлора для елементарних функцій та її застосування.
- •Ряд Тейлора
- •Разложение в ряд Тейлора (Маклорена) основных элементарных функций.
- •12. Умови монотонності функції. Означення екстремума функції, необхідні і достатні умови існування локального екстремума. Напрям опуклості графіка функції та точки перегину.
- •13. Поняття первісної функції, невизначеного інтегралу та їх властивості. Основні методи інтегрування (заміна змінної інтегрування, інтегрування частинами а інші).
- •2) Теорема (Інтегрування частинами)
- •14. Означений інтеграл та його властивості. Необхідні та достатні умови інтегрованості за Ріманом. Класи інтегрованих функцій. Формула Ньютона – Лейбніца.
- •19. Дослідження на локальний і тотальний екстремум функції багатьох змінних. Поняття про умовний екстремум.
- •20 Численные ряды, признаки их сх-ти. Абсолютно и условно сх-ся ряды,их св-ва
- •Числовые ряды с положительными членами: , - числовой ряд с положительными членами.
- •Властивості:
- •22. Степеневі ряди. Теорема Абеля про область збіжності степеневого ряду. Формула Коші-Адамара для визначення радіуса збіжності. Рівномірна збіжність, диференціювання і інтегрування степеневих рядів.
- •23.Функциональные последовательности и ряды.
- •2.Почленное дифференцирование
- •24. Тригонометрический ряд фурье
- •25. Кратні інтеграли (подвійні, потрійні): означення властивості, обчислення, застосування.
- •26. Скалярне та векторне поле та їх характеристики (градієнт скалярного поля, дивергенція і ротор векторного поля та ін.). Формули Грина, Остроградського-Гауса та Стокса.
- •27. Поняття функції комплексної змінної . Границя, неперервність, похідна фунції комплексної змінної. Умови Коши-Рімана диференційованості функції.
- •28. Елементарні функції комплексної змінної. Означення інтегрального лишку та його обчислення. Основна теорема про лишки та її застосування.
- •Твердження
- •Доведення
- •31. Метрические пространства. Определение и примеры метрических пространств. Сходимость последовательностей элементов метрических пространств.
- •32. Принцип сжимающих отображений.
- •33. Мера лебега в конечном евклидовом пространстве.
- •34. Интеграл лебега.
- •35. Скалярное, векторное и смешаное произведение векторов.
- •36. Прямая на плосости. Уравнение прямой на пл-ти в прямоугольной декартовой системе координат.
- •39. Элипс, парабола, гипербола и их свойства.
- •40. Приведение линии 2-го порядка к каноническому виду
Твердження
Нехай
U
—
відкрита,
однозв'язна
підмножина
комплексної
площини
![]() ,
z1,...,zn
множина
особливаих точок у
U
і
f
—
функція
що
є голоморфною у множині
U
-
{z1,...,zn}.
Якщо γ —
деяка замкнута
спрямлювана
крива
у
U,
якій не належать
zk.
Тоді :
,
z1,...,zn
множина
особливаих точок у
U
і
f
—
функція
що
є голоморфною у множині
U
-
{z1,...,zn}.
Якщо γ —
деяка замкнута
спрямлювана
крива
у
U,
якій не належать
zk.
Тоді :
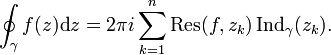
В даній рівності,
Res(f,zk)
позначає лишок
функції
f
в точці
zk,
а
![]() індекс
контура
γ відносно
точки zk.
індекс
контура
γ відносно
точки zk.
Дане число може бути визначене за формулою:
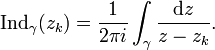
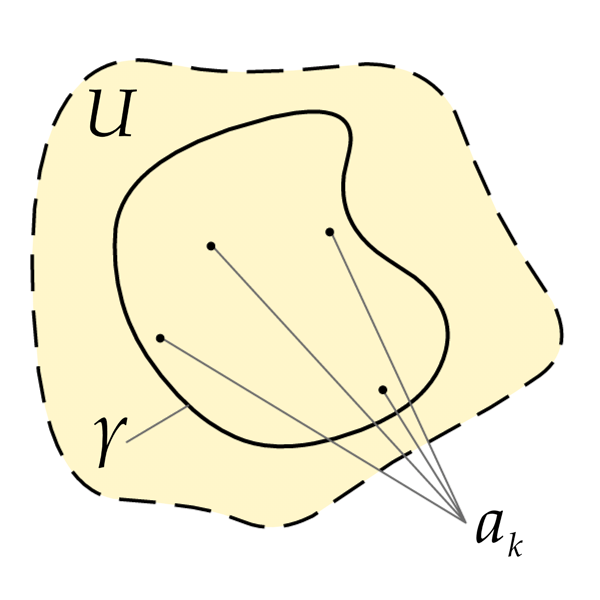
Замітка.
У найпоширенішому випадку крива
вважається жордановою, тобто вона ніде
не перетинається сама з собою. В такому
випадку крива розбиває область
U
на дві частини
внутрішню та зовнішню. Для внутрішніх
особливих точок (як на малюнку) в таких
випадках
![]() ,
для зовнішніх
,
для зовнішніх
![]() і їх можна не
враховувати. Тоді рівність із твердження
теореми перепишеться:
і їх можна не
враховувати. Тоді рівність із твердження
теореми перепишеться:
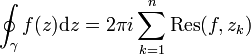
де сума береться по всіх внутрішніх особливих точках.
Доведення
Нехай
F
— множина
особливих точок функції
f,
і для
![]() ,
функція допускає розклад у
ряд
Лорана
в деякому
проколотому диску
,
функція допускає розклад у
ряд
Лорана
в деякому
проколотому диску
![]() радіуса
радіуса
![]() з центром у
точці
з центром у
точці
![]() :
:
![]()
Нехай
![]() ряд, визначений
із сингулярної частини ряду Лорана :
ряд, визначений
із сингулярної частини ряду Лорана :
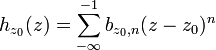
Він є нормально
збіжним на
компактних
підмножинах
![]() .
.
Визначимо функцію g у всій множині U як:
![]()
Дана функція є голоморфною в усій області U і тому згідно з інтегральною теоремою Коші:
![]()
згідно з визначенням функції g :
![]()
Зважаючи на
нормальну збіжність
![]() можна записати
:
можна записати
:
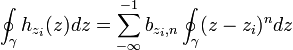
Обчислюючи інтеграли одержуємо:
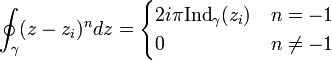
Об'єднавши дві попередні формули можна одержати:
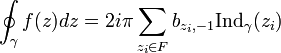
і згадавши визначення лишка одержуємо необхідний результат:
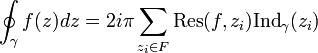
31. Метрические пространства. Определение и примеры метрических пространств. Сходимость последовательностей элементов метрических пространств.
![]() Множество
называется метрическим пространством,
если
Множество
называется метрическим пространством,
если
![]() определено неотрицательное число
определено неотрицательное число
![]() ,
называемое расстоянием между элементами
и
,
называемое расстоянием между элементами
и
![]() и удовлетворяющее 3 аксиомам:
и удовлетворяющее 3 аксиомам:
1. аксиома выбора:
![]()
2. аксиома симметрии:
![]()
3. аксиома
треугольника:
![]()
Если на множестве
![]() задана функция
удовлетворяющая 3 аксиомам из
,
то эта функция называется метрикой
заданной на
.
задана функция
удовлетворяющая 3 аксиомам из
,
то эта функция называется метрикой
заданной на
.
Если на множестве
задана метрика
![]() ,
то полученное таким образом метрическое
пространство принято обозначать
или
,
то полученное таким образом метрическое
пространство принято обозначать
или
![]() ,
в зависимости от того нужно ли указывать
каким образом задана метрика.
,
в зависимости от того нужно ли указывать
каким образом задана метрика.
Элементы метрического пространства принято называть точками этого пространства.
Примеры метрических пространств:
1. На множестве всех упорядоченных совокупностей действительных чисел зададим следующим образом
![]() -
мерное Евклидово пространство
-
мерное Евклидово пространство
2. На множестве всех ограниченных числовых последовательностей зададим следующим образом
![]() - пространство
ограниченных числовых последовательностей
- пространство
ограниченных числовых последовательностей
3. Пусть
![]() фиксированное
число
фиксированное
число
![]() ,
на множестве всех числовых последовательностей
,
на множестве всех числовых последовательностей
![]() ,
каждая из которых удовлетворяет условию
сходимости числового ряда
,
каждая из которых удовлетворяет условию
сходимости числового ряда
![]() ,
зададим
следующим образом
,
зададим
следующим образом
![]() - пространство
числовых последовательностей суммируемых
со степенью
- пространство
числовых последовательностей суммируемых
со степенью
4. На множестве всех числовых последовательностей зададим следующим образом
![]() -
пространство числовых последовательностей
-
пространство числовых последовательностей
5. На множестве
всех действительных функций определенных
и непрерывных на
![]() зададим
следующим образом
зададим
следующим образом
![]() .
Полученное таким образом пространство
обозначается символом
.
Полученное таким образом пространство
обозначается символом
![]() и называется пространством функций
непрерывных на
и называется пространством функций
непрерывных на
![]() .
.
6. На множестве
всех определенных на
и
![]() раз
непрерывно дифференцируемых функций
зададим
следующим образом
раз
непрерывно дифференцируемых функций
зададим
следующим образом
![]() ,
где
,
где
![]() производная.
Полученное таким образом пространство
обозначается символом
производная.
Полученное таким образом пространство
обозначается символом
![]() и называется пространством
раз
непрерывно дифференцируемых на
функций.
и называется пространством
раз
непрерывно дифференцируемых на
функций.
7. На множестве всех определенных и ограниченных на функций зададим следующим образом
![]() .
Полученное таким образом пространство
обозначается символом
.
Полученное таким образом пространство
обозначается символом
![]() и называется пространством ограниченных
на
функций.
и называется пространством ограниченных
на
функций.
8. Пусть
фиксированное
число
,
на множестве всех вещественных функций
![]() каждая из которых удовлетворяет 3
условиям:
каждая из которых удовлетворяет 3
условиям:
1) - определена на
2) - измерима по Лебегу на
3)
![]() -
интегрируема по Лебегу на
.
-
интегрируема по Лебегу на
.
Зададим
следующим образом:
 .
Полученное таким образом пространство
обозначается символом
.
Полученное таким образом пространство
обозначается символом
![]() и называется пространством суммируемых
со степенью
на
функций.
и называется пространством суммируемых
со степенью
на
функций.
Сходимость последовательностей элементов метрических пространств.
Будем говорить,
что последовательность элементов
![]() метрического пространства
,
является сходящейся (сх) в этом пространстве
к элементу
метрического пространства
,
является сходящейся (сх) в этом пространстве
к элементу
![]() ,
если:
,
если:
![]() .
.
Св-ва:
1)всякая сходящаяся последовательность элементов метрического пространства сходится к единственному элементу этого пространства;
2)каждая сходящаяся последовательность метрического пространства является ограниченной;
3)любая подпоследовательность сходящейся последовательности элементов метрического пространства сходится к тому же элементу этого пространства, что и сама последовательность;
4) всякая сходящаяся последовательность элементов метрического пространства сходится в себе;
5) всякая сходящаяся в себе последовательность элементов метрического пространства является ограниченной.
