
- •2) Электростатическое поле и его силовые характеристики.
- •3) Поток напряженности электрического поля
- •2) Потенциал и его связь с напряженностью электростатического поля.
- •3) Основные уравнения электростатики.
- •6) Проводники в электрическом поле.
- •7) Энергия электрического поля в конденсаторе.
- •6) Закон Джоуля-Ленца в дифференциальной и интегральной форме.
- •7) Правило Кирхгофа.
- •2) Закон Био-Савара-Лапласа.
- •2) Намагниченность.
- •3) Магнитные восприимчивость и проницаемость.
- •4) Температура Кюри. Домены.
- •5) Магнетизм горных пород. Палеомагнетизм.
- •5) Индуктивность длинного соленоида и Энергия магнитного поля.
- •6) Взаимоиндукция
- •7) Трансформация токов и напряжений.
- •8) Сейсмографы.
- •3) Мощность переменного тока.
- •2) Дифференциальное уравнение собственных электромагнитных колебаний в контуре.
- •3) Затухающие колебания.
- •2) Основные положения теории Максвелла.
- •3) Вихревое электрическое и потенциальное магнитное поле.
- •5) Уравнения Максвелла в интегральной форме.
- •6) Электромагнитные волны и их свойства.
- •7) Шкала электромагнитных волн.
- •2) Излучение и поглощение света.
- •3) Спектры. Основы спектрального анализа.
- •8) Принцип действия лазера.
- •4) Распределение интенсивности света в интерференционном поле.
- •5) Интерференция в тонких пластинах. Интерферометры.
- •2) Принцип Гюйгенса-Френеля.
- •3) Дифракция Френеля и Фраунгофера.
- •4) Дифракционная решетка.
- •5) Дифракционные спектры и спектрографы.
- •6) Дифракция рентгеновских лучей в кристаллах.
- •7) Формула Вульфа-Брэггов.
- •2) Закон Малюса. Закон Брюстера.
- •3) Двойное лучепреломление в одноосных кристаллах.
- •4) Вращение плоскости поляризации.
- •5) Методы поляризационного анализа горных пород.
- •6) Нормальная и аномальная дисперсия света.
- •4) Гипотеза де Бройля.
- •6) Квантовые числа.
- •9) Энергия связи нуклонов в ядре и дефект массы.
- •10) Взаимные превращения нуклонов.
- •13) Термоядерный синтез и проблема управляемых термоядерных реакций.
5) Уравнения Максвелла в интегральной форме.
Первое уравнение Максвелла является обобщением на переменные поля эмпирического Ампера закона о возбуждении магнитного поля электрическими токами. Максвелл высказал гипотезу, что магнитное поле порождается не только токами, текущими в проводниках, но и переменными электрическими полями в диэлектриках или вакууме. Величина, пропорциональная скорости изменения электрического поля во времени, была названа Максвеллом током смещения. Ток смещения возбуждает магнитное поле по тому же закону, что и ток проводимости (позднее это было подтверждено экспериментально). Полный ток, равный сумме тока проводимости и тока смещения, всегда является замкнутым.
Первое уравнение Максвелла имеет вид:
![]() ,
(1, a)
,
(1, a)
то
есть циркуляция вектора напряжённости
магнитного поля вдоль замкнутого контура
L
(сумма скалярных произведений вектора
Н
в данной точке контура на бесконечно
малый отрезок dl
контура) определяется полным током
через произвольную поверхность S,
ограниченную данным контуром. Здесь jn
— проекция
плотности тока проводимости j
на нормаль к бесконечно малой площадке
ds, являющейся
частью поверхности S,
![]() —
проекция плотности тока смещения на ту
же нормаль, а с
= 3×1010
см/сек —
постоянная,
равная скорости распространения
электромагнитных взаимодействий в
вакууме.
—
проекция плотности тока смещения на ту
же нормаль, а с
= 3×1010
см/сек —
постоянная,
равная скорости распространения
электромагнитных взаимодействий в
вакууме.
Второе уравнение Максвелла является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная) записывается в виде:
![]() ,
(1, б)
,
(1, б)
то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь Bn — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствует Ленца правилу для направления индукционного тока.
Третье уравнение Максвелла выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):
![]() ,
(1, в)
,
(1, в)
то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.
Четвёртое уравнение Максвелла (обычно называемое Гаусса теоремой) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:
![]() ,
(1, г)
,
(1, г)
то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном данной поверхностью).
6) Электромагнитные волны и их свойства.
|
Электромагнитные волны. Из уравнений Максвелла вытекает вывод о существовании электромагнитных волн. Для того, чтобы показать это, рассмотрим уравнения (I) и (III) в применении к конкретным полям. Пусть имеется некоторая система координат Х,Y,Z, как показано на рис.36, и в начале координат какими-то внешними причинами созданы электрическое и магнитное поля, характеризующиеся векторами Е и В соответственно. Направления этих векторов указаны на рис. |
Выберем малые прямоугольники со сторонами dx, dy и dz (см. рис.) Вычислим циркуляции
векторов Е и В по периметру прямоугольников. Для вычисления используем тот же прием, с помощью которого была определена величина вектора магнитной индукции на оси длинного соленоида. Направление обхода контуров выберем по часовой стрелке, и учтем, что величины Е и В могут зависеть от х. На расстоянии dx от начала координат они принимают значения Е + dЕ и В + dВ соответственно. При этих условиях
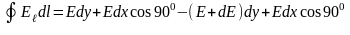 или
или
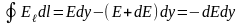 .
.
Аналогично для вектора В
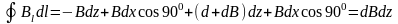 .
.
Значения (E+dE)dy и Bdz взяты со знаком минус потому, что вектора на соответствующих отрезках направлены против выбранного обхода контуров. Подставляя вычисленные значения циркуляции в уравнения (I) и (III), получим:
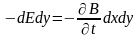 и
и
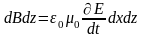 ,
откуда
,
откуда
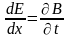 ;
;
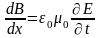 ,
где производная по х имеет смысл
частной производной, поэтому правильнее
заменить знак
,
где производная по х имеет смысл
частной производной, поэтому правильнее
заменить знак
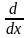 на знак частной производной
на знак частной производной
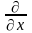 :
:
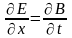 ;
;
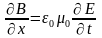 .
.
Дифференцируя
первое уравнение по х, а второе – по t,
и сравнивая полученные результаты,
имеем:
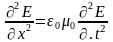 .
.
Из курса механики
известно, что это уравнение относится
к так называемым волновым уравнениям,
решению которых соответствует бегущая
волна. Скорость распространения волны
определяется коэффициентом, стоящим
перед второй производной по времени:
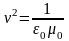 .
.
Аналогичное уравнение может быть получено и для вектора магнитной индукции В.Из уравнений (I) и (III) следует, что электрический и магнитный вектора связаны между собой,
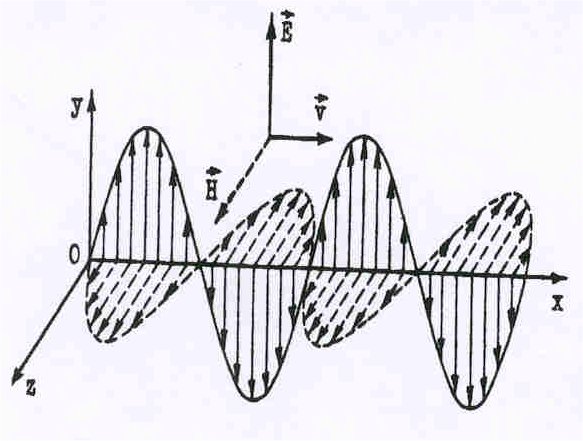
Рис.37. Структура электромагнитной волны. |
поэтому волны названы электромагнитными. Подставляя численные значения 0 и 0 ,получим, что v = c = 3108 м/c, т.е. скорость распространения электромагнитной волны равна скорости света. Если волна распространяется в среде, характеризующейся постоянными и , то скорость электромагнитной волны
Электромагнитные волны обладают следующими свойствами: |
волны поперечны, т.к. вектора Е и В направлены по осям Y и Z, тогда как волна распространяется вдоль оси Х.
волны поляризованы, т.к. изменяющееся магнитное поле перпендикулярно индуцированному им электрическому.
Это электрическое поле создает переменное магнитное, плоскость колебаний которого совпадает с плоскостью первичного магнитного поля (см. рис.37) так, что магнитное поле сохраняет свою ориентацию в пространстве. Если в любой плоскости, перпендикулярной направлению распространения, значения Е и В не зависят от координат, то волна называется плоской, и ее можно записать так:
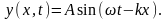
В этом выражении
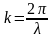 -
волновое число,
= сТ, =2/T.
Формула плоской электромагнитной волны
будет часто использоваться при
рассмотрении оптических явлений.
Световыми являются волны, длина которых
лежит в интервале от 0,4 до 0,7 мкм. Волна,
в которой колебания имеют одну частоту,
называется монохроматической
(одноцветной). Белый свет содержит не
менее семи основных цветов. Для упрощения
математических выкладок часто
ограничиваются рассмотрением
монохроматических волн.
-
волновое число,
= сТ, =2/T.
Формула плоской электромагнитной волны
будет часто использоваться при
рассмотрении оптических явлений.
Световыми являются волны, длина которых
лежит в интервале от 0,4 до 0,7 мкм. Волна,
в которой колебания имеют одну частоту,
называется монохроматической
(одноцветной). Белый свет содержит не
менее семи основных цветов. Для упрощения
математических выкладок часто
ограничиваются рассмотрением
монохроматических волн.

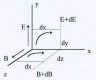 Рис.36. К вычислению циркуляций для
векторов Е и В.
Рис.36. К вычислению циркуляций для
векторов Е и В.
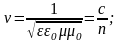
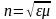 - показатель преломления среды
относительно вакуума.
- показатель преломления среды
относительно вакуума.