3) Мощность переменного тока.

При протекании переменного тока по участку цепи электромагнитное поле совершает работу, и в цепи выделяется джоулево тепло. Мгновенная мощность в цепи переменного тока равна произведению мгновенных значений тока и напряжения: p = J · u. Практический интерес представляет среднее за период переменного тока значение мощности

Здесь I₀ и U₀ – амплитудные значения тока и напряжения на данном участке цепи, φ – фазовый сдвиг между током и напряжением. Черта означает знак усреднения. Если участок цепи содержит только резистор с сопротивлением R, то фазовый сдвиг φ = 0:

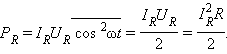
Для того, чтобы это выражение по виду совпадало с формулой для мощности постоянного тока, вводятся понятия действующих или эффективных значений силы тока и напряжения:

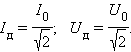
Средняя мощность переменного тока на участке цепи, содержащем резистор, равна

Если участок цепи содержит только конденсатор емкости C, то фазовый сдвиг между током и напряжением Поэтому

Аналогично можно показать, что P_L = 0.

Таким образом, мощность в цепи переменного тока выделяется только на активном сопротивлении. Средняя мощность переменного тока на конденсаторе и катушке индуктивности равна нулю.

Рассмотрим теперь электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки. Цепь подключена к источнику переменного тока частоты ω. На всех последовательно соединенных участках цепи протекает один и тот же ток. Между напряжением внешнего источника e (t) и током J (t) возникает фазовый сдвиг на некоторый угол φ. Поэтому можно записать

J (t) = I0 cos ωt;   e (t) =  0 cos (ωt + φ).

Средняя мощность, развиваемая источником переменного тока, равна

U_R =  ₀ · cos φ, поэтому Следовательно, вся мощность, развиваемая источником, выделяется в виде джоулева тепла на резисторе.

9.Электромагнитные колебания. Дифференциальное уравнение собственных электромагнитных колебаний в контуре. Затухающие колебания. Добротность контура. Вынужденные колебания. Резонанс напряжений и токов.

1) Электромагнитные колебания.

Периодические изменения во времени электрического заряда (силы тока, напряжения) называются электромагнитными колебаниями.

Электрическая цепь, состоящая из последовательно соединенных конденсатора с емкостью C  и катушки с индуктивностью L, называется колебательным контуром.

Электромагнитными колебаниями являются радиоволны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи, гамма-лучи.

Электромагнитные колебания представляют собой совокупность фотонов, и только при большом числе фотонов их можно рассматривать как непрерывный процесс.

Различают вынужденные электромагнитные колебания, поддерживаемые внешними источниками, и собственные электромагнитные колебания, существующие и без них.

2) Дифференциальное уравнение собственных электромагнитных колебаний в контуре.

В момент времени t=0 заряд на пластинах конденсатора Q₀, разность потенциалов максимальна U_0,, ток в цепи равен нулю. После отключения внешнего источника напряжения и замыкания цепи появляется ток разрядки, вызывающий возникновение ЭДС самоиндукции: ЭДС_инд = .

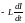В любой замкнутой цепи сумма падений напряжения на всех элементах цепи равна сумме действующих в этой цепи ЭДС. При R=0 падение напряжения есть только на пластинах конденсатора U = 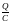. Внешний источник напряжения отключен, поэтому единственной ЭДС в рассматриваемой цепи будет ЭДС индукции. Таким образом U = ЭДС_ин , отсюда. 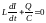. Учитывая, что 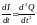, получаем дифференциальное уравнение вида 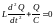или . 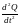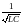Введем стандартные обозначения: Q’’ = и _o = , получаем дифференциальное уравнение электромагнитных колебаний в контуре без активного сопротивления в стандартной форме: Q’’ + _oQ = 0.