5. Волновые свойства частиц
5.1. Теоретическое введение.
Уравнение Шредингера описывает изменение во времени состояния квантовых объектов, характеризуемых волновой функцией.
Вид волновой функции или пси-функции получается из решения уравнения Шредингера, которое выглядит следующим образом
(5.1)
Здесь m– масса частицы,i–мнимая единица,– оператор Лапласа, результат действия которого на некоторую функцию представляет собой сумму вторых производных по координатам
.
Буквой Uв уравнении (5.1) обозначена функция координат и времени, градиент которой, взятый с обратным знаком, определяет силу, действующую на частицу.
В случае, когда функция Uне зависит от времени, она имеет смысл потенциальной энергии частицы. В этом случае решение уравнения Шредингера распадается на два множителя, один из которых зависит только от координат, другой – только от времени:
. (5.2)
Уравнением Шредингера для стационарного состояния.
. (5.3)
Физический смысл пси-функции: квадрат модуля пси-функции (волновой функции) определяет вероятность dPтого, что частица будет обнаружена в пределах объемаdV.
. (5.4)
(А– коэффициент пропорциональности).
Интеграл от выражения (5.5), взятый по всему объему, должен равняться единице
. (5.5)
В квантовой механике принимается, что
волновая функция допускает умножение
на отличное от нуля произвольное
комплексное число С, причем
и
описывают
одно и то же состояние частицы. Это
позволяет выбрать волновую функцию
так, чтобы она удовлетворяла условию
(5.6)
Условие (5.6) носит название условия нормировки. Функции, удовлетворяющие этому условию, называются нормированными.
В соответствии со своим смыслом пси-функция должна быть однозначной, непрерывной и конечной (за исключением, быть может, особых точек). Кроме того, она должна иметь непрерывную и конечную производную. Совокупность перечисленных требований носит название стандартных условий.
Вероятность Робнаружить частицу в интервале отх1дох2находится интегрированием
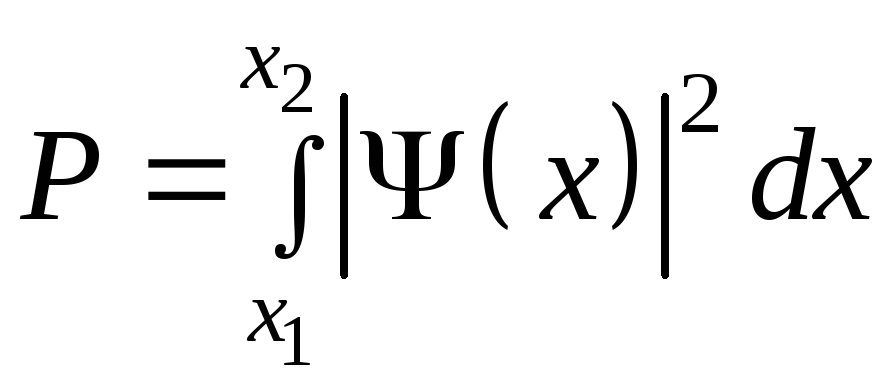. (5.7)
Собственные значения энергии частицы в бесконечно глубокой потенциальной яме принимают только дискретные значения
(n = 1, 2, 3, ...). (5.8)
Соответствующие этой энергии собственные волновые функции имеют вид
(n = 1, 2, 3, ...). (5.9)
Коэффициент прозрачности Dпрямоугольного потенциального барьера конечной ширины
, (5.10)
где U0– высота потенциального барьера,Е– энергия частицы,
– ширина барьера.
Коэффициент отражения R и коэффициент прозрачностиDсвязаны соотношением
. (5.11)
Коэффициент отражения Rи коэффициент прохожденияDдля низкого (E > U0) потенциального барьера бесконечной ширины
;
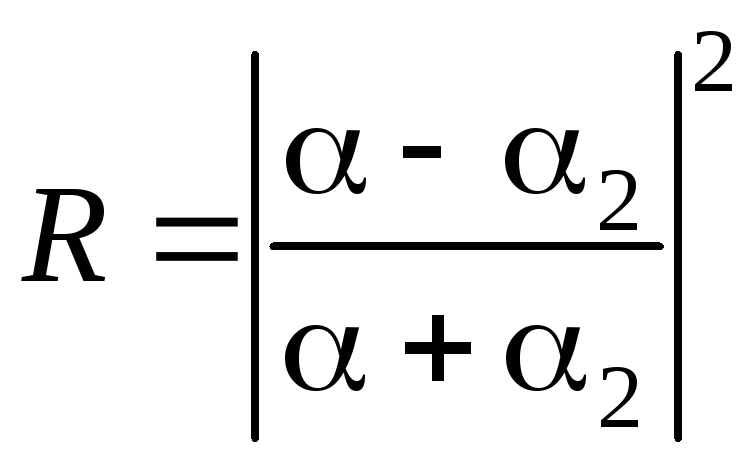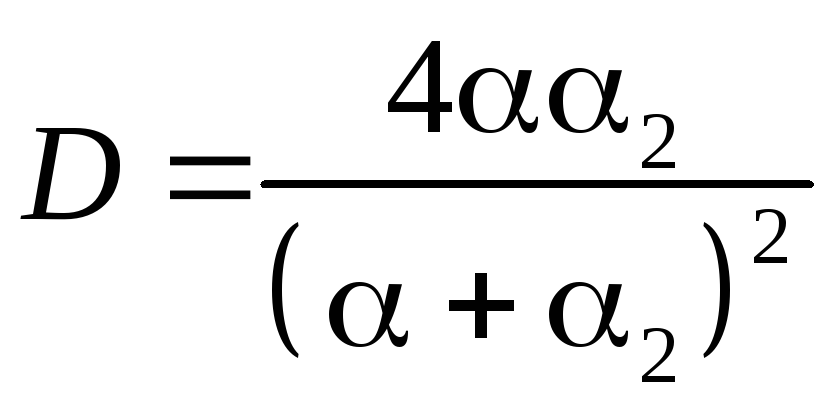, (5.12)
где
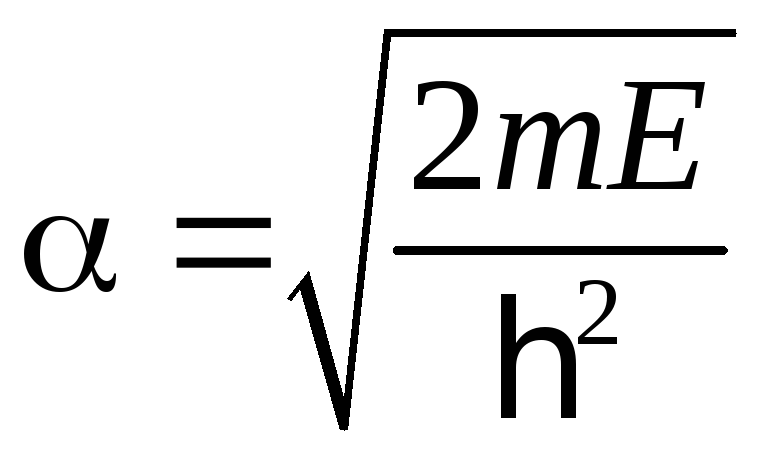и
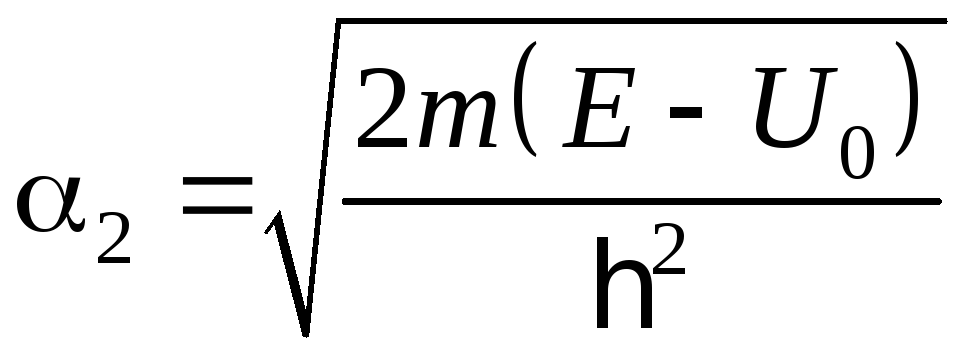– волновые числа волн де Бройля.
5.2. Теоретическое задание
Покажите, что уравнение Шредингера в случае независимости от времени потенциальной энергии переходит в стационарное уравнение Шредингера.
5.3. Индивидуальное задание
Частица находится на N-м уровне в одномерной потенциальной яме с бесконечно высокими стенками. Ширина ямы равна 10 нм. Определить вероятность нахождения частицы в первой трети ямы.
При какой ширине потенциальной ямы дискретность энергии электрона, находящегося на N-м энергетическом уровне становится сравнимой с энергией теплового движения при температуреТ= 300 К?
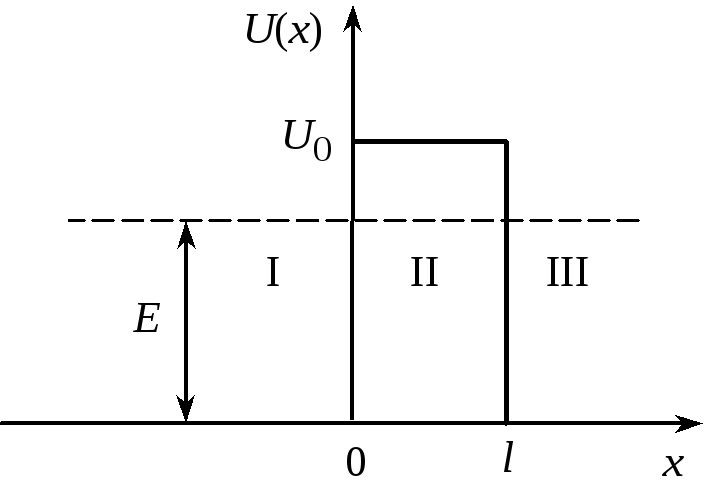
Частица движется в положительном направлении оси х. Энергия частицыЕ=LэВ, высота полубесконечного барьераU= (M + 1)/2 эВ. Определите коэффициент отражения на границе.
Частица движется в положительном направлении оси х. Энергия частицыЕ= 2МэВ, высота прямоугольного потенциального барьераU0= (2M +L) эВ, ширина потенциального барьера
= 0,01Nнм. Определите
коэффициенты прозрачностиDи отраженияRбарьера.
Изобразите на рисунке примерный вид
волновой функции (ее действительной
части) в пределах каждой из областейI,II,III,
при условии пренебрежения отраженными
волнами на границахI–IIиII–III(см. рис.)
