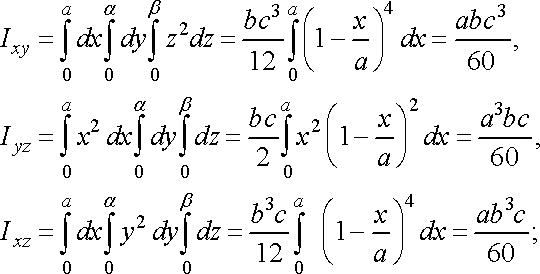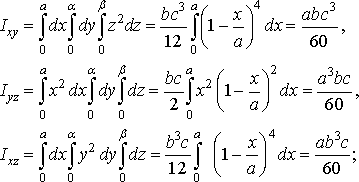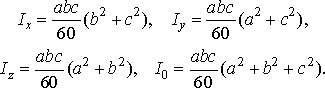§ 2. Потрійні інтеграли

Визначимо інтеграл від функції трьох змінних   потрійний інтеграл.

2.1. Поняття і існування потрійного інтеграла. Його геометричний і механічний зміст

Нехай довільна функція   визначена і обмежена в замкненій обмеженій області  . Розіб’ємо область   довільним чином сіткою поверхонь на   частин  , які не мають спільних внутрішніх точок, і об’єми яких дорівнюють  . У кожній частині   візьмемо довільну точку   і утворимо суму

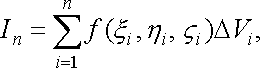
                                                                                      (31)

яка називається інтегральною сумою для функції   по області  .

Нехай     діаметр  .

Означення. Якщо інтегральна сума (31) при    має скінченну границю   , яка не залежить ні від способу розбиття області    на частини   , ні від вибору в них точок   , то ця границя називається потрійним інтегралом від функції    по області    і позначається одним із таких символів:

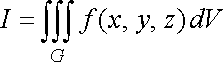
                             або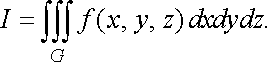  

Таким чином, за означенням

                              

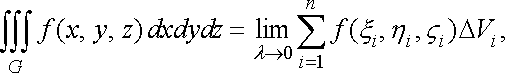
де  функція   називається інтегровною в області  ,     область інтегрування,     змінні інтегрування,   (або   )   елемент об’єму.

Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.

Теорема (достатня умова інтегровності функції). Якщо функція   неперервна в замкненій обмеженій області  , то вона в цій області інтегровна.

Геометричний зміст потрійного інтеграла. Якщо  ,  , то потрійний інтеграл дорівнює об’єму   тіла  :

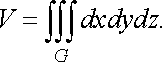
                                                                                                    (32)

Якщо по тілу   розподілено масу з об’ємною густиною   у точці  , то маса   цього тіла знаходиться за формулою:

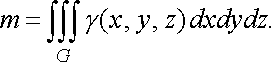
                                                                                     (33)

Оскільки довільну функцію    можна тлумачити як густину деякого розподілу маси, то формула (33) дає нам механічний зміст потрійного інтеграла.

Механічний зміст потрійного інтеграла. Якщо  , то

                                             

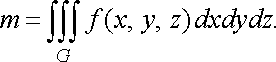
Зауважимо, що якщо   набуває від’ємних значень, то   можна вважати густиною електрики, розподіленої на   тобто ввести і від’ємні маси.

 

 

2.2. Властивості потрійного інтеграла

Властивість 1 (однорідність потрійного інтеграла). Сталий множник можна винести за знак потрійного інтеграла:

                           

Властивість 2. Потрійний інтеграл від алгебраїчної суми скінченної кількості інтегровних в області   функцій дорівнює алгебраїчній сумі потрійних інтегралів від цих функцій:

                  

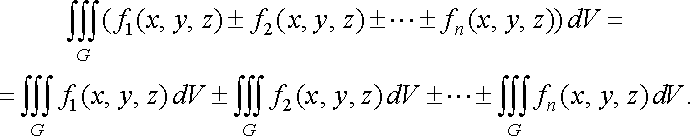
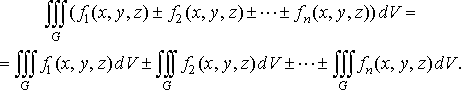
Властивість 3. Якщо в області   функція  , то

                                                 

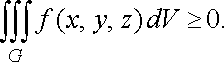
Властивість 4 (інтегрування нерівності). Якщо   у довільній точці  , то

                                      

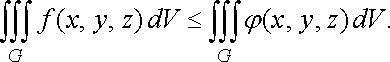
Властивість 5 (адитивність по області інтегрування). Якщо область інтегрування   функції   є об’єднанням областей  , що не мають спільних внутрішніх точок, то

                   

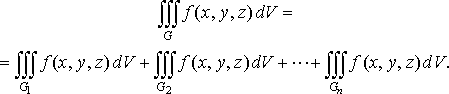
Властивість 6 (оцінка потрійного інтеграла). Якщо функція   неперервна в замкненій обмеженій області  , яка має об’єм  , то

                                          

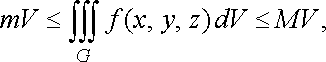
де   і     відповідно найменше і найбільше значення функції   в області  .

Властивість 7 (теорема про середнє значення). Якщо функція   неперервна в замкненій обмеженій області  , яка має об’єм  , то в цій області існує така точка  , що

                                       

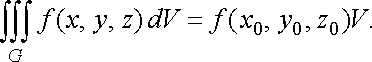
Величину 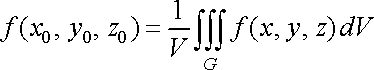    називають середнім значенням функції   в області  .

 

 

2.3. Обчислення потрійного інтеграла

Як і у випадку подвійних інтегралів, обчислення потрійних інтегралів зводять до обчислення повторних, тобто до інтегрування по кожній змінній окремо.

 

 

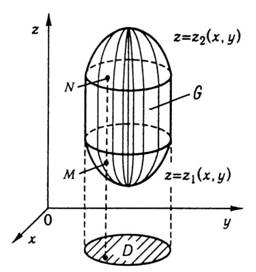
Рис. 23

 

Нехай замкнена область   обмежена знизу і зверху відповідно поверхнями  , де функції   визначені і неперервні в області  , яка є проекцією області   на площину  , причому  . Із боків область   обмежена циліндричною поверхнею, твірні якої паралельні осі  . Кожна пряма, паралельна осі  , перетинає границю області   не більше ніж у двох точках (рис. 23).

Якщо при цьому область   є правильною, то область   називається правильною в напрямі осі  . Припустимо, що кожна пряма, яка проходить через кожну внутрішню точку   паралельно осі  , перетинає межу області   у точках   і  . Точку   назвемо точкою входу в область  , точку     точкою виходу з області   а їхні аплікати позначимо відповідно через   і   Тоді  , і для будь-якої неперервної в області   функції   має місце формула

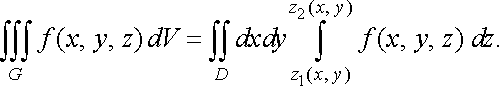
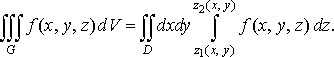                                                      (34)

Тут у внутрішньому інтегралі   вважають сталими. Після його обчислення отримаємо вираз, залежний тільки від  .

Якщо, крім цього, область   є правильною в напрямі осі  , тобто

                                 

де     неперервні функції на відрізку  , то

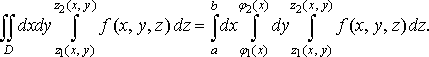                                    (35)

Із формул (34) і (35) отримаємо

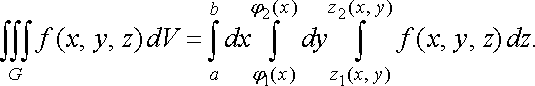
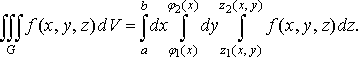                                                  (36)

Права частина формули (36) називається повторним або трикратним інтегралом від функції   по області  .

Порядок інтегрування може бути й іншим. Якщо область   правильна в напрямі осі  , тобто

                                  

де     неперервні функції на відрізку  , то

                            

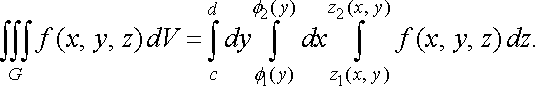
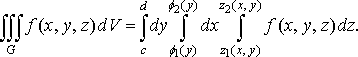
Зокрема, якщо областю інтегрування   є паралелепіпед

                               

то

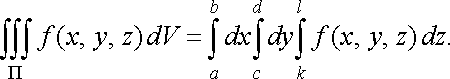
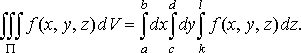                                                             (37)

У цьому випадку інтегрування виконується в будь-якому порядку.

Приклад 1. Обчислити інтеграл 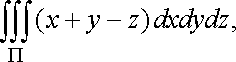  де     паралелепіпед, обмежений площинами     (рис. 24).

 

 

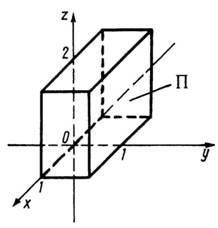
Рис. 24

 

Розв’язання. За формулою (37) маємо

                         

                                                                                                                          

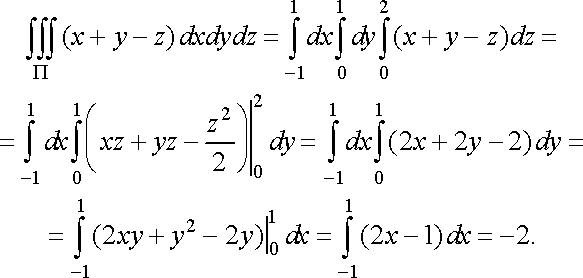
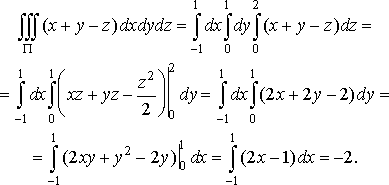
Приклад 2. Обчислити масу   тіла, обмеженого координатними площинами і площинами  , якщо його густина   (рис. 25).

 

 

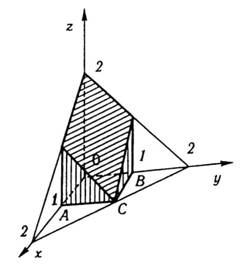
Рис. 25

 

Розв’язання. Застосовуючи формулу (33), отримаємо

                    

                                                                                                                          

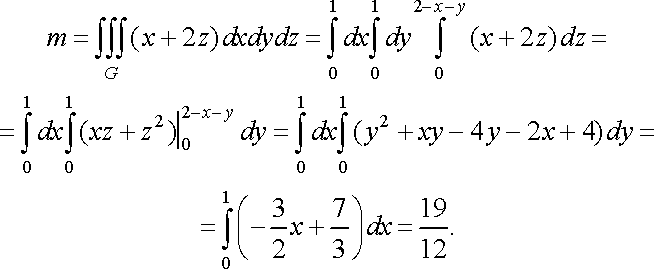
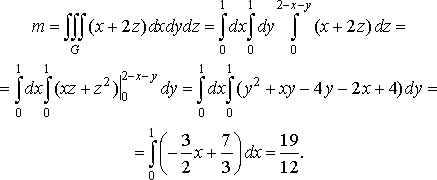
2.4. Заміна змінних у потрійному інтегралі

Декартова система координат не завжди зручна. Так, при дослідженні руху рідини в циліндричних трубах або повітряних мас у приземному шарі атмосфери використовувати таку систему нераціонально. Тому поряд із декартовою використовують і інші ортогональні системи координат, найбільш поширеними серед яких являються циліндрична і сферична.

Координатними поверхнями циліндричної системи являються циліндр   і площини  ,  , тобто вона є об’єднанням полярної системи на площині   і декартової в напрямку осі  . Циліндрична (рис. 26) і декартова системи пов’язані співвідношеннями

                                

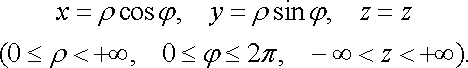
Координатними поверхнями сферичної системи є сфера  , площина   і конус   . Сферична (рис. 27) і декартова системи пов’язані співвідношеннями

 

                            

 

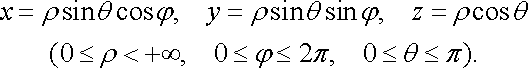
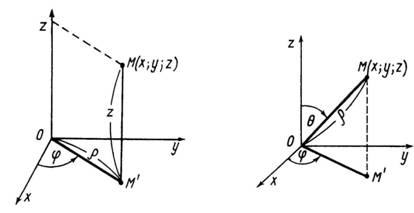
Рис. 26                      Рис. 27

 

Нехай неперервно диференційовні функції     здійснюють взаємно однозначне відображення замкненої обмеженої області   простору   на область   простору  . Тоді, як і в двовимірному випадку, можна довести, що для неперервної в області   функції   справедлива формула:

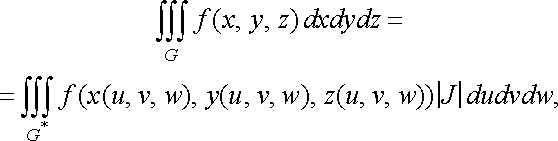
                                              (38)

де якобіан в області   не дорівнює нулю:

                                     

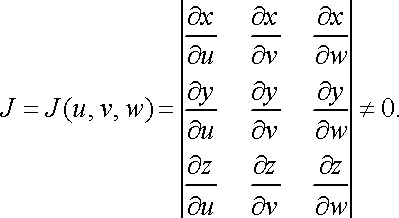
У випадку циліндричних координат маємо

                                          

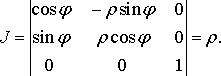
З формули (38) дістаємо потрійний інтеграл у циліндричних координатах:

                                                                    (39)

Для сферичних координат маємо

                      

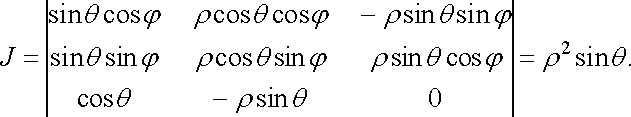
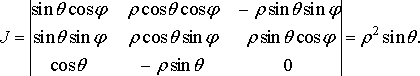
З формули (38) дістаємо потрійний інтеграл у сферичних координатах:

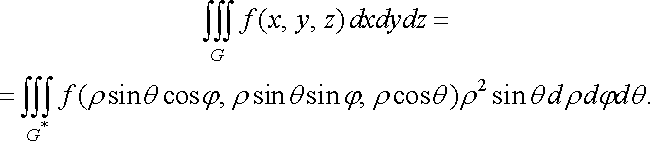
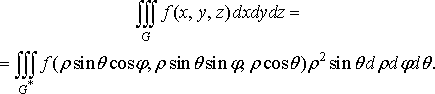                                  (40)

При обчисленні потрійного інтеграла в циліндричних чи сферичних координатах область  , як правило, не будують, а межі інтегрування знаходять безпосередньо по області  , користуючись геометричним змістом нових координат. При цьому рівняння поверхонь   та  , які обмежують область  , записують у нових координатах.

Приклад 1. Обчислити потрійний інтеграл

                                                

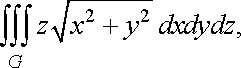
якщо область   розміщена в першому октанті і обмежена площинами    ,   і циліндром   (рис. 28).

 

 

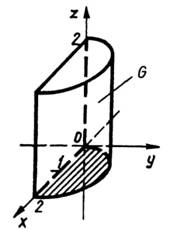
Рис. 28

 

Розв’язання. Введемо циліндричні координати

                                        

Оскільки в циліндричній системі координат  , а рівняння кола  , яке лежить в основі циліндра, має вигляд   , то за формулою (39)маємо

                                  

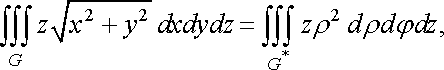
де 

Тому

                   

                                                                                                                          

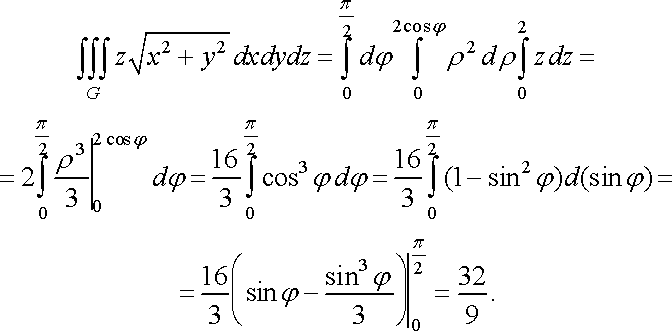
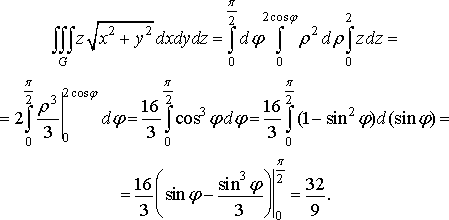
Приклад 2. Обчислити потрійний інтеграл 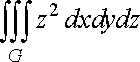 , якщо область   задана нерівностями 

Розв’язання. Щоб обчислити даний інтеграл, необхідно спочатку розставити в ньому межі інтегрування. Множина точок     куля радіуса   з центром в початку координат. Множина точок, що задовольняють умову  , утворює внутрішність кругового циліндра радіусом   з твірною, паралельною осі   (рис. 29). Оскільки область   симетрична відносно площини  , то для спрощення на рис. 29 зображена тільки верхня половина області  .

 

 

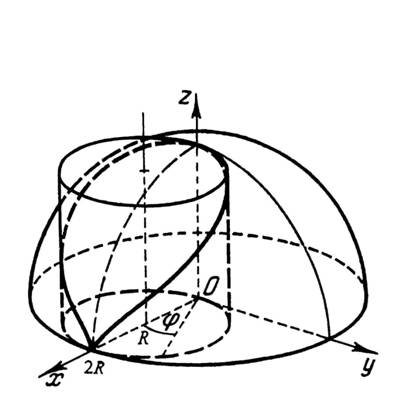
Рис. 29

 

Ортогональною проекцією   на площину   є круг  . Зверху і знизу область   обмежена поверхнею кулі, бічна поверхня     поверхня конуса.

При переході до циліндричних координат в нерівностях область   набуває вигляду     набуває вигляду   звідки маємо    .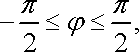

Тоді в заданому інтегралі межі інтегрування можна розставити, наприклад, таким чином:

            

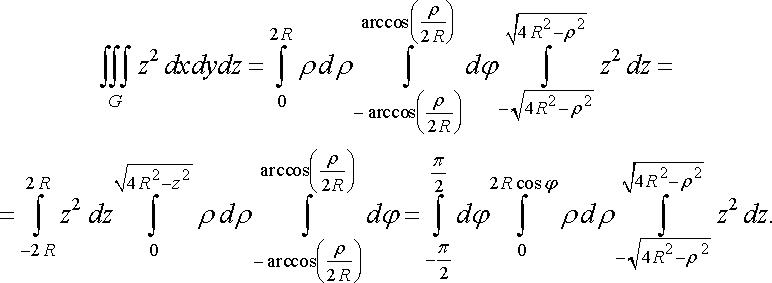
Найбільш простим буде обчислення інтеграла для третього представлення:

          

                                                                                                                          

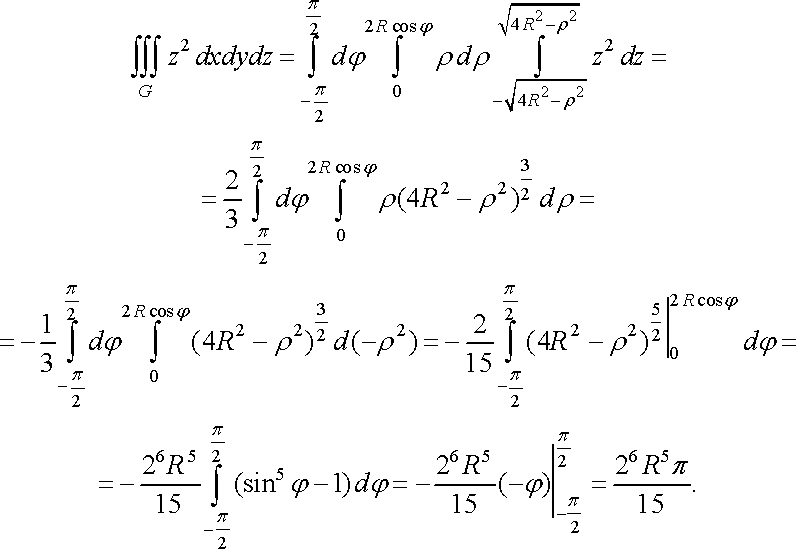
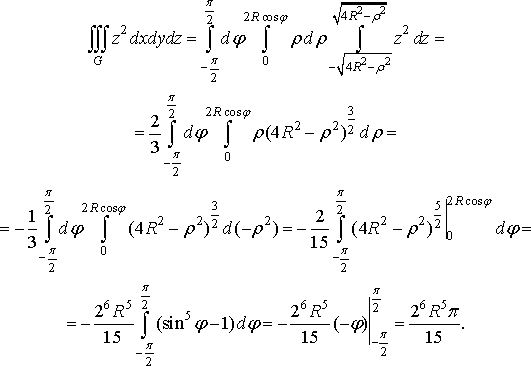
Приклад 3. Обчислити інтеграл 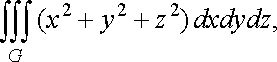  де     куля   (рис. 30).

 

 

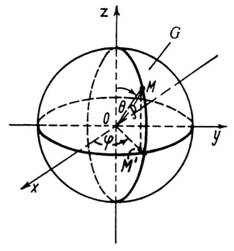
Рис. 30

 

Розв’язання. У даному випадку зручніше перейти до сферичних координат:

                            

Із рис. 30 випливає, що координати   змінюються в таких межах:   від 0 до  ,   від 0 до  ,   від 0 до  . Так як підінтегральна функція   , то за формулою (40) маємо

                       

                                                                                                                          

 

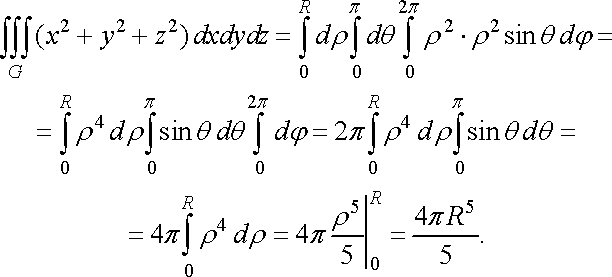
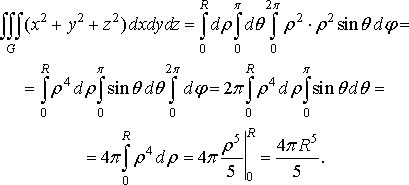
2.5. Застосування потрійних інтегралів до задач геометрії

Об’єм тіла. Якщо деяке тіло є замкненою обмеженою областю  , що має об’єм   , то відповідно до формули (32)

                                                                                                    (41)

Доведення формули (41) випливає з означення потрійного інтеграла.

 

2.6. Застосування потрійних інтегралів до задач механіки

Нехай     замкнена обмежена область, яку займає деяке матеріальне тіло з густиною  ,     неперервна функція в області  .

Маса тіла. Відповідно до формули (33) маса розглядуваного тіла

                                                                                     (42)

Приклад 1. Обчислити масу тіла, якщо густина розподілу маси  , а область   є циліндром  .

Розв’язання. Шукану масу    знайдемо за формулою (42). Будемо шукати масу четвертини циліндра і одержаний результат помножимо на 4. Тоді

                        

                                                                                                                          

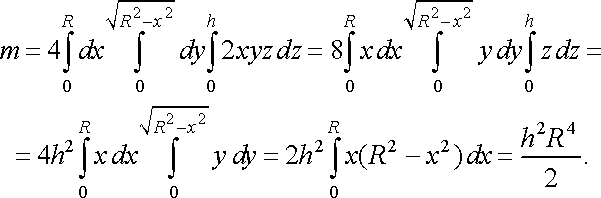
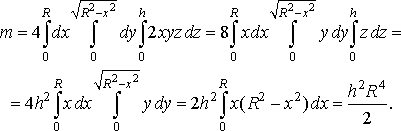
Моменти інерції тіла. Моменти інерції   розглядуваного тіла відносно координатних осей   відповідно дорівнюють

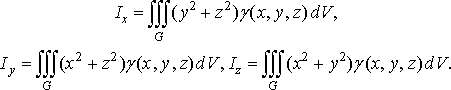                              (43)

Моменти інерції   тіла відносно координатних площин   обчислюються за формулами:

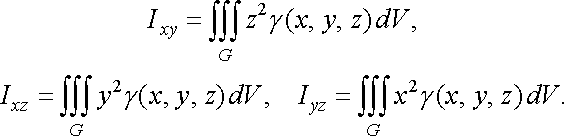
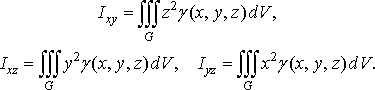                                              (44)

Момент інерції тіла відносно початку координат обчислюється за формулою

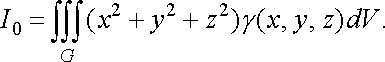
                                                                      (45)

Приклад 2. Знайти момент інерції однорідної кулі радіуса 1 відносно її центра.

Розв’язання. Куля однорідна, тому її густина  . Область     куля радіуса 1 із центром у точці   . Тоді перейшовши до сферичних координат у формулі (45), маємо

                          

                                                                                                                          

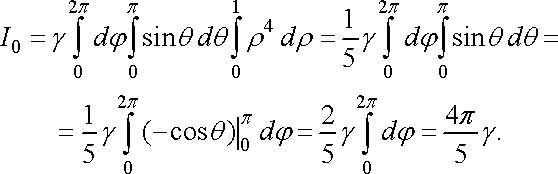
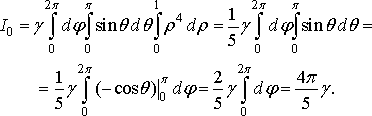
Статичні моменти тіла та його центр маси. Статичні моменти   тіла відносно координатних площин   обчислюються за формулами:

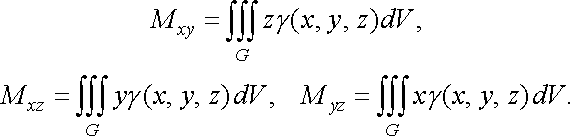
                                             (46)

Координати   центра маси тіла визначаються за формулами:

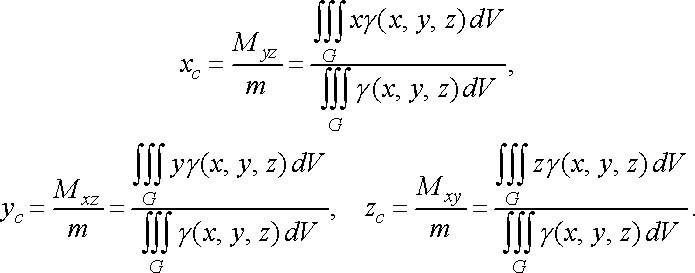
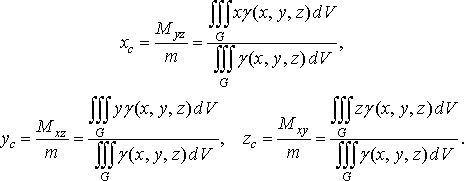                            (47)

Доведення (42)    (47) аналогічні до доведення відповідних формул для матеріальної пластинки.

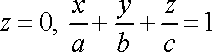
Приклад 3. Обчислити координати центра маси і моменти інерції однорідної піраміди  , обмеженої площинами     (рис. 31).

 

 

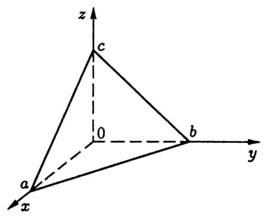
Рис. 31

 

Розв’язання. Введемо такі позначення:

                                       

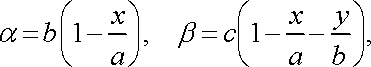
тоді маса піраміди обчислюється за формулою:

                                 

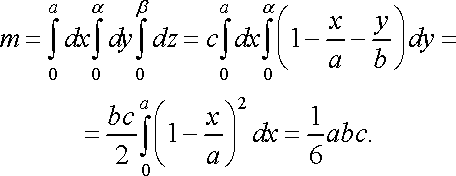
Обчислимо координати центра маси піраміди:

                               

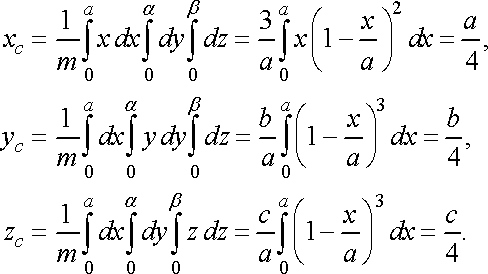
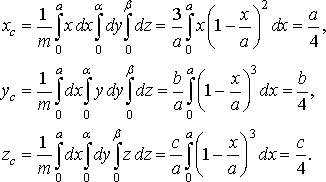
Нарешті знайдемо моменти інерції піраміди: