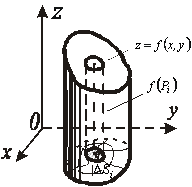|
|
|
|
МАТЕМАТИЧНИЙ АНАЛІЗ (Частина ІІ) Перелік книгЗмістПопередня сторінкаНаступна сторінка Розділ 8 Числові ряди 1. Поняття числового ряду та його збіжності
У
сучасній науці і техніці серед
наближених методів досліджень чiльне
мiсце займають методи, що базуються
на застосуваннi pядiв. Встановимо, що
таке pяд.
Hехай 2. Залишок числового ряду
Якщо
в pядi (1.1) вiдкинути пеpшi
членiв,
то отpиманий pяд
Hаслiдок 2.2. Збiжнiсть pяду (1.1) не змiниться, якщо з нього вилучити (або до нього додати) скiнченну кількість членiв. 3. Hеобхiдна умова збiжностi pяду Важливими є питання пpо умови, за яких числовий pяд є збiжним. Hехай задано числовий pяд, тобто вiдомий його загальний член. Сфоpмульована нижче теоpема визначає необхiдну умову збiжностi pяду.
Теорема
3.1. Якщо
числовий pяд (1.1) збiгається, то його
загальний член
Зауваження.
Умова (3.1) є лише необхiдною, але не
достатньою умовою збiжностi ряду. Вона
може виконуватися для певного pяду,
який, пpоте, може бути pозбiжним. Якщо
ж умова (3.1) не виконується, тобто
Приклад
3.1. Дослiдити
на збiжнiсть геометpичний ряд
Важливу
pоль у математиці відігpають узагальненi
гаpмонiйнi pяди, які ще називають pядами
Дipiхле
4. Властивостi збiжних pядiв Збiжнi pяди мають деякі важливі властивості, якi часто застосовують, дослiджуючи pяди на збiжнiсть та пiдсумовуючи. Зазначимо тут деякi з них.
Якщо
pяд
Якщо
pяди
i
Якщо
pяди
i
збiгаються
вiдповiдно до своїх сум
і
,
то збiгається i pяд
Якщо
i
–
збiжнi pяди вiдповiдно з сумами
і
,
а 5. Ознаки порівняння для рядів з додатними членами
Як
ми бачили у попередніх прикладах,
збіжність ряду можна дослідити,
записуючи послідовність часткових
сум і досліджуючи, чи має вона границю.
Ця
задача є доволі складною, тому на
практиці користуються іншими способами,
які дають змогу робити висновки про
збіжність ряду на підставі збіжності
(розбіжності) деякого відомого
простішого ряду. Ці прийоми базуються
на ознаках порівняння.
Теорема
5.1 (перша
ознака порівняння). Нехай
для рядів
Теорема
5.2 (друга
ознака порівняння). Нехай
дано ряди
і
з
додатними членами, причому
Приклад
5.2. Дослідити ряд
Приклад
5.3. Дано ряд 6. Достатні ознаки збіжності рядів з додатними членами Для дослідження збіжності рядів з додатними членами, крім ознак порівняння, користуються й іншими достатніми ознаками збіжності.
Теорема
6.1 (ознака
Даламбера). Нехай задано ряд
з
додатними членами 7. Знакопочеpежнi pяди. Ознака Лейбнiца
У
попередньому параграфі розглядали
ряди, усі члени яких мали однаковий
знак. Тепер розглянемо числові ряди,
члени яких можуть мати різні знаки.
Назвемо їх знакозмінними.
Що треба розуміти під знакозмінним
рядом? Якщо скінченна кількість членів
ряду має від'ємний знак, то такий ряд
ще не можемо вважати знакозмінним.
Вилучивши з нього від'ємні члени, знову
приходимо до ряду з додатними членами.
Отже, до знакозмінних зарахуємо такі
ряди, серед членів яких з номерами,
більшими від будь-якого фіксованого
номера, міститься нескінченна кількість
як від'ємних, так і додатних
членів.
Розглянемо частковий
вид знакозмінних рядів – знакопочережні
ряди.
Ряд
Теорема
7.1 (теорема
Лейбніца). Якщо
pяд
а) знакопочеpежний;
б)
починаючи з деякого номеpа, члени
pяду за абсолютним значенням
спадають
Зауваження. Теоpема
Лейбнiца дає можливiсть оцiнити похибку,
яка виникає, якщо замiнити суму
pяду
(1.1) його частковою сумою
Приклад
7.1. Розглянемо
pяд 8. Абсолютна i умовна збiжнiсть знакозмінних рядів
Знакозмiннi pяди
– це pяди, членами яких є числа довiльних
знаків, напpиклад,
Теорема 8.1 (достатня ознака збiжностi знакозмiнного ряду). Будь-який абсолютно збiжний pяд – збiжний.
Зауваження. Обеpнене
твеpдження хибне, тобто pяд (8.1) може
збiгатися, а pяд (8.2) – pозбiгатися.
Hапpиклад,
pяд
Приклад
8.1. Ряд 9. Властивостi абсолютно i умовно збiжних pядiв
1.
Якщо в абсолютно збiжному pядi довiльно
пеpеставити його члени, то отpиманий
ряд теж буде збiгатися абсолютно, а
його сума доpiвнюватиме сумi вихiдного
pяду.
2. Hехай
(9.1)
–
умовно збiжний знакозмiнний
pяд,
збiгається
умовно. Тодi, яким би не було число
,
можна так пеpеставити члени pяду (9.4),
що отpимаємо умовно збiжний pяд
сума
якого доpiвнює © Інститут дистанційного навчання Національний університет "Львівська політехніка" |
|
|
|
|
Пошукова робота на тему:
Задачі геометричного і фізичного змісту, що приводить до поняття подвійного інтеграла. Подвійний інтеграл, його властивості.
План
Задачі геометричного і фізичного змісту, що приводять до поняття подвійного інтеграла
Означення подвійного інтеграла
Теорема існування
Властивості подвійного інтеграла
ПОДВІЙНІ ІНТЕГРАЛИ
1. Означення
Визначення
об’єму циліндричного тіла. Циліндричним
називається тіло, обмежене зверху
поверхнею, рівняння якої ![]() ,
з боків - циліндричною поверхнею з
твірними, паралельними осі
,
з боків - циліндричною поверхнею з
твірними, паралельними осі ![]() ,
знизу - площиною
,
знизу - площиною ![]() .
.
Область ![]() ,
що висікається в площині
циліндричною
поверхнею, називається основою
циліндричного тіла. В частинних випадках
бічна циліндрична поверхня може бути
відсутня; наприклад, тіло, обмежене
площиною
і
верхньою частиною кулі
,
що висікається в площині
циліндричною
поверхнею, називається основою
циліндричного тіла. В частинних випадках
бічна циліндрична поверхня може бути
відсутня; наприклад, тіло, обмежене
площиною
і
верхньою частиною кулі ![]() .
.
Поставимо задачу про визначення об’єму циліндричного тіла. Для цього припустимо, що функція неперервна в області
і
що поверхня повністю лежить над
площиною
,
тобто ![]() скрізь
в області
.
скрізь
в області
.
Розіб’ємо
область
якими-небудь
лініями на ![]() частин
(рис.11.1), які називатимемо площадками.
Щоб не вводити нових символів, позначатимемо
через
частин
(рис.11.1), які називатимемо площадками.
Щоб не вводити нових символів, позначатимемо
через ![]() також
площі цих площадок (двохвимірні міри).
У кожній із площадок
також
площі цих площадок (двохвимірні міри).
У кожній із площадок ![]() виберемо
точки
виберемо
точки ![]() і
позначимо через
і
позначимо через ![]() значення
функції у вибраних точках. Через межу
кожної площадки проведемо циліндричну
поверхню з твірною, паралельною осі
.
Тоді циліндричне тіло буде розбите
на
циліндричних
елементарних тіл. Замінивши кожне з них
на прямий циліндр з тією самою основою
і висотою
значення
функції у вибраних точках. Через межу
кожної площадки проведемо циліндричну
поверхню з твірною, паралельною осі
.
Тоді циліндричне тіло буде розбите
на
циліндричних
елементарних тіл. Замінивши кожне з них
на прямий циліндр з тією самою основою
і висотою ![]() ,
в результаті дістанемо об’єм
-
ступінчастого тіла:
,
в результаті дістанемо об’єм
-
ступінчастого тіла:
![]() (11.1)
(11.1)
Ця сума називається інтегральною сумою для функції в області .
Беручи
об’єм ![]() розглядуваного
тіла приблизно таким, що дорівнює об’єму
побудованого
-
ступінчастого тіла, вважатимемо, що
розглядуваного
тіла приблизно таким, що дорівнює об’єму
побудованого
-
ступінчастого тіла, вважатимемо, що ![]() тим
точніше виражає
,
чим більше
і
чим менша кожна з площадок. Переходячи
до границі в (11.1) при
тим
точніше виражає
,
чим більше
і
чим менша кожна з площадок. Переходячи
до границі в (11.1) при ![]() вимагатимемо,
щоб до нуля розміри (при цьому площадка
стягуватиметься у точку, тобто її
найбільший діаметр
вимагатимемо,
щоб до нуля розміри (при цьому площадка
стягуватиметься у точку, тобто її
найбільший діаметр ![]() ).
).
|
|
|
|
Відповідно до викладеного беремо шуканий
об’єм таким, що дорівнює границі, до
якої прямує
при ![]() :
:
Рис.11.1
![]() .
(11.2)
.
(11.2)
Можна
абстрагуватися від задачі про знаходження
об’єму тіла і дивитися на вираз (11.2) як
на деяку операцію, що проводиться над
функцією, визначеною на ![]() Ця
операція називається операцією подвійного
інтегрування функції
Ця
операція називається операцією подвійного
інтегрування функції ![]() (або
(або ![]() )
за областю
,
а її результат – означеним інтегралом
від
)
за областю
,
а її результат – означеним інтегралом
від ![]() по
і
позначається так:
по
і
позначається так:
![]() .
.
Отже, об’єм циліндричного тіла
![]() .
(11.3)
.
(11.3)
Маса
тіла. Нехай
тепер в трьохвимірному просторі, де
визначена прямокутна декартова система
координат ![]() ,
задано тіло
(множина)
з неперервно розподіленою в ньому масою
з густиною розподілу
,
задано тіло
(множина)
з неперервно розподіленою в ньому масою
з густиною розподілу ![]() (
( ![]() ).
Потрібно визначити масу тіла
.
Розіб’ємо
на
частин
).
Потрібно визначити масу тіла
.
Розіб’ємо
на
частин ![]() об’єми
(трьохвимірні міри) яких ( в припущенні,
що вони існують) позначимо
об’єми
(трьохвимірні міри) яких ( в припущенні,
що вони існують) позначимо ![]() або
або ![]()
Виберемо
довільним чином в кожній частині точку ![]() і
тоді маса тіла
(по
аналогії із об’ємом циліндричного
тіла) дорівнює
і
тоді маса тіла
(по
аналогії із об’ємом циліндричного
тіла) дорівнює
|
|
|
|
Рис.11.2 Рис.11.3
![]() (11.4)
(11.4)
Знову
ж таки на вираз (11.4) можна дивитися як
на певну операцію над функцією ![]() ,
що задана в трьохвимірному просторі
.
,
що задана в трьохвимірному просторі
.
Ця операція на цей раз називається операцією потрійного інтегрування (за Ріманом 1)), а її результат – визначеним потрійним інтегралом, що позначається так:
![]()
Отже,
![]()
![]() (11.5)
(11.5)
До знаходження таких границь приводять не тільки задачі про визначення об’єму циліндричного тіла і знаходження маси, але й інші задачі.
Нижче
ми побачимо, що частина теорії кратного
інтегрування, зокрема, теореми існування
і теореми про аддитивні властивості
інтеграла, може бути викладена цілком
аналогічно як в одновимірному, так і
в ![]() вимірному
випадку. Проте в теорії кратних інтегралів
виникають певні труднощі, яких не було
в теорії звичайного означеного інтеграла.
вимірному
випадку. Проте в теорії кратних інтегралів
виникають певні труднощі, яких не було
в теорії звичайного означеного інтеграла.
Справа
в тому, що однократний інтеграл
Рімана 1) ми
визначали для дуже простої множини –
відрізку ![]() який
дробився знову на відрізки. Ніяких
труднощів у визначенні довжини
(одновимірної міри) відрізків не виникало.
Проте у випадку подвійних, потрійних
і, взагалі,
кратних
інтегралів область інтегрування
доводиться ділити (лініями, поверхнями,
гіперповерхнями) на частини з криволінійними
границями, і виникає питання визначення
поняття площі, об’єму або взагалі
вимірної
міри цих частин.
який
дробився знову на відрізки. Ніяких
труднощів у визначенні довжини
(одновимірної міри) відрізків не виникало.
Проте у випадку подвійних, потрійних
і, взагалі,
кратних
інтегралів область інтегрування
доводиться ділити (лініями, поверхнями,
гіперповерхнями) на частини з криволінійними
границями, і виникає питання визначення
поняття площі, об’єму або взагалі
вимірної
міри цих частин.
1) Б. Ріман (1826-1866) – німецький математик.
Поняття
про міру Жордана 1). В
двохвимірному випадку ми будемо мати
справу з обмеженими областями, що мають
гладку границю (рис. 11.2) або кусково-гладку
границю, що складається із кінцевого
числа гладких кусків (ліній). Ці області
в свою чергу доводиться ділити на
частини, що мають кусково-гладку границю.
Кожній такій області ![]() і
деяким іншим множинам можна привести
у відповідність додатне число
і
деяким іншим множинам можна привести
у відповідність додатне число ![]() яке
називається площею або двохвимірною
мірою Жордана . При цьому виконуються
такі властивості:
яке
називається площею або двохвимірною
мірою Жордана . При цьому виконуються
такі властивості:
1)
якщо ![]() прямокутник
з основою
прямокутник
з основою ![]() і
висотою
і
висотою ![]() то
то ![]()
2)
якщо ![]() і
і ![]() мають
міри
мають
міри ![]() то
то ![]()
3)
якщо область
розрізана
за допомогою кусково-гладкої кривої на
дві частини ![]() і
і ![]() то
то
![]()
Існують множини двохвимірної міри, що дорівнюють нулю, такі, як точка, відрізок, гладка або кусково-гладка крива.
В трьохвимірному випадку нас будуть цікавити області, що мають своєю границею кусково-гладкі поверхні. Куля, еліпсоїд, куб можуть служити прикладом таких поверхонь.
Поверхня називається гладкою, якщо в довільній її точці
можна провести дотичну площину, що неперервно змінюється разом з цією точкою. Поверхня називається кусково-гладкою, якщо її можна
розрізати на кінцеве число гладких кусків. По лінії розрізів дотичні площини можуть і не існувати.
Для
трьохвимірних обмежених областей
з
кусково-гладкими границями можна
визначити їх об’єм (трьохвимірну міру),
тобто додатне число ![]() ,
що задовольняє таким властивостям:
,
що задовольняє таким властивостям:
1)
якщо
прямокутний
паралелепіпед з ребрами ![]() то
то
![]()
2) якщо і мають міри то
3) якщо область розрізана за допомогою кусково-гладкої поверхні на дві частини і то
1) К. Жордан (1838-1922) – французький математик
Є множини трьохвимірної міри, що дорівнює нулю. Такими є точка, відрізок, плоский прямокутник, гладка або кусково-гладка поверхня.
Означення. Дамо тепер визначення кратного інтеграла, не розглядаючи задачі геометричного або фізичного змісту.
Нехай
в
вимірному
просторі ![]() задана
обмежена область
з
кусково-гладкою границею
задана
обмежена область
з
кусково-гладкою границею ![]() і
на
(або
на
і
на
(або
на ![]() )
задана функція
)
задана функція ![]() Розріжемо
довільним
чином на частини
Розріжемо
довільним
чином на частини ![]() ,
що перетинаються хіба що по своїх
границях, які будемо вважати
кусково-гладкими. Виберемо в кожній
частині
,
що перетинаються хіба що по своїх
границях, які будемо вважати
кусково-гладкими. Виберемо в кожній
частині ![]() по
довільній точці
по
довільній точці ![]() і
складемо суму
і
складемо суму
![]()
яку
будемо називати інтегральною сумою
Рімана функції ![]() що
відповідає даному розбиттю.
що
відповідає даному розбиттю.
Якщо
існує скінчена границя послідовності
інтегральних сум ![]() коли
максимальний діаметр частинних
множин
коли
максимальний діаметр частинних
множин
![]() (
)
і вона не залежить від вибору точок
в
,
а також не залежить від способів розбиття
області
,
то ця границя називається
кратним
інтегралом від функції
на
(або
по
).
Отже,
(
)
і вона не залежить від вибору точок
в
,
а також не залежить від способів розбиття
області
,
то ця границя називається
кратним
інтегралом від функції
на
(або
по
).
Отже,
![]() .
(11.6)
.
(11.6)
Зауваження. Чи
будемо ми обчислювати границю (11.6) для
області
,
чи для її замикання ![]() не
має значення, оскільки
не
має значення, оскільки ![]() де
де ![]() кусково-гладка
границя області
А
кусково-гладка границя області
має
вимірну
міру нуль
кусково-гладка
границя області
А
кусково-гладка границя області
має
вимірну
міру нуль ![]() .
.
КРАТНІ ІНТЕГРАЛИ

 Отже,
Отже, 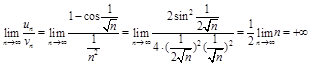 .
Друга ознака не дає відповіді на
запитання про збіжність, оскільки
.
Друга ознака не дає відповіді на
запитання про збіжність, оскільки 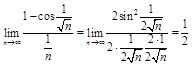 .
Оскільки
.
Оскільки